Oscilaciones forzadas (GIE)

Introducción

Un oscilador armónico amortiguado es aquel que, en adición a la fuerza recuperadora dada por la ley de Hooke, experimenta una fuerza de rozamiento viscoso proporcional a la velocidad.

$m{\vec {v}}=-k{\vec {r}}-\gamma {\vec {v}}\,$

Si este oscilador se mueve a lo largo de una recta, la segunda ley de Newton se reduce a

$ma=-kx-\gamma v\,$

donde $x$ es la elongación (distancia a la posición de equilibrio dada por la longitud natural).

Si este oscilador amortiguado se encuentra sometido a una fuerza externa adicional, en general dependiente del tiempo, se dice que el oscilador está forzado, siendo su ecuación de movimiento

$ma=-kx-\gamma v+F(t)\,$

De entre los posibles tipos de fuerza que se pueden aplicar, la más importante desde el punto de vista físico, es aquella que en sí misma es oscilante, esto es

$ma=-kx-\gamma v+F_{0}\cos(\omega t)\,$

donde la frecuencia de oscilación de la fuerza no tiene por qué coincidir con la frecuencia propia del oscilador armónico

$\omega \neq \omega _{0}={\sqrt {\frac {k}{m}}}$

El caso de una fuerza constante

El caso más sencillo de un oscilador forzado sería aquél sometido a una fuerza que no depende del tiempo $F=F_{0}$ ($\omega =0$). Este sería el caso de un muelle que cuelga verticalmente u del cual se cuelga una masa $m$, siendo su ecuación de movimiento

$m{\ddot {z}}+\gamma {\dot {z}}+kz=-mg$

Solución estacionaria

La solución en este caso es fácil de imaginar. Si de una balanza colgamos 1kg de plátanos, el muelle se estira y en el estado final se queda en reposo en una posición $z_{s}$ inferior a la inicial. En este estado equilibrio, al ser constante, las derivadas respecto al tiempo se anulan y nos queda

$z=z_{\mathrm {s} }\qquad {\dot {z}}=0\qquad {\ddot {z}}=0$

y sustituyendo obtenemos la posición de equilibrio

$m\cdot 0+\gamma \cdot 0+kz_{s}=-mg\qquad \Rightarrow \qquad z_{s}=-{\frac {mg}{k}}$

Esta estado estacionario es independiente de las condiciones iniciales. Ni la posición inicial ni la velocidad inicial aparecen en su expresión.

Solución transitoria

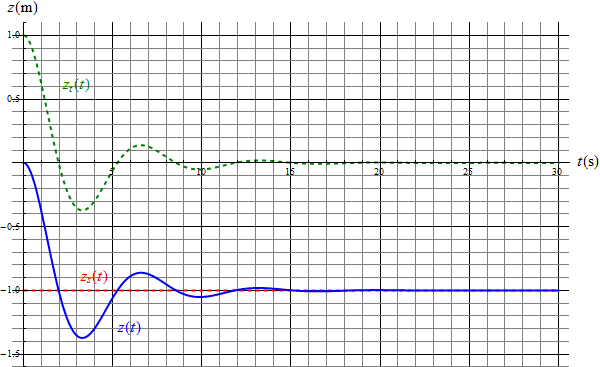
En el ejemplo de los plátanos que se cuelgan de la balanza, la experiencia nos muestra que la posición final no se alcanza instantáneamente, sino que la balanza oscila unas cuantas veces antes de detenerse. Se dice entonces que tenemos un proceso transitorio que representa el paso desde el estado inicial hasta el final.

Para describir matemáticamente el estado transitorio introducimos como variable la diferencia entre la posición instantánea y la de equilibrio

$s=z-z_{s}\qquad \Rightarrow \qquad z=s+z_{s}$

Teniendo en cuenta que la solución estacionaria es una de equilibrio

${\dot {z}}={\dot {s}}+{\dot {z}}_{s}={\dot {s}}\qquad \qquad {\ddot {z}}={\ddot {s}}+{\ddot {z}}_{s}={\ddot {s}}$

y sustituyendo en la ecuación del oscilador forzado queda

$m{\ddot {s}}+\gamma {\dot {s}}+ks+kz_{s}=-mg$

pero $kz_{s}=-mg$ así que esto se reduce a

$m{\ddot {s}}+\gamma {\dot {s}}+ks=0$

que es la ecuación del oscilador armónico amortiguado. Dependiendo del grado de amortiguamiento podemos tener un caso subamortiguado, crítico o sobreamortiguado. En cualquiera de los tres casos el comportamiento general es el mismo: la solución decae exponencialmente a cero. Este estado transitorio sí depende de las condiciones iniciales, que determinan las constantes de la solución.

Superposición

Según esto, la solución de un oscilador forzado se compone de dos partes:

$z(t)=z_{s}(t)+z_{t}(t)\,$

• Un estado transitorio inicial, $z_{t}(t)$, que depende de las condiciones iniciales y que decae exponencialmente.
• Un estado estacionario final, $z_{s}(t)$, que solo depende de la fuerza aplicada y no del estado inicial.

Este mismo principio se aplica al caso de que tengamos una fuerza oscilante en lugar de una constante.

Caso de una fuerza sinusoidal

Consideraremos ahora el caso de que la fuerza aplicada oscile sinusoidalmente.

$F(t)=F_{0}\cos(\omega t)\,$

Este caso contiene el anterior en el límite $\omega \to 0$.

Si escribimos la ecuación de movimiento expresando la velocidad y la aceleración como derivadas de la posición nos queda la ecuación

$m{\ddot {x}}+b{\dot {x}}+kx=F_{0}\cos(\omega t)$

Dividiendo por la masa podemos escribirla empleando los parámetros definidos al estudiar las oscilaciones amortiguadas

${\ddot {x}}+2\beta {\dot {x}}+\omega _{0}^{2}x={\frac {F_{0}}{m}}\cos(\omega t)$

donde

$\beta ={\frac {\gamma }{2m}}\qquad \qquad \omega _{0}={\sqrt {\frac {k}{m}}}$

El problema general consiste en determinar la elongación como función del tiempo, $x(t)$ para una posición y velocidad iniciales.

Como en el caso de una fuerza constante, la solución se puede escribir como suma de dos, una estacionaria y una transitoria, con la diferencia de que el estado estacionario ahora no es de reposo, sino de movimiento.

Cuando se aplica una fuerza oscilante a una masa atada a un muelle, el resultado es que la masa oscila. Lo hace además con la frecuencia de la señal aplicada. La solución puede escribirse entonces en la forma

$x=A\,\cos(\omega t+\varphi )$

siendo la amplitud de las oscilaciones y $\varphi$ el desfase con la fuerza aplicada (que no tiene por qué ser nulo; el que oscile con la misma frecuencia no quiere decir que esté sincronizado, puede ocurrir que cuando la fuerza sea máxima el desplazamiento sea nulo, por ejemplo). La amplitud y el desfase pueden cambiar mucho según sea la frecuencia de la fuerza aplicada, aunque esta sea siempre de la misma intensidad

Esto quiere decir que para conseguir una amplitud mayor no necesitamos aplicar una fuerza más intensa. Basta con elegir adecuadamente la frecuencia de su variación. Nuestro objetivo se reduce entonces a determinar $A$ y $\varphi$ como funciones de la intensidad de la fuerza aplicada y de su frecuencia.

La forma más sencilla de determinar estas constantes es mediante el uso de fasores. La fuerza aplicada puede escribirse, con ayuda de la fórmula de Euler, como

$F(t)=F_{0}\cos(\omega t)=\mathrm {Re} \left({\hat {F}}\mathrm {e} ^{\mathrm {j} \omega t}\right)$

donde

${\hat {F}}=F_{0}$

es el fasor, o amplitud compleja, de la fuerza. Es una cantidad compleja cuyo módulo nos da la amplitud de las oscilaciones ($F_{0}$ en este caso) y cuyo argumento nos da el desfase (nulo, en este caso).

En la solución estacionaria sinusoidal, la elongación admite una expresión análoga

$x(t)=A\cos(\omega t+\varphi )=\mathrm {Re} \left({\hat {x}}\mathrm {e} ^{\mathrm {j} \omega t}\right)$

donde ahora

${\hat {x}}=A\mathrm {e} ^{\mathrm {j} \varphi }\,$

Este fasor es una constante compleja contiene tanto la amplitud como la constante de fase de la solución, por lo que si determinamos el fasor, ya hemos resuelto nuestro problema.

La ventaja de usar fasores es que transforma las derivadas en multiplicaciones. La velocidad y la aceleración pueden expresarse también en forma fasorial, siendo sus amplitudes complejas

${\hat {v}}=\mathrm {j} \omega {\hat {x}}$    ${\hat {a}}=(\mathrm {j} \omega )^{2}{\hat {x}}=-\omega ^{2}{\hat {x}}$

Puesto que en la ecuación de movimiento

$a+2\beta v+\omega _{0}^{2}x={\frac {F_{0}}{m}}\cos(\omega t)\,$

todas las cantidades ($F$, $x$, $v$ y $a$) oscilan con la misma frecuencia, podemos escribirla como una relación entre fasores

${\hat {a}}+2\beta {\hat {v}}+\omega _{0}^{2}{\hat {x}}={\frac {\hat {F}}{m}}$

Sustituyendo los fasores de la velocidad y la aceleración nos queda

$-\omega ^{2}{\hat {x}}+2\mathrm {j} \beta \omega {\hat {x}}+\omega _{0}^{2}{\hat {x}}={\frac {\hat {F}}{m}}$

Esta es una ecuación algebraica de la cual es inmediato despejar el fasor de la elongación

${\hat {x}}={\frac {{\hat {F}}/m}{(\omega _{0}^{2}-\omega ^{2})+2\mathrm {j} \omega \beta }}$

Amplitud

La amplitud de las oscilaciones la hallamos como el módulo del fasor. A su vez, el módulo de un cociente de números complejos es el cociente de los módulos, por lo que

$A=\left|{\hat {x}}\right|={\frac {F_{0}/m}{\sqrt {(\omega _{0}^{2}-\omega ^{2})^{2}+4\beta ^{2}\omega ^{2})}}}$

Desfase

El desfase entre las oscilaciones de la elongación y la fuerza aplicada lo da el argumento del fasor

$\phi =\mathrm {arg} ({\hat {x}})=-\mathrm {arctg} \left({\frac {2\beta \omega b}{\omega _{0}^{2}-\omega ^{2}}}\right)$

Dependencia con la frecuencia

Los fasores de la posición y de la velocidad (y por tanto sus amplitudes y desfases) son funciones de la frecuencia, lo cual quiere decir que la respuesta de un oscilador a una fuerza que varía sinusoidalmente no depende solo de la magnitud de la fuerza. Una fuerza pequeña puede tener un gran efecto, si la frecuencia es adecuada, o, por el contrario, una gran fuerza aplicada puede no tener efecto apreciable. Dependiendo del sistema que se esté estudiando, puede interesar una cosa o la otra. Así, para un receptor de radio, interesa que se amplifiquen las frecuencias de las señales de la frecuencia deseada, y no las del resto, esto se consigue ajustando principalmente dos parámetros, la frecuencia propia del oscilador y su coeficiente de amortiguamiento, definidos por

$\omega _{0}={\sqrt {\frac {k}{m}}}$    $\beta ={\frac {b}{2m}}$

Amplitud

La amplitud de la elongación, en términos de la frecuencia propia y del factor de amortiguamiento queda en la forma

$A(\omega )={\frac {F_{0}/m}{\sqrt {(\omega _{0}^{2}-\omega ^{2})^{2}+4\beta ^{2}\omega ^{2}}}}$

Bajas frecuencias

Cuando $\omega \to 0$, la amplitud de las oscilaciones tiende a

$A(\omega )\simeq {\frac {F_{0}/m}{\omega _{0}^{2}}}={\frac {F_{0}}{k}}\qquad (\omega \ll \omega _{0})$

que es el comportamiento que uno obtiene para una fuerza no oscilante, como el peso, para el cual la frecuencia sería estrictamente nula.

Altas frecuencias

Si $\omega \to \infty$ Para frecuencias altas la amplitud tiende a cero

$A(\omega )\simeq 0\qquad (\omega \gg \omega _{0})$

Esto quiere decir que si un oscilador lo excitamos mediante una fuerza cuya frecuencia sea mucho mayor que la propia del oscilador, éste prácticamente no se ve afectado.

Para valores intermedios de la frecuencia, de valor comparable a la frecuencia propia $\omega _{0}$, podemos tener un máximo de amplitud o no tenerlo dependiendo del grado de amortiguamiento. La amplitud es máxima cuando lo que hay dentro de la raíz del denominador es mínimo, lo cual ocurre para

$\omega _{\mathrm {max} }={\sqrt {\omega _{0}^{2}-2\beta ^{2}}}$

como se comprueba sin más que derivar el radicando e igualar a cero. Gráficamente obtenemos una curva con un máximo que es más agudo cuanto menor sea el coeficiente de amortiguamiento $\beta$. Para representarlo conviene emplear una escala logarítmica para las frecuencias ya que de esta forma se puede barrer un rango más amplio sin comprimir la gráfica.

    

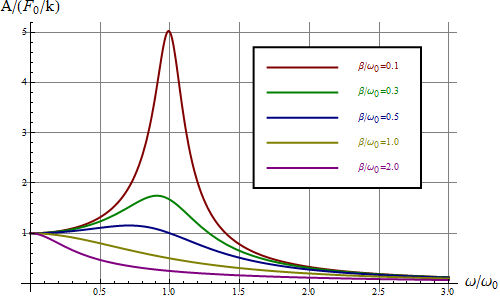
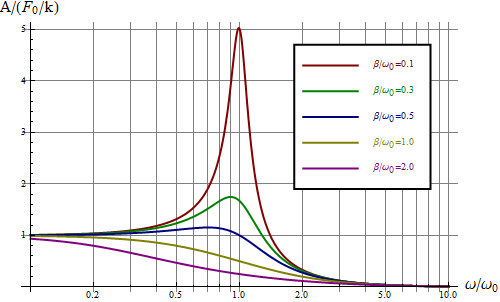
Cuando existe este máximo (que puede ser muy destacado) se dice que el sistema posee una resonancia. Físicamente este resultado nos dice que ajustando la frecuencia de la fuerza aplicada podemos obtener una respuesta de gran amplitud (infinita en el caso sin rozamiento). Por ejemplo, para el caso $\beta =0.1\omega _{0}$ obtenemos que las amplitudes de las oscilaciones resultantes es 5 veces lo que se estira en el caso estático. La altura del máximo es

$A_{\mathrm {max} }={\frac {F_{0}/m}{2\beta {\sqrt {\omega _{0}^{2}-\beta ^{2}}}}}$

Para valores de $\beta$ pequeños la posición del máximo ocurre aproximadamente a la frecuencia propia (por lo que también se la llama frecuencia de resonancia) y la altura es inversamente proporcional al amortiguamiento

$\omega _{\mathrm {max} }\simeq \omega _{0}\qquad \qquad A_{\mathrm {max} }\simeq {\frac {F_{0}/m}{2\beta \omega _{0}}}\qquad \qquad (\beta \ll \omega _{0})$

Este efecto puede ser deseable (es la base de los sintonizadores de radio, por ejemplo), pero también puede ser indeseado. A menudo es la causa de los ruidos molestos que producen ordenadores y otros aparatos, por vibraciones de los ventiladores y otras partes móviles. La razón de que muchos de estos ruidos desaparezcan cuando se golpea el aparato es porque al hacerlo se modifica la frecuencia propia y el sistema deja de estar en una resonancia.

Una resonancia de gran amplitud puede tener efectos dramáticos, provocando la fractura de partes del sistema. El caso más famoso de este fenómeno es el colapso del puente de Tacoma Narrows en Washington (USA).

(vídeo de la catástrofe en Youtube).

Fase

El movimiento del oscilador no tiene por qué ir en fase con la fuerza. Es posible que para una frecuencia dada cuando la fuerza vaya hacia abajo la partícula se mueva hacia arriba (ya que la fuerza nos da la aceleración, pero no directamente la posición).

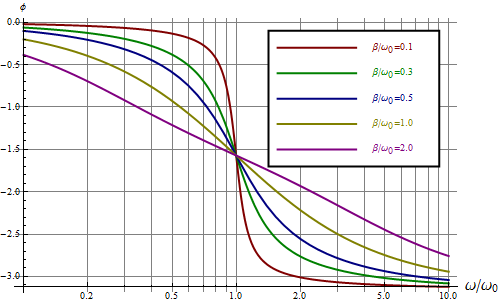
La diferencia de fase lo hallamos a partir del argumento del fasor. Usando la fórmula para el argumento de un cociente de números complejos

$\varphi =\mathrm {arg} ({\hat {x}})=\mathrm {arg} (F_{0}/m)-\mathrm {arg} \left((\omega _{0}^{2}-\omega ^{2})+4\mathrm {j} \beta \omega \right)=-\mathrm {arctg} \left({\frac {2\beta \omega }{\omega _{0}^{2}-\omega ^{2}}}\right)$

Para frecuencias bajas ($\omega \to 0$) se obtiene desfase 0. Esto corresponde a que si la fuerza es constante en un sentido (por ejemplo, el peso, hacia abajo), el resultado es un desplzamiento constante en el mismo sentido. Justo en la resonancia el desfase es de $\pi /2$, es decir, cuando la fuerza es máxima el desplazamiento es nulo y viceversa. Para frecuencias grandes el desfase tiende a $\pi$ lo que implica que el desplazamiento va en sentido contrario a la fuerza.

Velocidad

A menudo es más interesante conocer la velocidad del oscilador forzado, más que su posición. La velocidad también se puede expresar en forma fasorial

$v(t)=V\cos(\omega t+\theta )=\mathrm {Re} \left({\hat {v}}\mathrm {e} ^{\mathrm {j} \omega t}\right)\qquad \qquad {\hat {v}}=V\mathrm {e} ^{\mathrm {j} \theta }$

Obtenemos el fasor de la velocidad multiplicando el de la elongación por $\mathrm {j} \omega$

${\hat {v}}=\mathrm {j} \omega {\hat {x}}={\frac {\mathrm {j} \omega {\hat {F}}/m}{(\omega _{0}-\omega ^{2})+2\mathrm {j} \beta \omega }}$

Dividiendo en el numerador y el denominador por $\mathrm {j} \omega$

${\hat {v}}={\frac {{\hat {F}}/m}{2\beta +\mathrm {j} (\omega -\omega _{0}^{2}/\omega )}}$

Amplitud

La amplitud de las oscilaciones de la velocidad es

$V(\omega )=|{\hat {v}}|={\frac {F_{0}/m}{\sqrt {4\beta ^{2}+(\omega -\omega _{0}^{2}/\omega )^{2}}}}$

De nuevo tenemos una función dependiente de la frecuencia.

Bajas frecuencias

Cuando $\omega \to 0$, el término $\omega _{0}^{2}/\omega$ tiende a infinito y la amplitud se va a cero. Esto quiere decir que para una fuerza que varía muy lentamente, el oscilador se mueve muy lentamente, de forma que en todo momento está casi en la posición de equilibrio calculada anteriormente.

Altas frecuencias

Cuando $\omega \to \infty$, de nuevo el dernominador tiende a infinito y la amplitud se va de nuevo a cero. Esto quiere decir que para una fuerza que varía muy rápidamente, la inercia del oscilador le impide responder y este se limita a vibrar ligeramente alrededor de su posición de equilibrio $x=0$.

Resonancia

En la raíz que aparece en la amplitud hay una suma de dos términos positivos. El primero no se anula nunca, pero el segundo se hace cero si

$\omega ={\frac {\omega _{0}^{2}}{\omega }}$ ⇒ $\omega =\omega _{0}={\sqrt {\frac {k}{m}}}$

esto es, si la frecuencia de la fuerza aplicada coincide con la frecuencia propia del oscilador, la amplitud de las oscilaciones en la velocidad es máxima. Vemos que, a diferencia de lo que ocurre con la elongación, el máximo en la amplitud de la velocidad está siempre centrado en la misma frecuencia (conocida como frecuencia de resonancia). El valor máximo de esta amplitud será

$V_{\mathrm {max} }=V(\omega _{0})={\frac {F_{0}}{\gamma }}$

que tiende a infinito cuando el rozamiento se hace nulo.

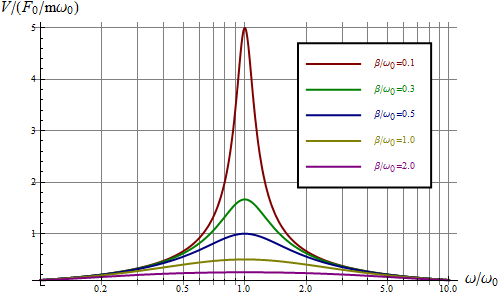
Si se emplea una escala logarítmica para las frecuencias el resultado es una curva simétrica alrededor de la frecuencia de resonancia.

Desfase

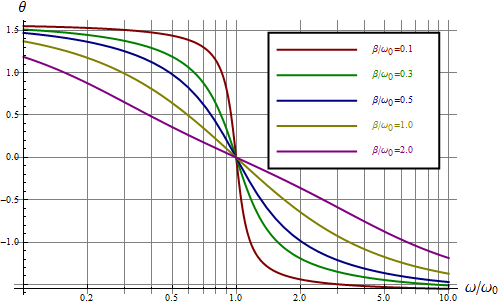
El desfase entre las oscilaciones de la velocidad y la fuerza aplicada es igual a

$\theta =\mathrm {arg} ({\hat {v}})=\mathrm {arctg} \left({\frac {\omega _{0}^{2}-\omega ^{2}}{2\beta \omega }}\right)$

La curva es igual al desfase de la elongación, pero desplazada en $\pi /2$. En la frecuencia de resonancia la velocidad y la fuerza van en fase

Energía y potencia

Al existir una fuerza de rozamiento, la energía se está transformando continuamente en calor. Puesto que la energía almacenada, en promedio, se conserva, esta energía que se pierde debe ser aportada regularmente por un agente externo, en este caso, la fuerza aplicada sobre la partícula.

La potencia con la que se disipa la energía es

$P_{d}=P_{\mathrm {nc} }=\mathbf {F} _{nc}\cdot \mathbf {v} =-\gamma v^{2}$

Sustituyendo la velocidad como función del tiempo

$P_{d}=-\gamma V^{2}\cos ^{2}(\omega t+\theta )$

La energía total disipada durante un periodo será, aplicando que

$\int _{0}^{2\pi }\cos ^{2}(x)\mathrm {d} x=\pi$

igual a

$W_{d}=\int _{0}^{P}P_{\mathrm {nc} }\,\mathrm {d} t=-{\frac {\pi \gamma V^{2}}{\omega }}$

Sustituyendo el valor de la amplitud en la velocidad

$W_{d}(\omega )=-{\frac {2\pi \beta \omega F_{0}^{2}/m}{(\omega _{0}^{2}-\omega ^{2})^{2}+4\beta ^{2}\omega ^{2}}}$

siendo la potencia promedio

$\langle P_{d}\rangle ={\frac {W_{d}}{T}}=-{\frac {\beta \omega ^{2}F_{0}^{2}/m}{(\omega _{0}^{2}-\omega ^{2})^{2}+4\beta ^{2}\omega ^{2}}}$

Representando gráficamente esta potencia promedio disipada como función de la frecuencia se obtiene de nuevo una curva con un máximo en la frecuencia de resonancia

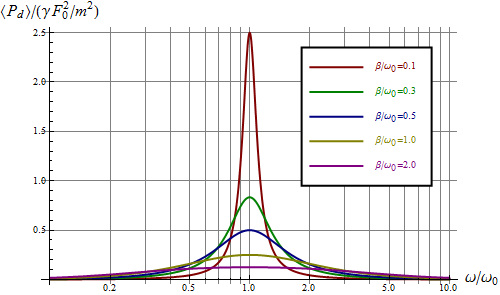
Esto quiere decir que la frecuencia de resonancia es aquella en la que el sistema absorbe más energía de la fuerza aplicada, es decir, es la forma más efectiva de transmitir energía a un sistema. Si se emplea una frecuencia diferente el proceso ya no es tan eficiente.

En un ejemplo sencillo, esto nos está diciendo que si queremos impulsar un columpio, por ejemplo, debemos aplicar una fuerza oscilante cuya frecuencia debe ser lo más parecida posible a la propia del oscilador. No sirve de nada que unas veces empujemos el columpio cuando se va a lejando de nosotros y otras cuando se está acercando. Hay que hacerlo siempre cuando se está alejando. De esta forma se le comunica el máximo de energía posible y la amplitud de las oscilaciones resultantes es la mayor posible.

Factor de calidad

Ancho de banda

El factor de calidad, $Q$, de un oscilador mide cómo de agudo es el pico de una resonancia. Se define, en términos de la energía, como

$Q=2\pi {\frac {\mbox{Energia almacenada promedio}}{\mbox{Energia disipada en un periodo}}}=2\pi {\frac {\left\langle E\right\rangle }{|W_{d}|}}$

donde las cantidades se evalúan en la frecuencia de resonancia $\omega _{0}$. Calculando y sustituyendo los valores de la energía almacenada y de la disipada queda

$Q={\frac {\sqrt {km}}{\gamma }}$

Gráficamente, para resonancias muy agudas, el factor de calidad es inversamente proporcional al ancho de banda, que es la anchura del pico de la curva de la amplitud como función de la frecuencia, medida a media altura

$Q\simeq {\frac {\omega _{0}}{\Delta \omega }}$