No Boletín - Eje con un disco por encima y otro por debajo (Ex.Ene/13)
Enunciado
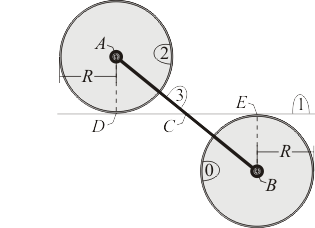
Los sólidos "2" y "0" son dos discos de radio vinculados entre sí al hallarse sus centros articulados, respectivamente, a los dos extremos de la varilla rígida (sólido "3"). Ambos discos están rodando sin deslizar sobre un eje horizontal (sólido "1") simultánea y permanentemente, aunque -tal como muestra la figura- el disco "2" lo está haciendo por encima del eje, mientras que el disco "0" lo está haciendo por debajo del mismo.
- ¿Dónde se halla el centro instantáneo de rotación ?
- ¿Qué tipo de movimiento es el {31}?
Solución
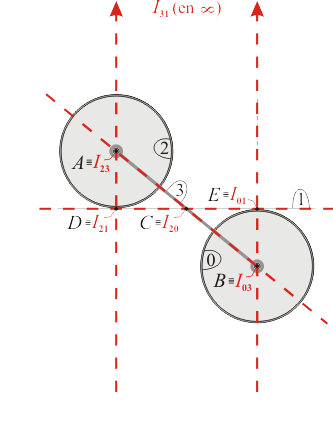
El disco "2" se halla articulado en su centro al extremo de la varilla "3". Por tanto, dicho punto es un punto fijo (centro permanente de rotación) en el movimiento {23}:
El disco "0" se halla articulado en su centro al extremo de la varilla "3". Por tanto, dicho punto es un punto fijo (centro permanente de rotación) en el movimiento {03}:
El disco "2" rueda sin deslizar por la parte superior del eje horizontal "1". La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {21} coincide con el punto de contacto entre dicho disco y el eje:
El disco "0" rueda sin deslizar por la parte inferior del eje horizontal "1". La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {01} coincide con el punto de contacto entre dicho disco y el eje:
Aplicando dos veces el teorema de los tres centros (una vez para la terna de sólidos "2"-"0"-"1", y otra vez para la terna "2"-"0"-"3"), llegamos a la conclusión de que el centro instantáneo de rotación del movimiento {20} se halla en la intersección de las rectas y , es decir, coincide con el punto de la figura del enunciado:
Aplicando dos veces el teorema de los tres centros (una vez para la terna de sólidos "2"-"3"-"1", y otra vez para la terna "0"-"3"-"1"), llegamos a la conclusión de que el centro instantáneo de rotación del movimiento {31} se halla en la intersección de las rectas y . Y como estas dos rectas son paralelas verticales, quiere eso decir que el CIR{31} se halla en el infinito en dirección vertical:
Lo cual nos está indicando que el movimiento {31} es una traslación horizontal.















