No Boletín - Cuestión sobre posiciones de equilibrio (Ex.Ene/12)

Enunciado

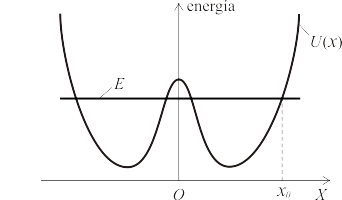
Una partícula se mueve en el eje $OX\,$ bajo la acción de una fuerza conservativa. La función energía potencial $U(x)\,$ y el nivel de energía mecánica $E\,$ de la partícula son los representados en la gráfica adjunta. En el instante inicial la partícula se halla en la posición $x=x_{0}\,$, la cual se observa que corresponde a uno de los puntos de corte de $E\,$ y $U(x)\,$.

¿Por cuántas posiciones de equilibrio distintas pasará sin detenerse la partícula en su movimiento?

Solución

En el caso de un movimiento unidimensional conservativo, las posiciones de equilibrio son aquellas para las cuales existen extremos locales de la función energía potencial, es decir, aquellas posiciones para las que la partícula alcanza un mínimo (eq. estable) o un máximo (eq. inestable) de energía potencial. Así pues, para la curva de potencial del enunciado, detectamos en principio la existencia de tres posiciones de equilibrio (dos estables y una inestable).

Ahora bien, que una posición de equilibrio exista no implica que la partícula vaya a tener acceso a ella. Esto va a depender de las condiciones iniciales del movimiento o, dicho de otro modo, del nivel concreto de energía mecánica que tenga la partícula (recuérdese que el nivel de energía mecánica es constante y se calcula a partir de las condiciones iniciales). En el caso que nos ocupa, observamos que el nivel de energía mecánica está por debajo del máximo local de energía potencial (lo cual convierte a la posición de equilibrio inestable en inaccesible para la partícula), pero por encima de los dos mínimos simétricos de la citada función de energía potencial. Por tanto, las dos posiciones de equilibrio estable quedan dentro de sendas regiones "permitidas" para la partícula. Pero nótese que esas dos regiones "permitidas" son dos pozos de potencial separados por una barrera infranqueable. En efecto, el máximo local de energía potencial, que resulta inaccesible con el nivel de energía mecánica que tiene la partícula, se encuentra separando esas dos regiones "permitidas". Por la posición inicial dada $x=x_{0}\,$, sabemos que la partícula se halla en el instante inicial en el pozo de la derecha de la gráfica. Pues bien, de dicho pozo no podrá escapar y, por tanto, oscilará indefinidamente alrededor de la única posición de equilibrio que queda dentro del mismo.

En definitiva, la respuesta a la pregunta del enunciado es UNA.

Nota: Esta cuestión se planteó en examen tipo-test y las respuestas propuestas (a elegir una) fueron: NINGUNA, UNA, DOS y TRES.