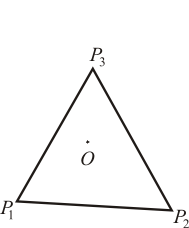
Enunciado Sea
P
1
P
2
P
3
{\displaystyle P_{1}P_{2}P_{3}\,}
A
{\displaystyle A\,}
O
{\displaystyle O\,}
¿Cuál de las siguientes igualdades es falsa?
(1)
|
P
1
P
2
→
×
P
2
P
3
→
+
P
2
P
3
→
×
P
3
P
1
→
+
P
3
P
1
→
×
P
1
P
2
→
|
=
6
A
{\displaystyle \left|{\overrightarrow {P_{1}P_{2}}}\times {\overrightarrow {P_{2}P_{3}}}+{\overrightarrow {P_{2}P_{3}}}\times {\overrightarrow {P_{3}P_{1}}}+{\overrightarrow {P_{3}P_{1}}}\times {\overrightarrow {P_{1}P_{2}}}\right|=6A\,}
(2)
|
O
P
1
→
×
P
1
P
2
→
+
O
P
2
→
×
P
2
P
3
→
+
O
P
3
→
×
P
3
P
1
→
|
=
2
A
{\displaystyle \left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{1}P_{2}}}+{\overrightarrow {OP_{2}}}\times {\overrightarrow {P_{2}P_{3}}}+{\overrightarrow {OP_{3}}}\times {\overrightarrow {P_{3}P_{1}}}\right|=2A\,}
(3)
|
O
P
1
→
×
P
1
P
2
→
+
O
P
1
→
×
P
2
P
3
→
+
O
P
1
→
×
P
3
P
1
→
|
=
0
{\displaystyle \left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{1}P_{2}}}+{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{2}P_{3}}}+{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{3}P_{1}}}\right|=0\,}
(4)
|
O
P
1
→
×
O
P
2
→
+
O
P
2
→
×
O
P
3
→
+
O
P
3
→
×
O
P
1
→
|
=
3
A
{\displaystyle \left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {OP_{2}}}+{\overrightarrow {OP_{2}}}\times {\overrightarrow {OP_{3}}}+{\overrightarrow {OP_{3}}}\times {\overrightarrow {OP_{1}}}\right|=3A\,}
Solución Empezamos examinando la igualdad (3), en la cual podemos sacar el vector
O
P
1
→
{\displaystyle {\overrightarrow {OP_{1}}}\,}
|
O
P
1
→
×
P
1
P
2
→
+
O
P
1
→
×
P
2
P
3
→
+
O
P
1
→
×
P
3
P
1
→
|
=
|
O
P
1
→
×
(
P
1
P
2
→
+
P
2
P
3
→
+
P
3
P
1
→
)
|
=
|
O
P
1
→
×
P
1
P
1
→
|
=
{\displaystyle \left|\,{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{1}P_{2}}}+{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{2}P_{3}}}+{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{3}P_{1}}}\right|=\left|\,{\overrightarrow {OP_{1}}}\times \left({\overrightarrow {P_{1}P_{2}}}+{\overrightarrow {P_{2}P_{3}}}+{\overrightarrow {P_{3}P_{1}}}\right)\right|=\left|\,{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{1}P_{1}}}\right|=}
=
|
O
P
1
→
×
0
→
|
=
|
0
→
|
=
0
{\displaystyle =\left|\,{\overrightarrow {OP_{1}}}\times {\vec {0}}\,\right|=\left|\,{\vec {0}}\,\right|=0}
Por tanto, la igualdad (3) es correcta.
Un detalle importante que conviene observar en las igualdades (1), (2) y (4) es que todos los productos vectoriales que aparecen en ellas tienen la misma dirección (perpendicular al plano del triángulo) y el mismo sentido (saliente). Nótese que, sólo cuando se suman vectores que tienen la misma dirección y el mismo sentido, se puede igualar el módulo de la suma con la suma de los módulos. También vamos a utilizar la propiedad geométrica del producto vectorial que dice que "el módulo del producto vectorial de dos vectores es igual al doble del área del triángulo que tiene a ambos vectores como dos de sus lados".
Procedamos a examinar la igualdad (1):
|
P
1
P
2
→
×
P
2
P
3
→
+
P
2
P
3
→
×
P
3
P
1
→
+
P
3
P
1
→
×
P
1
P
2
→
|
=
|
P
1
P
2
→
×
P
2
P
3
→
|
⏟
2
A
r
e
a
(
P
1
P
2
P
3
)
+
|
P
2
P
3
→
×
P
3
P
1
→
|
⏟
2
A
r
e
a
(
P
1
P
2
P
3
)
+
|
P
3
P
1
→
×
P
1
P
2
→
|
⏟
2
A
r
e
a
(
P
1
P
2
P
3
)
=
{\displaystyle \left|{\overrightarrow {P_{1}P_{2}}}\times {\overrightarrow {P_{2}P_{3}}}+{\overrightarrow {P_{2}P_{3}}}\times {\overrightarrow {P_{3}P_{1}}}+{\overrightarrow {P_{3}P_{1}}}\times {\overrightarrow {P_{1}P_{2}}}\right|=\underbrace {\left|{\overrightarrow {P_{1}P_{2}}}\times {\overrightarrow {P_{2}P_{3}}}\right|} _{2\,\mathrm {Area} (P_{1}P_{2}P_{3})}+\underbrace {\left|{\overrightarrow {P_{2}P_{3}}}\times {\overrightarrow {P_{3}P_{1}}}\right|} _{2\,\mathrm {Area} (P_{1}P_{2}P_{3})}+\underbrace {\left|{\overrightarrow {P_{3}P_{1}}}\times {\overrightarrow {P_{1}P_{2}}}\right|} _{2\,\mathrm {Area} (P_{1}P_{2}P_{3})}=}
=
2
A
+
2
A
+
2
A
=
6
A
{\displaystyle =2A\,+\,2A\,+\,2A=6A}
Por tanto, la igualdad (1) es correcta.
Procedamos a examinar la igualdad (2):
|
O
P
1
→
×
P
1
P
2
→
+
O
P
2
→
×
P
2
P
3
→
+
O
P
3
→
×
P
3
P
1
→
|
=
|
O
P
1
→
×
P
1
P
2
→
|
⏟
2
A
r
e
a
(
O
P
1
P
2
)
+
|
O
P
2
→
×
P
2
P
3
→
|
⏟
2
A
r
e
a
(
O
P
2
P
3
)
+
|
O
P
3
→
×
P
3
P
1
→
|
⏟
2
A
r
e
a
(
O
P
3
P
1
)
⏟
2
[
A
r
e
a
(
O
P
1
P
2
)
+
A
r
e
a
(
O
P
2
P
3
)
+
A
r
e
a
(
O
P
3
P
1
)
]
⏟
2
A
r
e
a
(
P
1
P
2
P
3
)
=
2
A
{\displaystyle \left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{1}P_{2}}}+{\overrightarrow {OP_{2}}}\times {\overrightarrow {P_{2}P_{3}}}+{\overrightarrow {OP_{3}}}\times {\overrightarrow {P_{3}P_{1}}}\right|=\underbrace {\underbrace {\underbrace {\left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{1}P_{2}}}\right|} _{2\,\mathrm {Area} (OP_{1}P_{2})}+\underbrace {\left|{\overrightarrow {OP_{2}}}\times {\overrightarrow {P_{2}P_{3}}}\right|} _{2\,\mathrm {Area} (OP_{2}P_{3})}+\underbrace {\left|{\overrightarrow {OP_{3}}}\times {\overrightarrow {P_{3}P_{1}}}\right|} _{2\,\mathrm {Area} (OP_{3}P_{1})}} _{2\,[Area(OP_{1}P_{2})\,+\,Area(OP_{2}P_{3})\,+\,Area(OP_{3}P_{1})]}} _{2\,\mathrm {Area} (P_{1}P_{2}P_{3})}=2A}
Por tanto, la igualdad (2) es correcta.
Procedamos a examinar la igualdad (4):
|
O
P
1
→
×
O
P
2
→
+
O
P
2
→
×
O
P
3
→
+
O
P
3
→
×
O
P
1
→
|
=
|
O
P
1
→
×
O
P
2
→
|
⏟
2
A
r
e
a
(
O
P
1
P
2
)
+
|
O
P
2
→
×
O
P
3
→
|
⏟
2
A
r
e
a
(
O
P
2
P
3
)
+
|
O
P
3
→
×
O
P
1
→
|
⏟
2
A
r
e
a
(
O
P
3
P
1
)
⏟
2
[
A
r
e
a
(
O
P
1
P
2
)
+
A
r
e
a
(
O
P
2
P
3
)
+
A
r
e
a
(
O
P
3
P
1
)
]
⏟
2
A
r
e
a
(
P
1
P
2
P
3
)
=
2
A
≠
3
A
{\displaystyle \left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {OP_{2}}}+{\overrightarrow {OP_{2}}}\times {\overrightarrow {OP_{3}}}+{\overrightarrow {OP_{3}}}\times {\overrightarrow {OP_{1}}}\right|=\underbrace {\underbrace {\underbrace {\left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {OP_{2}}}\right|} _{2\,\mathrm {Area} (OP_{1}P_{2})}+\underbrace {\left|{\overrightarrow {OP_{2}}}\times {\overrightarrow {OP_{3}}}\right|} _{2\,\mathrm {Area} (OP_{2}P_{3})}+\underbrace {\left|{\overrightarrow {OP_{3}}}\times {\overrightarrow {OP_{1}}}\right|} _{2\,\mathrm {Area} (OP_{3}P_{1})}} _{2\,[Area(OP_{1}P_{2})\,+\,Area(OP_{2}P_{3})\,+\,Area(OP_{3}P_{1})]}} _{2\,\mathrm {Area} (P_{1}P_{2}P_{3})}=2A\neq 3A}
Por tanto, la afirmación (4) es la que es FALSA.












![{\displaystyle \left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{1}P_{2}}}+{\overrightarrow {OP_{2}}}\times {\overrightarrow {P_{2}P_{3}}}+{\overrightarrow {OP_{3}}}\times {\overrightarrow {P_{3}P_{1}}}\right|=\underbrace {\underbrace {\underbrace {\left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {P_{1}P_{2}}}\right|} _{2\,\mathrm {Area} (OP_{1}P_{2})}+\underbrace {\left|{\overrightarrow {OP_{2}}}\times {\overrightarrow {P_{2}P_{3}}}\right|} _{2\,\mathrm {Area} (OP_{2}P_{3})}+\underbrace {\left|{\overrightarrow {OP_{3}}}\times {\overrightarrow {P_{3}P_{1}}}\right|} _{2\,\mathrm {Area} (OP_{3}P_{1})}} _{2\,[Area(OP_{1}P_{2})\,+\,Area(OP_{2}P_{3})\,+\,Area(OP_{3}P_{1})]}} _{2\,\mathrm {Area} (P_{1}P_{2}P_{3})}=2A}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/01dc4280a89dd570071f712e5d71eda1f5f3906b)
![{\displaystyle \left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {OP_{2}}}+{\overrightarrow {OP_{2}}}\times {\overrightarrow {OP_{3}}}+{\overrightarrow {OP_{3}}}\times {\overrightarrow {OP_{1}}}\right|=\underbrace {\underbrace {\underbrace {\left|{\overrightarrow {OP_{1}}}\times {\overrightarrow {OP_{2}}}\right|} _{2\,\mathrm {Area} (OP_{1}P_{2})}+\underbrace {\left|{\overrightarrow {OP_{2}}}\times {\overrightarrow {OP_{3}}}\right|} _{2\,\mathrm {Area} (OP_{2}P_{3})}+\underbrace {\left|{\overrightarrow {OP_{3}}}\times {\overrightarrow {OP_{1}}}\right|} _{2\,\mathrm {Area} (OP_{3}P_{1})}} _{2\,[Area(OP_{1}P_{2})\,+\,Area(OP_{2}P_{3})\,+\,Area(OP_{3}P_{1})]}} _{2\,\mathrm {Area} (P_{1}P_{2}P_{3})}=2A\neq 3A}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9d1d8e987d28e5a2da9518a634f55b5c4b8d9ddc)