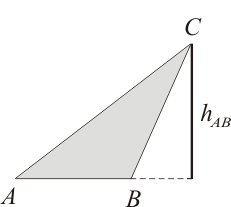
Enunciado Sea un triángulo
A
B
C
{\displaystyle \,ABC\,}
h
A
B
{\displaystyle \,h_{AB}\,}
A
B
{\displaystyle \,AB\,}
(NOTA : sólo una de las cuatro opciones es correcta).
(1)
h
A
B
=
|
(
A
B
→
×
A
C
→
)
×
A
B
→
|
|
A
B
→
|
2
{\displaystyle h_{AB}=\displaystyle {\frac {|({\overrightarrow {AB}}\times {\overrightarrow {AC}})\times {\overrightarrow {AB}}\,|}{|{\overrightarrow {AB}}\,|^{2}}}\,}
(2)
h
A
B
=
|
(
A
C
→
⋅
A
B
→
)
A
C
→
|
|
A
C
→
|
2
{\displaystyle h_{AB}=\displaystyle {\frac {|({\overrightarrow {AC}}\cdot {\overrightarrow {AB}})\,{\overrightarrow {AC}}\,|}{|{\overrightarrow {AC}}\,|^{2}}}\,}
(3)
h
A
B
=
|
(
A
C
→
×
A
B
→
)
×
A
C
→
|
|
A
C
→
|
2
{\displaystyle h_{AB}=\displaystyle {\frac {|({\overrightarrow {AC}}\times {\overrightarrow {AB}})\times {\overrightarrow {AC}}\,|}{|{\overrightarrow {AC}}\,|^{2}}}\,}
(4)
h
A
B
=
|
(
A
B
→
⋅
A
C
→
)
A
B
→
|
|
A
B
→
|
2
{\displaystyle h_{AB}=\displaystyle {\frac {|({\overrightarrow {AB}}\cdot {\overrightarrow {AC}})\,{\overrightarrow {AB}}\,|}{|{\overrightarrow {AB}}\,|^{2}}}\,}
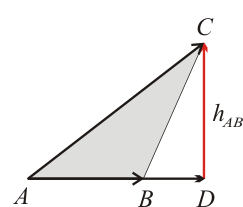
Solución Utilizando una fórmula deducida en la teoría, descomponemos el vector
A
C
→
{\displaystyle {\overrightarrow {AC}}\,}
A
B
→
{\displaystyle {\overrightarrow {AB}}\,}
A
D
→
{\displaystyle {\overrightarrow {AD}}\,}
A
B
→
{\displaystyle {\overrightarrow {AB}}\,}
D
C
→
{\displaystyle {\overrightarrow {DC}}\,}
A
C
→
=
(
A
B
→
⋅
A
C
→
)
A
B
→
|
A
B
→
|
2
⏟
A
D
→
+
(
A
B
→
×
A
C
→
)
×
A
B
→
|
A
B
→
|
2
⏟
D
C
→
{\displaystyle {\overrightarrow {AC}}=\underbrace {\displaystyle {\frac {({\overrightarrow {AB}}\cdot {\overrightarrow {AC}}\,){\overrightarrow {AB}}}{|{\overrightarrow {AB}}\,|^{2}}}} _{\overrightarrow {AD}}\,+\,\underbrace {\displaystyle {\frac {({\overrightarrow {AB}}\times {\overrightarrow {AC}}\,)\times {\overrightarrow {AB}}}{|{\overrightarrow {AB}}\,|^{2}}}} _{\overrightarrow {DC}}}
Resulta obvio que la longitud de la altura buscada coincide precisamente con el módulo del vector perpendicular a
A
B
→
{\displaystyle {\overrightarrow {AB}}\,}
h
A
B
=
|
D
C
→
|
=
|
(
A
B
→
×
A
C
→
)
×
A
B
→
|
|
A
B
→
|
2
{\displaystyle h_{AB}=|{\overrightarrow {DC}}\,|=\displaystyle {\frac {|({\overrightarrow {AB}}\times {\overrightarrow {AC}})\times {\overrightarrow {AB}}\,|}{|{\overrightarrow {AB}}\,|^{2}}}}
Así que la solución correcta es la (1).