Movimiento plano de disco, barra y cuadrado

Enunciado

El sistema de la figura está formado por un disco de radio $R$ (sólido “0”), que rueda sin deslizar sobre el eje fijo $OX_{1}$, desplazándose su centro $C$ con velocidad constante $v_{0}$, respecto del sistema de referencia fijo $OX_{1}Y_{1}$. Una barra de longitud $8R$ (sólido “2”), tiene un extremo articulado en $C$ y está obligada a pasar por el punto fijo $O$. El otro extremo de la barra ($A$) se encuentra siempre de una acanaladura practicada en el lado de un cuadrado (sólido “3”) que desliza sobre el eje $OX_{1}$.

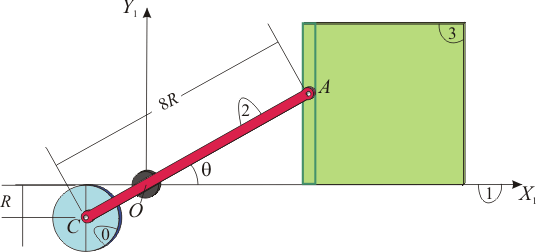
1. Describa las reducciones cinemáticas de los movimientos en función de los datos del enunciado y de la variable geométrica $\theta$.
2. Para una posición arbitraria del sistema, dada por el ángulo $\theta$, determine gráfica o analíticamente -y de manera razonada-, las posiciones de los C.I.R. de todos los movimientos relativos en el sistema.
3. Obtenga las posiciones en las que el cuadrado se detiene (respecto del sólido fijo) y calcule el valor de la aceleración absoluta del cuadrado ($\mathbf {a} _{31}^{A}$) en dicha posición.
4. Calcule las componentes intrínsecas de la velocidad y la aceleración absolutas del extremo $A$ de la barra cuando el sistema se halla en la posición dada por $\theta =\pi /2$.

Solución

Reducciones cinemáticas de todos los movimientos

El sistema mecánico bajo estudio consiste en cuatro sólidos rígidos (considerando como sólido “1” el sistema de referencia fijo $OX_{1}Y_{1}Z_{1}$) en movimiento relativo. El disco, la barra y el cuadrado (sólidos “0”, “2” y “3”, respectivamente), se mueven siempre contenidos en el plano fijo $OX_{1}Y_{1}$, por lo que éste va a ser el plano director de los movimientos planos absolutos $\{i1\}$ (con $i=0,2,3$), cuya dirección normal está definida por el vector unitario cartesiano $\mathbf {k} _{1}$. Pero además, los movimientos relativos $\{20\}$, $\{23\}$ y $\{30\}$, son también movimientos planos cuyos correspondientes planos directores están contenidos en el plano $OX_{1}Y_{1}$. De esta forma, las velocidades instantáneas de cualquier punto, en cualquiera de los movimientos posibles, van a ser siempre perpendiculares a la dirección del eje $OZ_{1}$; en consecuencia, todos los vectores rotación instantánea son paralelos a dicha dirección. Por tanto, se tendrá que,

$\qquad \mathbf {v} _{ij}^{P}(t)\ \perp \ \mathbf {k} _{1}\;\;\Longleftrightarrow \;\;{\vec {\omega }}_{ij}\ \|\ \mathbf {k} _{1}\mathrm {,} \qquad \forall \,P\mathrm {;} \quad \forall \,i,j=0,1,2,3$

Aunque no es estrictamente necesario, puede resultar útil definir sistemas de referencia ligados a cada uno de los sólidos del sistema. En el caso que nos ocupa, y con el fin de simplificar al máximo el análisis, tomaremos los ejes $Z$ de todos ellos perpendiculares al plano $OX_{1}Y_{1}$; es decir, paralelos a la dirección normal común a todos los planos directores:

$\mathbf {k} _{1}=\mathbf {k} _{0}=\mathbf {k} _{2}=\mathbf {k} _{3}=\mathbf {n} \;\;\Longrightarrow \;\;{\vec {\omega }}_{ij}=\omega _{ij}\mathbf {k} _{j}=\omega _{ij}\mathbf {n} \mathrm {,} \quad \forall \ \{ij\}$

Movimiento $\{01\}$

Consideremos el movimiento del disco “0” respecto del sólido fijo “1”. Asociaremos aquél con un sistema de referencia tal que el propio disco define el plano $CX_{0}Y_{0}$. De los datos indicados en el enunciado se desprende que el centro $C$ del disco realiza un movimiento rectilíneo uniforme de velocidad conocida $v_{0}$ y trayectoria paralela al eje $OX_{1}$. Concretamente, las ecuaciones de movimiento de este punto, expresada los ejes del sólido “1” son:

${\overrightarrow {OC}}=\mathbf {r} _{C}\rfloor _{{}_{1}}(t)=x_{C}(t)\mathbf {i} _{1}-R\mathbf {j} _{1}\mathrm {;} \quad \mathrm {tal\;\;que,} \quad \;{\frac {\mathrm {d} \mathbf {r} _{C}}{\mathrm {d} t}}{\bigg \rfloor }_{1}={\dot {x}}_{C}(t)\mathbf {i} _{1}=v_{0}\mathbf {i} _{1}=\mathbf {v} _{01}^{C}(t)\mathrm {,} \;\;\mathrm {cte.}$

Y como rueda sin deslizar sobre el eje $OX_{1}$, el punto $I$ del disco que, en un determinado instante, se encuentra en contacto con dicho eje tiene velocidad nula. Teniendo en cuenta que en dicho instante ${\overrightarrow {CI}}=R\mathbf {j} _{1}$, y aplicando el teorema de Chasles, obtenemos:

$\mathbf {0} =\mathbf {v} _{01}^{I}=\mathbf {v} _{01}^{C}+{\vec {\omega }}_{01}\times {\overrightarrow {CI}}=\left(v_{0}-R\omega _{01}\right)\mathbf {i} _{1}\;\;\Longrightarrow \;\;\omega _{01}={\frac {v_{0}}{R}}$

Obsérvese que, al realizar $C$ un movimiento rectilíneo uniforme, el resultado anterior es independiente del instante considerado. Por tanto, obtendremos la reducción cinemática del movimiento $\{01\}$ para cualquier instante de tiempo:

$\forall \,t\mathrm {,} \;\;\;\{01\}\equiv {\begin{cases}\displaystyle {\vec {\omega }}_{01}(t)={\frac {v_{0}}{R}}\mathbf {k} _{1}&{}\\\\\displaystyle \mathbf {v} _{01}^{C}(t)=v_{0}\mathbf {i} _{1}&{}\end{cases}}\;$

 

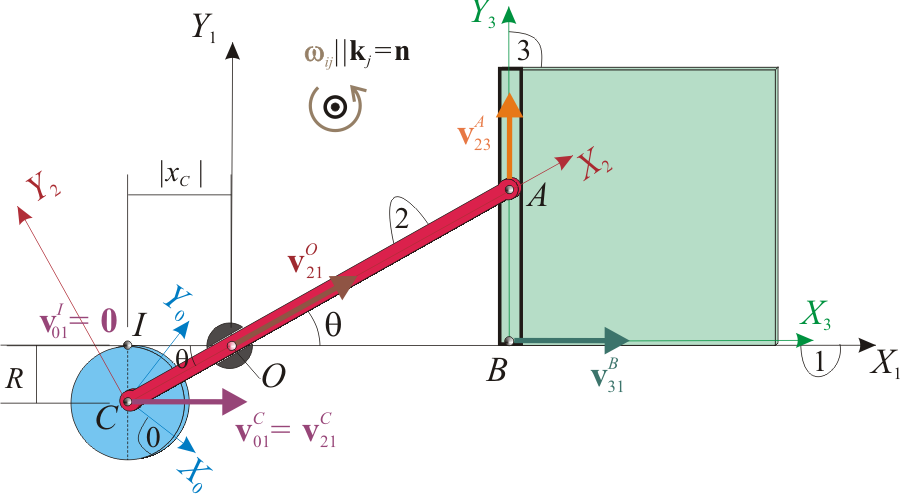
Movimiento $\{21\}$

Como sistema de referencia asociado al sólido “2” tomaremos el $CX_{2}Y_{2}Z_{2}$ de manera que $CX_{2}$ sea colineal con la barra $CA$. Así, se tendrá que $\theta (t)$ es el ángulo que van a formar los ejes $CX_{2}$ y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} en el transcurso del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{21\}} . Aplicando las fórmulas de Poisson se obtiene...

$\left.{\begin{array}{l}\mathbf {i} _{2}(t)=\mathrm {cos} \!\ \theta (t)\mathbf {i} _{1}+\mathrm {sen} \!\ \theta (t)\mathbf {j} _{1}\\\\\mathbf {j} _{2}(t)=-\mathrm {sen} \!\ \theta (t)\mathbf {i} _{1}+\mathrm {cos} \!\ \theta (t)\mathbf {j} _{1}\end{array}}\right\}\;\Longrightarrow \;{\frac {\mathrm {d} \mathbf {i} _{2}}{\mathrm {d} t}}{\bigg \rfloor }_{1}={\dot {\theta }}(t)\ \mathbf {j} _{2}(t)={\vec {\omega }}_{21}\times \mathbf {i} _{2}\;\;\Longrightarrow \;\;{\vec {\omega }}_{21}(t)={\dot {\theta }}(t)\mathbf {k} _{1}$

Además, el extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} de la barra coincide en todo momento con el centro del disco, de manera que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \quad\mathbf{v}_{21}^C(t)=\mathbf{v}_{01}^C(t)=v_0\mathbf{i}_1} .

Luego, para obtener la reducción cinemática del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{21\}} hemos de determinar la ley Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}(t)} . Esto podemos hacerlo por diferentes procedimientos. Por ejemplo, a partir de la geometría del sistema: como el pasador que hay situado en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} del sólido fijo obliga a que la barra pase siempre por allí, la coordenada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_C} del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} deberá ser tal que en cada instante se verifque...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tan}\!\ \theta (t)=\frac{|\overrightarrow{CI}|}{|\overrightarrow{OI}|}=-\frac{R}{x_C(t)}\quad\longrightarrow\quad\dot{x}_C(t)=\frac{R\ \dot{\theta}(t)}{\mathrm{sen}^2\theta(t)}=v_0\quad\Longrightarrow\quad\dot{\theta}(t)=\frac{v_0}{R}\ \mathrm{sen}^2\theta(t)}

Este mismo resultado lo podemos obtener por mediante un procedimeinto puramente cinemático: además de conocer la velocidad del extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} de la barra, el pasador en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} obligará a la barra a moverse de manera que el punto de ésta que coincide con dicho punto geométrico tiene velocidad colineal con la barra; además, debe verficiarse el teorema de Chasles, de manera que,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{21}^O (t)=v(t)\mathbf{i}_2(t)=\mathbf{v}_{21}^C+\vec{\omega}_{21}\times\overrightarrow{CO}\mathrm{;}\quad\;\mathrm{siendo}\quad\overrightarrow{CO}=\frac{R}{\mathrm{sen}\!\ \theta}\ \mathbf{i}_2}

Proyectando sobre el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle CY_2} se tendrá:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=\mathbf{j}_2\cdot\mathbf{v}_{21}^O=\mathbf{j}_2\cdot\mathbf{v}_{21}^C+\mathbf{j}_2\cdot\left(\vec{\omega}_{21}\times\overrightarrow{CO}\right)\quad\longrightarrow\quad 0=-v_0\mathrm{sen}\!\ \theta\ +\ \frac{R\ \dot{\theta}(t)}{\mathrm{sen}\!\ \theta}\quad\Longrightarrow\quad\dot{\theta}(t)=\frac{v_0}{R}\ \mathrm{sen}^2\theta(t)}

Por tanto, la reducción cinemática instantánea del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{21\}} en el instante en que la barra y el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} forman un ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta} , es:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \forall\ t\mathrm{,} \;\; \{21\}\equiv\begin{cases}\displaystyle\vec{\omega}_{21}(t)=\frac{v_0}{R}\ \mathrm{sen}^2\theta (t)\mathbf{k}_1&{}\\ \\ \displaystyle\mathbf{v}_{21}^C(t)=v_0\mathbf{i}_1&{}\end{cases}\;}

Movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{31\}}

En el enunciado se indica que el sólido “3” (cuadrado) se mueve de manera que uno de sus lados desliza en todo momento sobre el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} . Definamos los ejes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle BX_3Y_3Z_3} de manera que las direcciones Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle BX_3} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle BY_3} sean parelelas a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OY_1} en todo instante, se tendrán entonces:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \big\{\mathbf{i}_3(t)=\mathbf{i}_1\mathrm{;}\;\ \mathbf{j}_3(t)=\mathbf{j}_1\mathrm{;}\;\ \mathbf{k}_3(t)=\mathbf{k}_1\big\}\quad\Longleftrightarrow\quad\vec{\omega}_{31}(t)=\mathbf{0}\mathrm{,}\;\;\;\forall\ t}

Es decir, el movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{31\}} es una traslación permanente. Para caracterizarlo necesitamos, por tanto, conocer la velocidad de cualquier punto del cuadrado medida respecto del sistema de referencia fijo. Consideremos, por ejemplo, el vértice Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} cuya posición en cada instante viene dada por la proyección del extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} de la barra. Es fácil, por tanto, determinar las ecuaciones horarias que describen la posición del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E} en su movimiento respecto del sólido “1”, en función del parámetro geométrico variable Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta (t)} :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left.\begin{array}{r}\overrightarrow{OB}=\mathbf{r}_B(t)\mathrm{;}\;\, \overrightarrow{OA}=\mathbf{r}_A(t)\;\,\Rightarrow\;\mathbf{r}_B(t)=\big[\mathbf{i}_1\cdot\mathbf{r}_A(t)\big]\cdot\mathbf{i}_1= |\overrightarrow{OA}|\mathrm{cos}\!\ \theta(t)\ \mathbf{i}_1 \\ \\ \displaystyle |\overrightarrow{OA}|=8R-|\overrightarrow{CO}|=R\left(8-\frac{1}{\mathrm{sen}\!\ \theta}\right)\end{array}\right\}\quad\Longrightarrow\quad \mathbf{r}_B(t)=R\big[8\ \mathrm{cos}\!\ \theta(t)-\mathrm{cot}\!\ \theta(t)\big]\ \mathbf{i}_1}

La derivada temporal de esta ecuación horaria, medida respecto del sistema de referencia fijo “1” es la velocidad instantánea del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} y, por consiguiente, la velocidad de cualquier otro punto del cuadrado “3” en su movimiento de traslación respecto del sólido “1”:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathrm{d}\mathbf{r}_B}{\mathrm{d}t}\bigg\rfloor_1=R\ \dot{\theta} (t)\ \left[-8\ \mathrm{sen}\!\ \theta(t)+\frac{1}{\mathrm{sen}^2 \theta(t)}\right]\ \mathbf{i}_1=\mathbf{v}_{31}^B(t) \mathrm{,}}

... y sustituyendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}(t)} ...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \forall\, t\mathrm{,} \;\;\; \{31\}\equiv\begin{cases}\displaystyle\vec{\omega}_{31}(t)=\mathbf{0}&{}\\ \\ \displaystyle\mathbf{v}_{31}^B(t)=v_0\big[1-8\mathrm{sen}^3\theta(t)\big]\ \mathbf{i}_1=\mathbf{v}_{31}^P(t)\mathrm{,}\quad\forall\, P&{}\end{cases}\;}

También podríamos haber obtenido la velocidad de traslación del cuadrado mediante un procedimiento puramente cinemático. De la composición de velocidades tendríamos que, en cada instante, se ha de verificar...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{21}^A=\mathbf{v}_{23}^A+\mathbf{v}_{31}^A}

El extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} de la barra “2” siempre desliza sobre el lado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle BD} del cuadrado “3”, mientras que éste se traslada pararelo al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} ; se tendrá, por tanto:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left.\begin{array}{c}\mathbf{v}_{23}^A(t)\ \| \ \mathbf{j}_{3}=\mathbf{j}_{1} \perp \mathbf{i}_1\\ \\ \mathbf{v}_{31}^A(t)\ \| \ \mathbf{i}_{3}=\mathbf{i}_1\end{array}\right\}\quad\Longrightarrow\quad\mathbf{v}_{31}^A(t)=\big[\mathbf{i}_1\cdot\mathbf{v}_{21}^A(t)\big]\cdot\mathbf{i}_1=\mathbf{v}_{31}^P(t)\mathrm{,}\quad\forall\, P\mathrm{,}\quad\forall\, t}

Es decir, la velocidad de traslación del cuadrado “3” en su movimiento absoluto respecto del sistema de referencia fijo, coincide con la componente horizontal (en la dirección Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} ) de la velocidad del extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} de la barra “2”. Así que, calculando Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{21}^A (t)} a partir de la reducción cinemática del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{21\}} y aplicando la expresión anterior, se obtiene el valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{31}^P (t)} , para cualquier punto del cuadrado.

 

Una vez obtenidas las reducciones cinemáticas instantáneas de los movimientos que podemos denominar absolutos por estar referidos al sólido fijo “1”, aplicaremos las leyes de composición de movimientos relativos para obtener las del resto de movimientos. Recuérdese que estas leyes de composición tienen un carácter instantáneo. Sin embargo, como en las reducciones que hemos calculado las magnitudes cinemáticas están expresadas como funciones del tiempo, las reducciones que obtengamos por composición describirán los movimientos relativos en cualquier instante.

 

Movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{20\}}

Utilizando las reducciones cinemáticas de los movimientos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{01\}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{21\}} ,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left.\begin{array}{c}\vec{\omega}_{20}(t)=\vec{\omega}_{21}(t)+\vec{\omega}_{10}(t)=\vec{\omega}_{21}(t)-\vec{\omega}_{01}(t)\\ \\ \mathbf{v}_{20}^C(t)=\mathbf{v}_{21}^C(t)+\mathbf{v}_{10}^C(t)=\mathbf{v}_{21}^C(t)-\mathbf{v}_{01}^C(t)\end{array}\right\}}  ⇒  Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \forall\ t\mathrm{,} \;\; \{20\}\equiv\begin{cases}\displaystyle\vec{\omega}_{20}(t)=\frac{v_0}{R}\big[ \mathrm{sen}^2\theta (t)-1\big]\mathbf{k}_1=-\frac{v_0}{R}\ \mathrm{cos}^2\theta (t)\ \mathbf{k}_0&{}\\ \\ \displaystyle\mathbf{v}_{20}^C(t)=\mathbf{0}&{}\end{cases}\;}

Es decir, la barra “2” realiza un movimiento permanente de rotación respecto del disco “0”, girando en el plano director alrededor del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} , que es extremo de la barra y centro del disco.

Movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{03\}}

Haciendo lo propio con las reducciones cinemáticas de los movimientos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{01\}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{31\}} ...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left.\begin{array}{c}\vec{\omega}_{03}(t)=\vec{\omega}_{01}(t)+\vec{\omega}_{13}(t)=\vec{\omega}_{01}(t)-\overbrace{\vec{\omega}_{31}(t)}^{=\mathbf{0}}=\vec{\omega}_{01}(t)\\ \\ \mathbf{v}_{03}^C(t)=\mathbf{v}_{01}^C(t)+\mathbf{v}_{13}^C(t)=\mathbf{v}_{01}^C(t)-\mathbf{v}_{31}^P(t)\end{array}\right\}}  ⇒  Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \forall\ t\mathrm{,} \;\; \{03\}\equiv\begin{cases}\displaystyle\vec{\omega}_{03}(t)=\frac{v_0}{R}\ \mathbf{k}_1&{}\\ \\ \displaystyle\mathbf{v}_{03}^C(t)=8v_0\!\ \mathrm{sen}^3\theta(t)\ \mathbf{i}_3&{}\end{cases}\;}

Movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{23\}}

Y para describir el movimiento relativo de la barra respecto del cuadrado, utilizaremos las reducciones de los movimientos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{21\}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{31\}} . La reducción del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{23\}} puede realizarse en cualquier punto; sin embargo, optaremos por reducir en el extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} , ya que es el punto material de la barra que realiza un movimiento más simple: en todo instante se desplaza por el lado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle BD} del cuadrado:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{c}\vec{\omega}_{23}(t)=\vec{\omega}_{21}(t)+\vec{\omega}_{13}(t)=\vec{\omega}_{21}(t)-\overbrace{\vec{\omega}_{31}(t)}^{=\mathbf{0}}=\vec{\omega}_{21}(t)\\ \\ \mathbf{v}_{23}^A(t)=\mathbf{v}_{21}^A(t)+\mathbf{v}_{13}^A(t)=\mathbf{v}_{21}^A(t)-\mathbf{v}_{31}^P(t)\end{array}}

Calculemos la velocidad del extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} en su movimiento absoluto a partir de la reducción del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{21\}} y teniendo en cuenta que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \;\overrightarrow{CA}=8R\ \mathbf{i}_2(t)} :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{21}^A(t)=\mathbf{v}_{21}^C+\vec{\omega}_{21}\times\overrightarrow{CA}=v_0\ \mathbf{i}_1+8R\ \dot{\theta}(t)\mathbf{j}_2(t)=v_0\ \big[1-8\mathrm{sen}^3\theta(t)\big]\mathbf{i}_1+v_0\ \mathrm{sen}^2\theta(t)\!\ \mathrm{cos}\!\ \theta(t)\mathbf{j}_1 }

Por tanto, la reducción cinemática que describe el movimiento de la barra respecto del cuadrado es...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \forall\ t\mathrm{,} \;\; \{23\}\equiv\begin{cases}\displaystyle\vec{\omega}_{23}(t)=\frac{v_0}{R}\ \mathrm{sen}^2\theta(t)\ \mathbf{k}_1&{}\\ \\ \displaystyle\mathbf{v}_{23}^A(t)=v_0\!\ \mathrm{sen}^2\theta(t)\!\ \mathrm{cos}\!\ \theta(t)\mathbf{j}_3&{}\end{cases}\;}

Centros instantáneos de rotación

Conocida la reducción cinemática instantánea de un movimiento plano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{ij\}} , la posición de su correspondiente centro intantáneo de rotación Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{ij}} respecto del punto de reducción queda determinada en cada instante por la expresión analítica...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{ij\}\equiv\bigg\{\vec{\omega}_{ij}\mathrm{;}\;\;\;\mathbf{v}_{ij}^P\bigg\}}  ⇒  Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{PI}_{ij}=\frac{\vec{\omega}_{ij}\times\mathbf{v}_{ij}^P}{|\vec{\omega}_{ij}|^2}}

En el apartado anterior hemos obtenido las magnitudes cinemáticas que describen cada uno de los distintos movimientos (absolutos y relativos) que se distinguen en el sistema, expresándolas en términos de los datos conocidos y de la variable geométrica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta} . Por tanto, podemos determinar analíticamente las posiciones de cualquiera de los C.I.R. en cualquier instante o, lo que es lo mismo, para cualquier configuración geométrica del sistema mecánico bajo estudio. Por otra parte, como todos los movimientos se producen en planos directores superpuestos al Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1Y_1} , los C.I.R. de todos ellos se encuentran contenidos en dicho plano.

 

Pero veamos cómo se determinarían las posiciones de los C.I.R. mediante métodos gráficos; es decir, utilizando las propiedades geométricas de los campos de velocidades correspondientes a los diferentes movimientos planos. Como se sabe, con estos procedimientos no es necesario conocer de forma explícita las reducciones cinemáticas. De hecho, éstas pueden calcularse después de que los centros instantáneos de rotación han sido obtenidos gráficamente.

Hay dos movimientos en el sistema cuyos C.I.R. están determinados de manera inmediata. Se trata del Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{20}} y del Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{01}} . El extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} de la barra “2” coincide en todo momento con el centro del disco Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0} por tanto dicho punto se halla en reposo permantente en el movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{20\}} . Por tanto, dicho punto es el centro permanente de rotación de dicho movimiento. Por otra parte, el disco “0” rueda sin deslizar sobre el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} , por lo que el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I} del sólido “0” que se halla en contacto con dicho eje será el C.I.R. del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{01\}} en dicho instante:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \forall\, t\mathrm{,}\;\;I_{20}=C\;\longleftrightarrow\;\overrightarrow{CI}_{20}=\mathbf{0}}     Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{01}=I\mathrm{,}\;\;\; \mathrm{tal}\;\, \mathrm{que}\;\;\;\overrightarrow{CI}_{01}=R\mathbf{j}_1}

Aplicando el Teorema de los tres centros, tendremos que la recta Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_{201}} que en un determinado instante contiene a los C.I.R. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{20}} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{01}} e Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{21}} pasa por los puntos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} e Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I} , por lo que su dirección viene dada por el unitario Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{j}_1} . Se tendrá, por tanto...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{20}\mathrm{,}\;I_{01}\mathrm{,}\;I_{21} \in\Delta_{201}\|\mathbf{j}_1\quad\Longrightarrow\quad\overrightarrow{CI}_{21}=\lambda\ \mathbf{j}_1}

siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \lambda} la distancia que separa dicho C.I.R. del centro del disco en un determinado instante. En general, el valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \lambda} dependerá de la posición del sistema, lo cuál es equivalente a decir que será función del parámetro Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta} . Para obtener Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \lambda} necesitamos otra propiedad geométrica del campo de velocidades: por ejemplo que, al estar la barra obligada a pasar por el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} , la velocidad del punto material del sólido “2” que coincide con dicho punto geométrico debe ser colineal con la barra. Consecuentemente, el C.I.R. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{21}} debe estar en la recta Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_O} que pasa por el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} y es perpendicular a la barra; es decir, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{21}} debe estar a una cierta distancia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mu} (que también dependerá del valor del Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta} ), en la dirección marcada por el unitario Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{j}_2} :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{i}_2\ \|\ \mathbf{v}_{21}^O=\overrightarrow{OI}_{21}\times\vec{\omega}_{21}\quad\Longrightarrow\quad\begin{cases}O\mathrm{,}\;I_{21} \in\Delta_{O}\ \|\ \mathbf{j}_2&{}\\ \\ \mathbf{i}_2\perp\overrightarrow{OI}_{21}=\mu\ \mathbf{j}_2&{} \end{cases}}

Como el C.I.R. de un movimiento plano es un punto único en cada instante, podemos obtener la posición de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{21}} exigiendo que se verifique la relación vectorial,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OI}_{21}=\overrightarrow{OC}+\overrightarrow{CI}_{21}}

Ésta proporcionará sendas ecuaciones albegraicas (una por cada componente cartesiana) expresadas en términos de los datos del problema y de la variable Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta} , y cuyas incógnitas serán las distancias Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \lambda} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mu} que separan a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{21}} de los puntos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} , respectivamente.

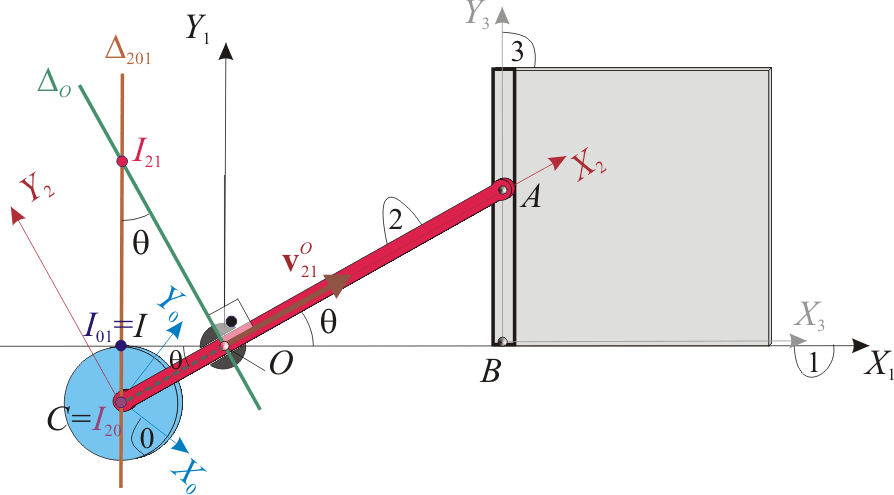
Pero también podemos optar por la resolución puramente geométrica: según los resultados anterior, el C.I.R. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{21}} debe ser el punto de interscción de las rectas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_{201}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_O} , de manera que los puntos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle COI_{21}} son los vértices de un triángulo, rectángulo en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} ; además, el ángulo en el vértice Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{21}} es el que forman las direcciones Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{j}_2} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{j}_1} , es decir, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta} . Por tanto, se deberá cumplir:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_{201}\bigcap\Delta_O=I_{21}}    ⇒   Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\!\ \theta=\frac{|\overrightarrow{CO}|}{|\overrightarrow{CI}_{21}|}=\frac{R/\mathrm{sen}\!\ \theta}{\lambda}}    ⇒   Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{CI}_{21}=\lambda(\theta)\ \mathbf{j}_1=\frac{R}{\mathrm{sen}^2\theta}\ \mathbf{j}_1}

Como vimos en el apartado anterior, el movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{31\}} es una traslación permanente paralela al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} . Por tanto, el C.I.R. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{31}} están en el infinito, en cualquier recta contenida en el plano director y perpendicular a las velocidades Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{31}^P} ; es decir, en toda recta cuya dirección viene dada por el unitario Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{j}_1} . Si aplicamos de nuevo el teorema de los tres centros, tendremos que los centros instantáneos de rotación Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{21}} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{31}} (en el infinito) e Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{23}} estarán alineados en la recta Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_{231}} que debe pasar por el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{21}} y se extiende hasta el infinito en la dirección paralela al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OY_1} . Obsérvese que una recta con estas propiedades coincide con la Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_{201}} :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{21}\mathrm{,}\;I_{31}\mathrm{,}\;I_{23} \in\Delta_{231}\ \|\ \mathbf{j}_1\quad\Longrightarrow\quad\Delta_{231}=\Delta_{201}\quad\Longrightarrow\quad \overrightarrow{CI}_{23}=\nu(\theta)\ \mathbf{j}_1}

 

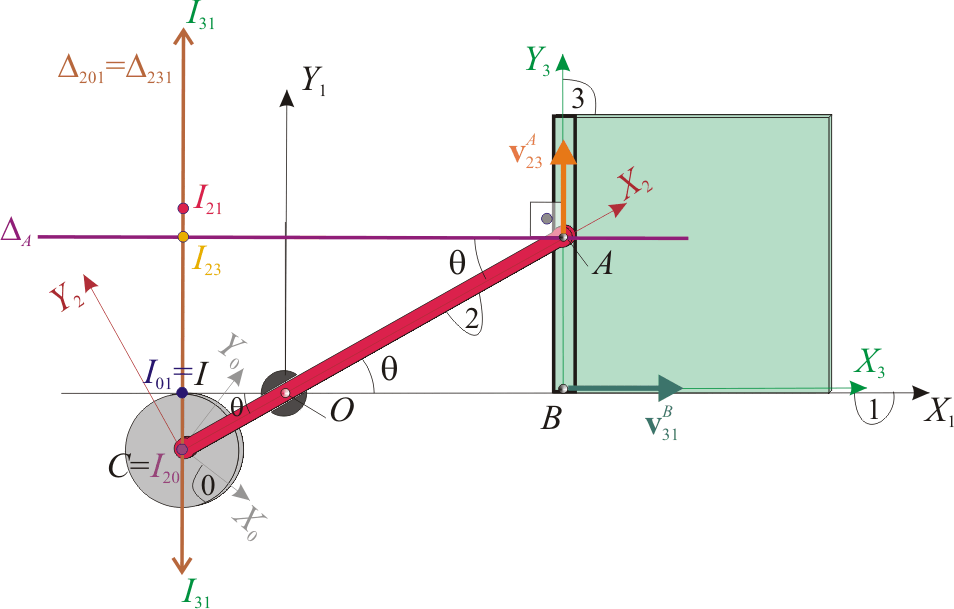
Para determinar la distancia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \nu(\theta)} debemos utilizar una nueva propiedad del campo de velocidades del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{23\}} : el C.I.R. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{23}} debe encontrarse sobre la recta Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_A} que pasa por el extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} y tiene dirección perpendicular a la velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{23}^A} del movimiento relativo de la barra “2” respecto del cuadrado “3”. La posición de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{23}} se corresponde con el punto de intersección de estas dos rectas:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left.\begin{array}{l}I_{23}\ \in\Delta_{231}\ \|\ \mathbf{j}_1\\ \\ I_{23}\ \in\Delta_A\ \|\ \mathbf{i}_1\end{array}\right\}\quad\Longrightarrow\quad\Delta_{231}\bigcap\Delta_A=I_{23}\quad\Longrightarrow\quad\mathrm{sen}\!\ \theta=\frac{|\overrightarrow{CI}_{23}|}{|\overrightarrow{CA}|}=\frac{\nu}{8R}}    ⇒   Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{CI}_{23}=\nu(\theta)\ \mathbf{j}_1=8R\ \mathrm{sen}\!\ \theta\ \mathbf{j}_1}

Aún queda por determinar el C.I.R. del movimiento relativo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{03\}} . Aplicando de nuevo el teorema de los tres centros tenemos que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{03}} debe estar alineado con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{01}} e Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{31}} ; es decir, debe estar en la recta Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_{031}} que pasa por el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{01}=I} y tiene la dirección del vector unitario cartesiano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{j}_1} . Pero también, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{03}} debe pertenecer a la recta Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_{032}} , definida por los puntos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{20}=C} e Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{23}} No obstante, no podemos determinar el C.I.R. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{23}} como el punto de intersección de estas rectas ya que ¡ambas son el mismo conjunto de puntos! De hecho, puede comprobarse que...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta_{031}=\Delta_{032}=\Delta_{231}=\Delta_{201}}

Tampoco podemos determinarlo a partir de las velocidades de algún punto, pues las que pueden determinarse fácilmente son...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{03}^I=\overbrace{\mathbf{v}_{01}^I}^{=\mathbf{0}}-\mathbf{v}_{31}^I=v_I\ \mathbf{i}_1,}   ... o bien,...   Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{03}^C=\mathbf{v}_{01}^C-\mathbf{v}_{31}^C=v_C\ \mathbf{i}_1}

por lo que el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I_{03}} debe estar en la recta que pasa por Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I} o Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} , y es perpendicular al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} ; es decir, la misma que hemos determinado antes. En consecuencia, la única opción que queda es determinar analíticamente la posición de este C.I.R. a partir de la reducción cinemética correspondiente:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{CI}_{03}=\frac{\vec{\omega}_{03}\times\mathbf{v}_{03}^C}{|\vec{\omega}_{03}|^2}=\frac{R^2}{v_0^2}\ \left(\frac{v_0}{R}\ \mathbf{k}_1\right)\times\big(8v_0\!\ \mathrm{sen}^3 \theta\ \mathbf{i}_1\big)}  ⇒  Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{CI}_{03}=8R\!\ \mathrm{sen}^3 \theta\ \mathbf{j}_1}

 

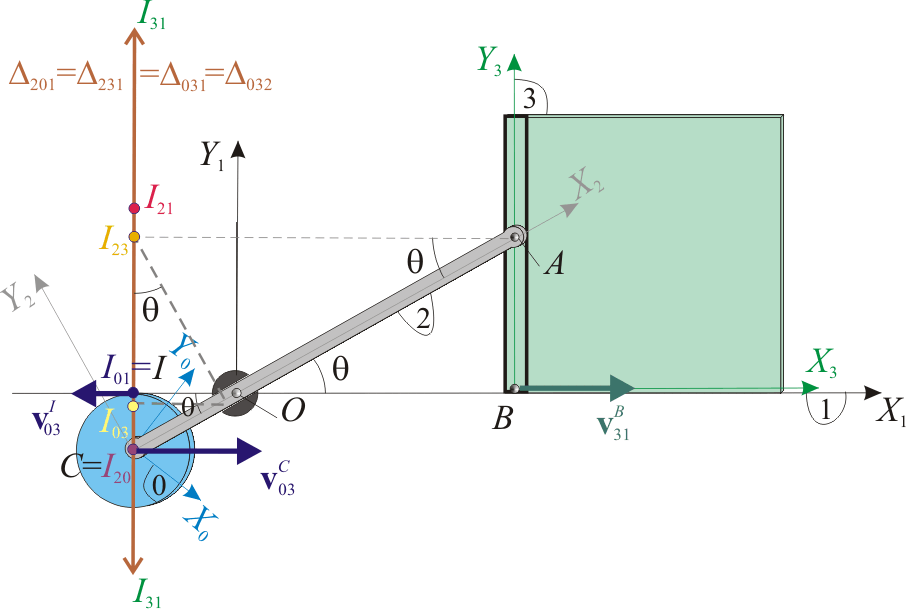
Obsérvese que los seis C.I.R. están alineados en la misma recta que pasa por los puntos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle I} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} y es paralela al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} .

Posiciones de reposo del cuadrado

Las posiciones de reposo del sólido “3” las determinaremos a partir de la reducción cinemática del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{31\}} , cuyas magnitudes cinemáticas están expresadas en términos de la variable geométrica que describe la posición del sistema en cada instante de tiempo, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta (t)} . Como este movimiento absoluto es una traslación permanente (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{31}=\mathbf{0}\mathrm{,}\;\;\forall\, \theta(t)} ), la condicón de reposo instantáneo consiste en exigir que la velocidad absoluta de cualquier punto del cuadrado sea nula:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{31}^P(\theta_0)=v_0\big[1-8\mathrm{sen}^3\theta_0\big]\ \mathbf{i}_1=\mathbf{0}\qquad\Rightarrow\qquad} Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\!\ \theta_0=\frac{1}{2}\;\;\equiv\;\;\ \theta_0=\frac{\pi}{6}\mathrm{;}\;\frac{5\pi}{6}}

Es decir, cuando la barra forma un ángulo de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \pi/6} o de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 5\pi/6} con el eje fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} , el cuadrado “3 ” se encuentra en reposo. Para comprobar que se trata de un reposo instantáno calcularemos la aceleración de cualquier punto del cuadrado en el instante en que el parámetro Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta} presenta esos valores. Y puesto que tenemos la expresión de la velocidad absoluta del cuadrado como una función de la ley horaria Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta (t)} , derivaremos con respecto al tiempo para obtener la expresión de dicha aceleración en cualquier instante de tiempo:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{a}_{31}^P(t)=\frac{\mathrm{d}\mathbf{v}_{31}^P}{\mathrm{d}t}\bigg\rfloor_1=\dot{\theta} (t)\ \frac{\mathrm{d}\mathbf{v}_{31}^P}{\mathrm{d}\theta}\bigg\rfloor_1=-24v_0\ \dot{\theta} (t)\!\ \mathrm{sen}^2 \theta(t)\!\ \mathrm{cos}\!\ \theta(t)\ \mathbf{i}_1\mathrm{;}\;\;\;\forall\, P}

Sustituyendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}(t)} en la anterior expresión, se obtiene...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{a}_{31}^P(\theta)=-24\ \frac{v_0^2}{R}\ \mathrm{sen}^4 \theta\!\ \mathrm{cos}\!\ \theta\ \mathbf{i}_1\qquad\Rightarrow\qquad} Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{a}_{31}^P\left(\frac{\pi}{6}\right)=-\frac{3 \sqrt{3}}{4}\ \frac{v_0^2}{R}\ \mathbf{i}_1=-\mathbf{a}_{31}^P\left(\frac{5\pi}{6}\right) }

Aceleración del extremo A de la barra

Consideremos ahora el movimiento absoluto de la barra “2” respecto del sólido fijo “1”. En el primer apartado se realizó la reducción cinemática del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{21\}} en el extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} , luego para obtener la aceleración del otro extremo aplicamos la expresión general del campo de aceleraciones para el movimiento plano de una sólido rígido:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{a}_{21}^A(t)=\mathbf{a}_{21}^C+\vec{\alpha}_{21}\times\overrightarrow{CA}+\vec{\omega}_{21}\times\big(\vec{\omega}_{21}\times\overrightarrow{CA}\big)=\mathbf{a}_{21}^C(t)+\vec{\alpha}_{21}(t)\times\overrightarrow{CA}-|\vec{\omega}_{21}(t)|^2\!\ \overrightarrow{CA}}

Para obtener los términos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{a}_{21}^C(t)} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\alpha}_{21}(t)} derivamos con respecto al tiempo las leyes horarias de las magnitudes cinemáticas expresadas en la reducción cinemática del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{21\}} . Como el extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle C} realiza un movimiento rectilíneo uniforme paralelo al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_1} , su aceleración es nula; por el contrario, el vector rotación de este movimiento depende de la posición de la barra y, por consiguiente del tiempo:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{a}_{21}^C(t)=\frac{\mathrm{d}\mathbf{v}_{21}^C}{\mathrm{d}t}\bigg\rfloor_1=\mathbf{0}\mathrm{,} \;\;\forall\, \theta(t) \mathrm{;}\qquad\qquad\vec{\alpha}_{21}(t)=\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\bigg\rfloor_1=\dot{\theta} (t)\ \frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}\theta}\bigg\rfloor_1=-\frac{2v_0^2}{R^2}\ \mathrm{sen}^3 \theta(t)\!\ \mathrm{cos}\!\ \theta(t)\ \mathbf{k}_1=\vec{\alpha}_{21}[\theta(t)]}

Utilizando además la reducción del movimiento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{21\}} , obtenemos los valores de las magntides geométricas y cinemáticas en la posición dada por Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta=\pi/2} los valores de las magnitudes cinemáticas del movimiento de la barra son:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{a}_{21}^C\left(\frac{\pi}{2}\right)=\mathbf{0}\mathrm{;}\qquad\vec{\alpha}_{21}\left(\frac{\pi}{2}\right)=\mathbf{0}\mathrm{;}\qquad\vec{\omega}_{21}\left(\frac{\pi}{2}\right)=\frac{v_0}{R}\ \mathbf{k}_1\mathrm{;}\qquad\overrightarrow{CA}\rfloor_{{}_{\pi/2}}=8R\ \mathbf{j}_1}   

Sustituyendo en la expresión de la aceleración del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} , se obtiene...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{a}_{21}^A\left(\frac{\pi}{2}\right)=\underbrace{\mathbf{a}_{21}^C}_{=\mathbf{0}}+\underbrace{\vec{\alpha}_{21}\times\overrightarrow{CA}}_{=\mathbf{0}}-\left[|\vec{\omega}_{21}(t)|^2\!\ \overrightarrow{CA}\right]_{\pi/2}=-\frac{8v_0^2}{R}\ \mathbf{j}_1}

Pero en el enunciado nos preguntan por las componentes intrísecas de esta aceleración. Es decir, por las proyecciones de dicha magnitud vectorial, en el instante considerado, sobre las direcciones tangencial y normal a la trayectoria seguida por dicho punto:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{a}_{21}^A\left(\frac{\pi}{2}\right)=a_T\mathbf{T}\rfloor_{{}_{\pi/2}}+a_N\mathbf{N}\rfloor_{{}_{\pi/2}}}

Luego, sólo queda determinar cuáles son los vectores tangente y normal a la trayectoria en el instante en que la barra se halla alineada con el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OY_1} (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta0\pi/2} ), y para ello nos fijamos en la velocidad absoluta del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} en dicho instante. Según calculamos en el primer apartado...

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{v}_{21}^A(\theta)=v_0\ \big(1-8\mathrm{sen}^3\theta\big)\mathbf{i}_1+v_0\ \mathrm{sen}^2\theta\!\ \mathrm{cos}\!\ \theta\mathbf{j}_1\quad\Longrightarrow\quad\mathbf{v}_{21}^A\left(\frac{\pi}{2}\right)=-7v_0\ \mathbf{i}_1}  ⇒ Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{T}\rfloor_{{}_{\pi/2}}=-\mathbf{i}_1}

Si comparamos con el valor obtenido para la aceleración de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} , comprobamos que ésta no tiene componente tangencial en la posición indicada, por lo que toda ella deberá ser aceleración normal. Por otra parte, como la componente Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a_N} no puede ser negativa, deducimos que el vector normal a la trayectoria de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta=\pi/2} coincide con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -\mathbf{j}_1} :

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{a}_T^A\left(\frac{\pi}{2}\right)=a_T\mathbf{T}\rfloor_{{}_{\pi/2}}=\mathbf{0}\mathrm{;}\qquad\;\mathbf{a}_N^A\left(\frac{\pi}{2}\right)=a_N\mathbf{T}\rfloor_{{}_{\pi/2}}=-\frac{8v_0^2}{R}\ \mathbf{j}_1}  ⇒ Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbf{N}\rfloor_{{}_{\pi/2}}=-\mathbf{j}_1}