Movimiento con aceleración constante (GIOI)

Enunciado

Una partícula se mueve con aceleración constante ${\vec {a}}_{0}=-4{\vec {\imath }}$ (m/s²), siendo su posición inicial el origen de coordenadas y su velocidad inicial ${\vec {v}}_{0}=16{\vec {\imath }}+12{\vec {\jmath }}$ (m/s).

1. Halle su posición como función del tiempo.
2. Determine el instante en que la rapidez o celeridad es mínima. Para este instante halle:
   1. La aceleración tangencial y la normal (escalares)
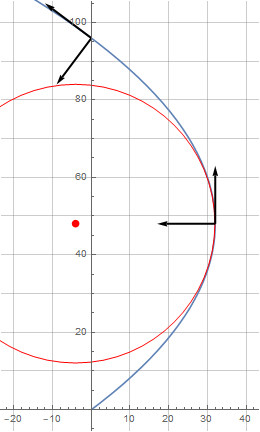
   2. Los vectores del triedro de Frenet
   3. El radio de curvatura
   4. El centro de curvatura
3. Calcule en qué instante vuelve a pasar por el eje OY. Para este instante halle:
   1. La posición y la velocidad
   2. Los vectores del triedro de Frenet
   3. La aceleración tangencial y la normal (escalares)

Resultados

Todo en las unidades fundamentales del SI.

Posición

Posición

${\vec {r}}={\vec {r}}_{0}+{\vec {v}}_{0}t+{\frac {1}{2}}{\vec {a}}_{0}t^{2}=(16t-2t^{2}){\vec {\imath }}+12t{\vec {\jmath }}$

Velocidad

${\vec {v}}={\vec {v}}_{0}+{\vec {a}}_{0}t=(16-4t){\vec {\imath }}+12{\vec {\jmath }}$

Aceleración

${\vec {a}}={\vec {a}}_{0}=-4{\vec {\imath }}$

Instante de rapidez mínima

Valor de t

$a_{t}=0\qquad \Rightarrow \qquad {\vec {a}}\cdot {\vec {v}}=0\qquad \Rightarrow \qquad t=4$

Posición, velocidad y aceleración en t=4

${\vec {r}}=32{\vec {\imath }}+48{\vec {\jmath }}\qquad \qquad {\vec {v}}=12{\vec {\jmath }}\qquad \qquad {\vec {a}}=-4{\vec {\imath }}$

Componentes intrínsecas de la aceleración

$a_{t}=0\qquad \Rightarrow \qquad {\vec {a}}_{n}={\vec {a}}=-4{\vec {\imath }}\qquad \Rightarrow \qquad a_{n}=|{\vec {a}}_{n}|=4$

Triedro de Frenet

${\vec {T}}={\frac {\vec {v}}{|{\vec {v}}|}}={\vec {\jmath }}$

 

${\vec {N}}={\frac {{\vec {a}}_{n}}{a_{n}}}=-{\vec {\imath }}$

 

${\vec {B}}={\vec {T}}\times {\vec {N}}={\vec {k}}$

Radio de curvatura

$R={\frac {|{\vec {v}}|^{2}}{|{\vec {a}}_{n}|}}={\frac {144}{4}}=36$

Centro de curvatura

${\vec {r}}_{c}={\vec {r}}+R{\vec {N}}=32{\vec {\imath }}+48{\vec {\jmath }}-36{\vec {\imath }}=-4{\vec {\imath }}+48{\vec {\jmath }}$

Instante en que pasa por OY

Valor de t

$x=0\qquad \Rightarrow \qquad t=8$

Posición, velocidad y aceleración en t=4

${\vec {r}}=96{\vec {\jmath }}\qquad \qquad {\vec {v}}=-16{\vec {\imath }}+12{\vec {\jmath }}\qquad \qquad {\vec {a}}=-4{\vec {\imath }}$

Componentes intrínsecas de la aceleración

$a_{t}={\frac {{\vec {a}}\cdot {\vec {v}}}{|{\vec {v}}|}}=3.2\qquad \Rightarrow \qquad a_{n}=|{\vec {a}}_{n}|={\sqrt {|{\vec {a}}|^{2}-a_{t}^{2}}}=2.4$

Triedro de Frenet

${\vec {T}}={\frac {\vec {v}}{|{\vec {v}}|}}=-0.8{\vec {\imath }}+0.6{\vec {\jmath }}$

 

${\vec {N}}=-0.6{\vec {\imath }}-0.8{\vec {\jmath }}$

 

${\vec {B}}={\vec {T}}\times {\vec {N}}={\vec {k}}$