Motocicleta en una curva

Enunciado

A la hora de tomar una curva, ¿de qué sirve inclinarse lateralmente?

1. Supongamos que Jorge Lorenzo toma una curva de 150 m de radio a una velocidad de 160 km/h ¿cuánto debe inclinarse en grados respecto a la vertical para no caerse ni a un lado ni al otro?
2. Es sabido que Marc Márquez es capaz de inclinarse más que otros pilotos. Si en esa misma curva Márquez se inclina 60°, ¿a qué velocidad puede pasar por la curva? ¿Cuánto debe valer como mínimo el coeficiente rozamiento estático del neumático sobre el asfalto?
3. Si en esa curva, Pedrosa intenta hacer lo mismo que Jorge y Marc, pero pisa un charco que nadie más ha visto, de forma que el coeficiente de rozamiento estático se reduce a $\mu =0.5$, ¿qué efecto tiene sobre la moto (a) respecto a su trayectoria (b) respecto a su inclinación?

Introducción

Este problema tiene una relación directa con el problema del vuelco de un camión. También con el de la motocicleta que acelera, con la diferencia esencial respecto a ese problema de que aquí debemos considerar una aceleración lateral, mientras que allí era en la dirección de avance.

Este problema puede abordarse de forma intuitiva con ayuda del concepto de fuerza centrífuga. Sin embargo, dado que el tratamiento matemático de las fuerzas de inercia (centrífuga, Coriolis y otras) se escapa al contenido del curso, lo trataremos usando exclusivamente la descripción de la dinámica del sólido en un sistema de referencia inercial.

El problema de la dinámica de una motocicleta (y de una bicicleta) es un tema extremadamente complejo, que se halla aun en estudio. A la hora de considerar el paso por curva influyen factores como la dirección de las ruedas respecto al eje de la moto, la posición del cuerpo del motorista, los movimientos que hace, el cambio de rapidez al recorrer la curva, el posible peralte de la pista, etc.

Por ello, aquí solamente consideraremos el aspecto más elemental, tratando la motocicleta como un sólido con una cierta inclinación respecto a la vertical.

Inclinación dada una velocidad

Cuando el motorista describe una curva, su centro de masas experimenta una aceleración normal hacia el interior de la curva, de valor,

$a_{n}={\frac {M|{\vec {v}}|_{C}^{2}}{R}}$

Para producir esta aceleración debe existir una fuerza actuando en la dirección normal y hacia adentro. Esto se consigue de dos formas: girando la rueda delantera e inclinando el cuerpo. Ambas acciones deben realizarse a la vez, si se quiere evitar la caída.

Si inclina la moto sin girar la rueda delantera, se caerá hacia adentro de la curva. Si gira la rueda sin inclinarse, caerá hacia afuera.

El mecanismo por el que ocurre lo primero es el siguiente: cuando el motorista circula en recta sin inclinar el cuerpo, sobre el actúan el peso y la reacción normal del suelo, sobre la misma recta soporte, por lo que no se produce par. Cuando inclina el cuerpo hacia el interior de la curva, las dos rectas soporte se separan y aparece un par. Este par tiende a girar la moto. En el punto de contacto con el suelo, este par tendería a mover la rueda lateralmente hacia afuera de la curva. Se lo impide el rozamiento. Por ello, aparece una fuerza de rozamiento hacia el interior de la curva. Esta fuerza de rozamiento es normal a la dirección de avance y por ello produce un cambio de dirección. La moto tiende a girar. Si las ruedas no están adaptadas a la nueva trayectoria, el resultado puede ser una caída.

    

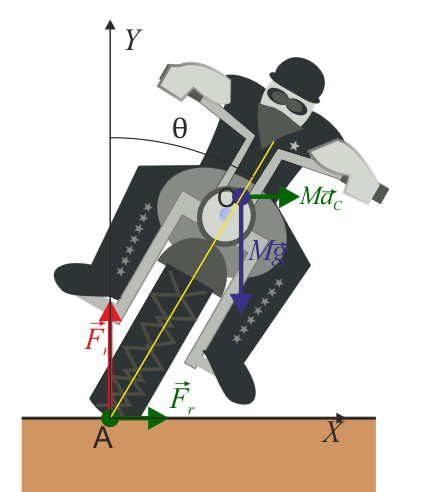
Supongamos que en un instante dado la motocicleta se encuentra describiendo una curva de radio $R$ con velocidad ${\vec {v}}_{C}$. Tomamos como eje OX el instantáneo que pasa por el centro de la circunferencia y el punto de apoyo de la moto. Como eje OY el vertical hacia arriba y como OZ el que sale hacia afuera de la pantalla o el papel. Entonces, si la dirección de avance de la motocicleta es hacia afuera, tenemos

${\vec {v}}_{C}=v_{C}{\vec {k}}\qquad \qquad {\vec {a}}_{C}={\frac {v_{C}^{2}}{R}}{\vec {\imath }}$

El motorista se inclina hacia adentro de la curva, de forma que la línea que va desde el punto de apoyo A hasta el centro de masas forma un ángulo $\theta$ con la vertical, con lo que la posición del CM respecto al punto apoyo es

${\vec {AC}}=h\,\mathrm {sen} (\theta ){\vec {\imath }}+h\cos(\theta ){\vec {\jmath }}$

Sobre la moto, en este plano actúan tres fuerzas:

• El peso $M{\vec {g}}=-Mg{\vec {\jmath }}$
• La reacción normal en A, ${\vec {F}}_{n}=F_{n}{\vec {\jmath }}$
• La fuerza de rozamiento estático en A, ${\vec {F}}_{r}=F_{r}{\vec {\imath }}$

La ecuación de movimiento para el CM queda entonces

$M{\vec {g}}+{\vec {F}}_{n}+{\vec {F}}_{r}=M{\vec {a}}_{C}\qquad \Rightarrow \qquad \left\{{\begin{array}{rlc}F_{r}&=&{\dfrac {Mv_{C}^{2}}{R}}\\&&\\F_{n}-Mg&=&0\end{array}}\right.$

Despejando de aquí

$F_{n}=Mg\qquad \qquad F_{r}={\frac {Mv_{C}^{2}}{R}}$

Si el motorista consigue mantener el equilibrio sin caerse quiere decir que no hay giro respecto al eje Z. Tomando momentos de las fuerzas respecto al CM

${\overrightarrow {CA}}\times {\vec {F}}_{n}+{\overrightarrow {CA}}\times {\vec {F}}_{r}={\vec {0}}$

que nos da la relación

$-F_{n}h\,\mathrm {sen} (\theta )+F_{r}h\,\cos(\theta )=0$

es decir,

$\mathrm {tg} (\theta )={\frac {F_{r}}{F_{n}}}={\frac {v_{C}^{2}}{Rg}}$

Esta es la relación entre el ángulo de inclinación y la velocidad con la que se toma la curva. Es análoga a la que aparece al estudiar el peralte de una curva con la diferencia de que aquí la fuerza normal no la proporciona el peso sino el rozamiento.

Aplicando este resultado a los datos numéricos

$v_{C}=160\,{\frac {\mathrm {km} }{\mathrm {s} }}=44.4\,{\frac {\mathrm {m} }{\mathrm {s} }}\qquad \qquad R=150\,\mathrm {m} \qquad \qquad g=9.81\,{\frac {\mathrm {m} }{\mathrm {s} ^{2}}}$

y resulta

$\mathrm {tg} (\theta )={\frac {44.4^{2}}{150\times 9.81}}=1.34\qquad \Rightarrow \qquad \theta =0.93\,\mathrm {rad} =53.3^{\circ }$

Velocidad dada la inclinación

La relación anterior puede invertirse y hallar la velocidad en función del ángulo

$v_{C}={\sqrt {Rg\,\mathrm {tg} (\theta )}}$

que para un ángulo de 60° da

$v_{C}={\sqrt {150\times 9.81\times 1.732}}\,{\frac {\mathrm {m} }{\mathrm {s} }}=50.5\,{\frac {\mathrm {m} }{\mathrm {s} }}=182\,{\frac {\mathrm {km} }{\mathrm {h} }}$

Vemos como el poderse inclinar 7 grados más le permite alcanzar una velocidad 20km/h mayor.

Efecto de un charco

Existe un límite a lo que se puede inclinar la moto. Lo da el coeficiente de rozamiento estático, ya que la fuerza de rozamiento tiene un máximo. Si se intenta superar ese máximo no hay fuerza suficiente para compensar el par debido al peso y la normal y la motocicleta acaba por tierra.

El límite lo da el que

$\mathrm {tg} (\theta )={\frac {F_{r}}{F_{n}}}\leq \mu$

que para los ejemplos anteriores implica que μ debe ser al menos 1.73 (o 2 o más, para estar seguros). Si de pronto, al pisar el charco el coeficiente de rozamiento cae a un valor muy inferior disminuye la fuerza de rozamiento (la única normal que hay) y de producen dos efectos:

• Al disminuir la aceleración normal, la moto hace “un recto”, saliéndose de la curva.
• Al no poder compensar el par producido por el peso y la fuerza normal, la moto acaba cayendo por el lado interior de la curva.

La combinación de ambos efectos es la que produce la típica imagen de la moto que va arrastrándose hacia el exterior de la curva.