Masa de un sistema de partículas
La masa total del sistema es la suma de las masas de los partículas que lo componen
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle M = m_1 + m_2 + \cdots=\sum_i m_i}
Si el sistema se compone de varias partes, la masa será la suma de las de las partes que lo componen

Densidad de masa
Volumétrica
Cuando tenemos un sistema de muchos millones de partículas (como en un sólido, o un fluido), no es práctico hacer el sumatorio de las masas individuales. En su lugar se divide el sistema en elementos de volumen, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta{}V}
, que son regiones del espacio lo suficientemente pequeñas para tratarlas como diferenciales, pero lo suficientemente grandes como para que contengan miles de partículas. El sistema se considera entonces como continuo, esto es, en lugar de describirse como formado por partículas separadas, se considera constituido por elementos de volumen adyacentes.
Se define entonces la densidad de masa,  , de un elemento de volumen, como la masa de las partículas que lo forman, dividida por el volumen del elemento
, de un elemento de volumen, como la masa de las partículas que lo forman, dividida por el volumen del elemento
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho = \frac{1}{\Delta{}V} \sum_{m_i\in\Delta{}V} m_i}
Dicho de otra forma, la masa de un elemento de volumen es el producto de la densidad de masa por el volumen del elemento
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta m = \sum_{m_i\in\Delta{}V} m_i = \rho\,\Delta{}V}
La masa total del sistema será la suma de la masa de todos sus elementos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle M = \sum_{\forall\ \Delta m} \Delta m = \sum_{\forall\ \Delta{}V} \rho\,\mathrm{\Delta{}V}}
Una suma de muchas cantidades muy pequeñas no es otra cosa que una integral
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}M=\rho\,\mathrm{d}V\qquad\Rightarrow\qquad M = \int_M \mathrm{d}M = \int_V \rho\,\mathrm{d}{}V}
Aquí la densidad es una función de la posición porque en un sistema no homogéneo (por ejemplo, el cuerpo humano) la densidad varía de un punto a otro.
Un material homogéneo es aquel en que sus propiedades son iguales en todos sus puntos. Para este tipo de materiales
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho\neq\rho(\vec{r})\qquad \Rightarrow\qquad \rho=\frac{M}{V}\qquad\qquad M=\rho\,V}
A menudo, un sistema compuesto está formado por varias partes cada una de las cuales es homogénea. En ese caso
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle M=\sum_k \rho_k V_k\,}
En ese caso podemos definir una densidad media como
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho_m=\frac{M}{V}=\dfrac{\sum_k \rho_k V_k}{\sum_k V_k}}
Superficial
Aunque en principio todas las masas ocupan un volumen en el espacio hay ocasiones (una chapa metálica, una hoja de papel,…) en las que se concentran en una superficie de pequeño espesor. En ese caso, se define la densidad superficial de masas
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sigma=\frac{1}{\Delta S}\sum_{m_i\in\Delta S}m_i}
Esta densidad de masa se mide en kg/m² en el SI.
La densidad superficial de masa, como la volumétrica, es una función de la posición, por lo que la masa total será la suma de las de todos los trozos en que se divide la superficie
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}M=\sigma\,\mathrm{d}S\qquad\Rightarrow\qquad M=\int_M\mathrm{d}M=\int_S\sigma\,\mathrm{d}S}
En una superficie de un material homogéneo (y que además tenga el mismo espesor en todos sus puntos)
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sigma\neq\sigma(\vec{r})\qquad \Rightarrow\qquad \sigma=\frac{M}{S}\qquad\qquad M=\sigma\,S}
Lineal
De la misma manera, para hilos y cables, es útil definir la densidad lineal de masa, que se mide en kg/m,
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mu=\frac{1}{\Delta l}\sum_{m_i\in\Delta l}m_i}
de manera que la masa total de un hilo es
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}M=\mu\,\mathrm{d}l\qquad\Rightarrow\qquad M=\int_M\mathrm{d}M=\int_L\mu\,\mathrm{d}l}
Para un hilo homogéneo
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mu\neq\mu(\vec{r})\qquad \Rightarrow\qquad \mu=\frac{M}{L}\qquad\qquad M=\mu\,L}
Centro de masas (CM)
Definición
El centro de masas (CM) de un sistema de partículas es una media ponderada, según la masa individual, de las posiciones de todas las partículas que lo componen
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_G = \frac{m_1\vec{r}_1+m_2\vec{r}_2+\cdots}{m_1+m_2+\cdots} = \frac{m_1\vec{r}_1+m_2\vec{r}_2+\cdots}{M}=\frac{1}{M}\sum_i m_i\vec{r}_i}
o, usando la notación de posiciones relativas
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OG}=\frac{1}{M}\sum_i m_i \overrightarrow{OP}_i}
Equivalentemente se cumple
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle M\vec{r}_G = \sum_im_i\vec{r}_i}
En el caso de un sistema continuo, habrá que sumar para todos los elementos que lo componen
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_G = \frac{1}{M}\int_M \vec{r}\,\mathrm{d}m = \frac{1}{M}\int_V \vec{r}\,\rho\,\mathrm{d}{}V}
El centro de masas siempre ocupará una posición intermedia entre las posiciones de las diferentes partículas del sistema. Así, en un triángulo formado por masas iguales, el centro de masas es el llamado baricentro,que se encuentra siempre en el interior.
No obstante, hay que destacar que el centro de masas de un sistema de partículas no tiene por qué coincidir con ninguna de las partículas que lo componen.

De hecho, en el caso de un sistema sólido, es perfectamente posible que el centro de masas esté fuera del sólido. Por ejemplo, en un salto de altura estilo Fosbury, el atleta pasa por encima del listón, pero su centro de masas pasa por debajo de él (consiguiendo el deportista arrancar así unos cuantos centímetros más en el salto).
Caso de solo dos partículas
Si tenemos solo dos partículas el centro de masas se hallará en una posición intermedia entre ellas.
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OG}=\frac{m_A\overrightarrow{OA}+m_B\overrightarrow{OB}}{m_A+m_B}\qquad\Rightarrow\qquad \overrightarrow{AG}=\overrightarrow{OG}-\overrightarrow{OA}=\frac{m_B}{m_A+m_B}\overrightarrow{AB}}
El CM de las dos masas estará más cerca de la masa más grande. Si las dos masas son iguales se hallará en el punto medio entre ellas.
Sistema compuesto
Si tenemos un sistema formado por varias partes separadas, cada una de ellas tendrá su propio centro de masas
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OG}_k = \frac{1}{M_k}\sum_{m_i\in M_k}m_i\overrightarrow{OP}_i}
El centro de masas del sistema completo equivale a considerar cada parte como una sola partícula ya que
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OG}=\frac{1}{M}\sum_i m_i\overrightarrow{OP}_i = \frac{1}{\sum_k M_k}\sum_k\left(\sum_{m_i\in M_k}m_i\overrightarrow{OP}_i\right) =\frac{\sum_k M_k \overrightarrow{OG}_k}{\sum_k M_k}}
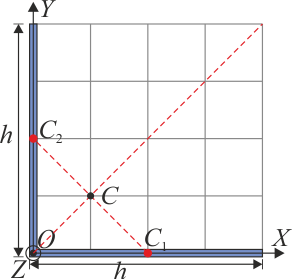
El centro de masas de una L
Así, por ejemplo, en un sistema de dos barras iguales soldadas formando una L, el CM del conjunto se halla en el punto medio de la línea que une los respectivos centros de masa.
El CM del sistema Tierra-Luna
En el sistema Tierra-Luna la proporción entre las masas es 0.0123 y por tanto la posición del CM en el sistema Tierra-Luna se halla en
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{TG}=\frac{0.0123}{1.0123}\overrightarrow{TL}=0.0122\overrightarrow{TL}}
siendo su distancia al centro de la Tierra
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left|\overrightarrow{TG}\right| = 0.0122\times 384000\mathrm{km} = 4670\,\mathrm{km}}
Puesto que el radio de la Tierra es de 6370km, el CM se encuentra en el interior de la Tierra, pero no en su centro. Este detalle es relevante porque no es estrictamente cierto que la Luna de vueltas en torno a la Tierra, sino que lo que ocurre es que ambos astros orbitan en torno al CM común.
Sistema simétrico
Cuando tenemos un sistema que tiene un plano de simetría, el CM del sistema se halla en dicho plano, ya que las coordenadas perpendiculares a dicho plano se cancelan entre partículas simétricas.
Si tiene dos planos de simetría, el CM se hallará en la recta intersección de dichos planos.
Si teien tres planos de simetría que se cortan en un solo punto (caso de una esfera, o de un prisma rectangular, por ejemplo), dicho punto es el CM.
Sistema de referencia del centro de masas
El sistema de referencia ligado al CM, que tiene su origen en este punto y que se traslada con él se denomina sistema centro de masas. Las posiciones de las partículas en este sistema son las relativas al CM
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle {\vec{r}_i}^{\,\prime} = \vec{r}_i-\vec{r}_G\qquad\qquad \overrightarrow{GP}_i=\overrightarrow{OP}_i-\overrightarrow{OG}}
Dado que la posición del centro de masas respecto a sí mismo es evidentemente nula, se cumple
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{0}=\vec{r}^{\,\prime}_G \qquad \Rightarrow\qquad \sum_im_i\vec{r}^{\,\prime}_i=m_1\vec{r}^{\,\prime}_1+m_2\vec{r}^{\,\prime}_2 +\cdots = \vec{0}\qquad\qquad \sum_im_i \overrightarrow{GP}_i=\vec{0}}



