Principio de los Trabajos Virtuales
Ligaduras ideales
Un sistema mecánico está sometido a ligaduras ideales si, en un desplazamiento virtual, el trabajo total realizado por las fuerzas de ligadura es nulo:
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta W_{lig} = \sum\limits_{i} \vec{\Phi}_i\cdot\delta\vec{r}_i=0. }
El sumatorio se extiende a todas las fuerzas de ligadura que actúen sobre el sistema. Esta condición se cumple para un gran número de sistemas mecánicos. Es importante comprender que aunque haya rozamiento las ligaduras pueden ser ideales. Veamos algunos ejemplos.
Sistemas con vínculos lisos: en este caso las fuerzas de ligadura son perpendiculares a las superficies de contacto. Entonces, en un desplazamiento virtual del sistema las fuerzas vinculares son siempre perpendiculares a los desplazamientos y no hacen trabajo.
Sistemas con vínculos rugosos estáticos: ocurre cuando la fuerza de rozamiento entre dos superficies es tan grande que es imposible que haya movimiento relativo entre ellas. Entonces, este movimiento de deslizamiento relativo está prohibido en un desplazamiento virtual y la fuerza de rozamiento no hace trabajo.
Rodadura sin deslizamiento. Para que haya rodadura sin deslizamiento es necesario que exista rozamiento. Pero el punto de contacto entre los sólidos no tiene movimiento de deslizamiento. Entonces, la fuerza de rozamiento no hace trabajo sobre ese punto en un deslizamiento virtual y la ligadura es ideal.
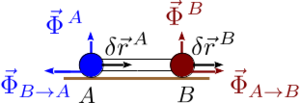
Vínculo interno de rigidez en sólidos rígidos. En este caso, cada una de las fuerzas de ligadura realiza un trabajo no nulo en un desplazamiento virtual, pero el trabajo total de ligadura es nulo. El sólido rígido de la figura está compuesto por dos partículas unidas por una barra rígida sin masa. El sólido se apoya en una superficie horizontal. En un desplazamiento virtual tenemos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta\vec{r}^{\,A} = \delta\vec{r}^{\,B}. }
Las fuerzas de ligadura que actúan sobre cada partícula se indican en la figura con el mismo color de la partícula. El trabajo total de ligadura en un desplazamiento virtual es
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta W_{lig} = (\vec{\Phi}^{\,A}+\vec{\Phi}_{B\to A})\cdot\delta\vec{r}^{\,A} + (\vec{\Phi}^{\,B}+\vec{\Phi}_{A\to B})\cdot\delta\vec{r}^{\,B} = \vec{\Phi}_{B\to A}\cdot\delta\vec{r}^{\,A} + \vec{\Phi}_{A\to B}\cdot\delta\vec{r}^{\,B} = ( \vec{\Phi}_{B\to A}+\vec{\Phi}_{A\to B})\cdot\delta\vec{r}^{\,A} = \vec{0}. }
En el último paso hemos usado que, por la Tercera Ley de Newton, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\Phi}_{B\to A} = - \vec{\Phi}_{A\to B}} .
Algunos ejemplos de ligaduras no ideales son: desplazamiento relativo de superficies con rozamiento y la presencia de vínculos unilaterales.
Enunciado del Principio de los Trabajos Virtuales (P.T.V.)
|
Un sistema de partículas que esté sometido a ligaduras ideales está en equilibrio si y sólo si el trabajo total realizado por las fuerzas aplicadas sobre el sistema es nulo en cualquier desplazamiento virtual del sistema Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta W = \sum\limits_{i} \vec{F}_i\cdot\delta\vec{r}_i=0. } |
El sumatorio se extiende a todas las fuerzas aplicadas que actúen sobre el sistema.
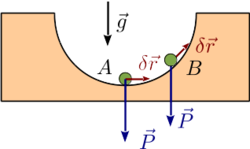
La figura de la derecha muestra una aplicación sencilla de este principio. Aquí la fuerza aplicada es el peso de la partícula. El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} no es un punto de equilibrio, pues en el desplazamiento virtual indicado en la figura el peso realiza trabajo. El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} si es de equilibrio, pues cualquier desplazamiento virtual es perpendicular al peso y, por tanto, el peso no realiza trabajo.
El P.T.V. puede demostrarse a partir de la Segunda Ley de Newton. Para que un sistema de partículas esté en equilibrio debe ocurrir que la fuerza neta sobre cada partícula sea nula
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_i + \vec{\Phi}_i=\vec{0}\qquad \forall i. }
Aquí, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_i} es la fuerza aplicada neta sobre la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i} , mientras que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\Phi}_i} es la fuerza de ligadura neta sobre la partícula. Multiplicando la expresión por un desplazamiento virtual arbitrario de la partícula Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta\vec{r}_i} tenemos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (\vec{F}_i + \vec{\Phi}_i)\cdot\delta\vec{r}_i=0\qquad \forall i. }
Si sumamos para todas las partículas tenemos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sum\limits_{i=1}^N(\vec{F}_i + \vec{\Phi}_i)\cdot\delta\vec{r}_i=0 \Longrightarrow \sum\limits_{i=1}^N\vec{F}_i\cdot\delta\vec{r}_i + \sum\limits_{i=1}^N\vec{\Phi}_i\cdot\delta\vec{r}_i=0 \Longrightarrow \sum\limits_{i=1}^N\vec{F}_i\cdot\delta\vec{r}_i =0 }
En el último paso hemos usado que las ligaduras del sistema son ideales.
P.T.V. para sólidos rígidos
En un sistema de sólidos rígidos los movimientos pueden ser traslaciones y/o rotaciones. Además, las acciones externas se describen en términos de fuerzas y pares de fuerzas. Es por ello que el enunciado para sólidos rígidos se particulariza así:
| Un sistema de sólidos rígidos sometido a ligaduras ideales está en equilibrio sí y sólo si el trabajo total realizado por las fuerzas y momentos aplicados sobre el sistema es nulo en cualquier desplazamiento virtual del sistema.
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta W = \sum\limits_{i} \vec{F}_i\cdot\delta\vec{r}_i + \sum\limits_{j}\vec{M}_j\cdot\delta\vec{\theta}_j =0. } |
Aquí, el sumatorio en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i} se extiende a todas las fuerzas aplicadas que actúen sobre el sistema, y el sumatorio en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle j} a todos los momentos aplicados. En cada caso, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta\vec{r}_i} es el desplazamiento virtual del punto donde se aplica la fuerza Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_i} , mientras que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta\vec{\theta}_j} es la rotación virtual del sólido al que se aplica el par de fuerzas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{M}_j} . Cabe destacar que este enunciado es también valido para sistemas de partículas. Si no hay sólidos rígidos en el sistema el término con los momentos y las rotaciones no aparece.
Veamos una aplicación sencilla de este principio. La barra de la derecha está articulada en su punto central, de modo que ese punto es fijo y la barra puede realizar una rotación plana alrededor de un eje perpendicular a ella y que pasa por Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} . Se aplica un fuerza Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}} en el extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} como se indica en la figura. ¿Qué par de fuerzas hay que aplicar para que la barra no rote?
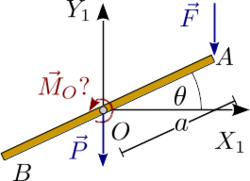
Las fuerzas aplicadas son Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}} en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} y el peso en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} . El par buscado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{M}_O} es también aplicado. El sistema tiene un grado de libertad: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\theta\}} . Por tanto un desplazamiento virtual es descrito como Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\delta\theta\}} . Este desplazamiento virtual propicia una rotación virtual del sólido y un desplazamiento virtual del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} . La rotación virtual se expresa
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta\vec{\theta} = \delta\theta\,\vec{k}_1. }
El vector de posición de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} es
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_A = a\,(\cos\theta\,\vec{\imath}_1 + \mathrm{sen}\,\theta\,\vec{\jmath}_1), }
y su desplazamiento virtual es
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta\vec{r}_A = \left(\dfrac{\partial\vec{r}_A}{\partial\theta}\right) = a\delta\theta\,(-\,\mathrm{sen}\,\theta\,\vec{\imath}_i + \cos\theta\,\vec{\jmath}_1). }
El punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} no se mueve en el desplazamiento virtual: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta\vec{r}_O=\vec{0}} . Las fuerzas y momentos aplicados son
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F} = -F_0\,\vec{\jmath}_1, \qquad \vec{P} = -P\,\vec{\jmath}_1, \qquad \vec{M}_O = M_O\,\vec{k}_1. }
El trabajo total realizado por las fuerzas y momentos aplicados en el desplazamiento virtual es
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta W = \vec{F}\cdot\delta\vec{r}_A + \vec{P}\cdot\delta\vec{r}_O + \vec{M}_O\cdot\delta\vec{\theta}= (-aF\cos\theta+M_O)\,\delta\theta=0 }
Como tiene que ser cero para cualquier valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta\theta} , obtenemos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle M_O = aF\cos\theta \Longrightarrow \vec{M}_O = aF\cos\theta\,\vec{k}_1. }
Principio de las Potencias Virtuales (P.P.V.)
Esta es una formulación alternativa del P.T.V. en el que se usan las velocidades virtuales en vez de los desplazamientos y rotaciones virtuales.
Para un sistema de partículas es
|
Un sistema de partículas que esté sometido a ligaduras ideales está en equilibrio si y sólo si la potencial total realizada por las fuerzas aplicadas sobre el sistema es nulo en cualquier desplazamiento virtual del sistema Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta W = \sum\limits_{i} \vec{F}_i\cdot\delta\vec{v}^{\,*}_i=0. } |
En el caso de solidos rígidos tenemos
| Un sistema de sólidos rígidos sometido a ligaduras ideales está en equilibrio sí y sólo si la potencia virtual realizada por las fuerzas y momentos aplicados sobre el sistema es nula en cualquier desplazamiento virtual del sistema.
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \delta W = \sum\limits_{i} \vec{F}_i\cdot\delta\vec{v}^{\,*}_i + \sum\limits_{j}\vec{M}_j\cdot\delta\vec{\omega}^{\,*}_j =0. } |
