Coordenadas generalizadas
Partícula puntual

Consideremos el sistema mecánico mas sencillo posible: un partícula puntual libre de masa . Usando coordenadas cartesianas la posición de la partícula en cada instante de tiempo puede describirse usando su vector de posición respecto a un cierto sistema de ejes coordenados:
Que la partícula sea libre significa que las tres coordenadas pueden tomar cualquier valor independientemente de las otras. Entonces, no hay ningún movimiento prohibido para la partícula, como se indica en la figura. El número de grados de libertad es 3.
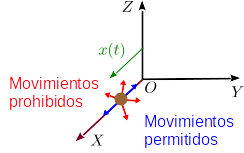
Supongamos ahora que la partícula está obligada a moverse en el eje .Podemos imaginar que la partícula es una cuenta engarzada en un alambre recto y hacemos coincidir el eje con el alambre. Esto significa que, no importa la fuerza que ejerzamos sobre la partícula, esta no puede salirse del hilo. Cualquier movimiento que la saque del hilo está prohibido. Se dice entonces que la partícula está vinculada o ligada. Entonces, no necesitamos las tres coordenadas cartesianas para determinar la posición de la partícula. Sabemos que se cumplirá siempre y : estas condiciones se llaman ligaduras o vínculos. La partícula tiene un grado de libertad y podemos elegir como coordenada . El vector de posición sería
Físicamente, para que la partícula respete la ligadura es necesario que el vínculo (en este caso el hilo) ejerza sobre la partícula la fuerza necesaria para que ésta no se salga del hilo cuando otras fuerzas actúan sobre ella. Estas son las fuerzas de ligadura. Su magnitud es desconocida antes de resolver el problema, es decir, es una incógnita (no un grado de libertad). Sí tenemos información previa sobre su dirección. Si el vínculo es liso, la fuerza de ligadura es perpendicular al vínculo. Si es rugoso, tendrá una componente normal al vínculo (en este caso, para que la partícula no se salga del hilo) y otra tangencial, la fuerza de rozamiento.

Supongamos que el hilo es circular, de radio y situado en el plano . El vector de posición de la partícula es
Vemos dos coordenadas en el vector: , pero la partícula tiene sólo un grado de libertad. Lo que ocurre es que estas coordenadas no pueden variar de forma independiente. Tienen que cumplir la ligadura . Podríamos escoger o para especificar la posición de la partícula y despejar la otra a partir de la condición de ligadura. Pero en este caso es mas conveniente escoger el ángulo de la figura como coordenada: . De esta forma el vector de posición es
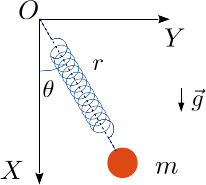
En la figura de la derecha tenemos un péndulo plano en el que la cuerda ha sido sustituida por un muelle. La partícula tiene dos grados de libertad. Podemos expresar el vector de posición en función de y
El número de grados de libertad es 2 y las coordenadas usadas son .
En este último caso hemos usado un ángulo y una distancia para describir la posición de la partícula, aunque sean magnitudes cualitativamente distintas. Este es el concepto de coordenadas generalizadas: son cualesquiera magnitudes que puedan utilizarse para describir un sistema. En este curso serán distancias y/o ángulos, pero en general puede ser cualquier cosa: una componente de momento de una fuerza, un índice bursátil, etc.
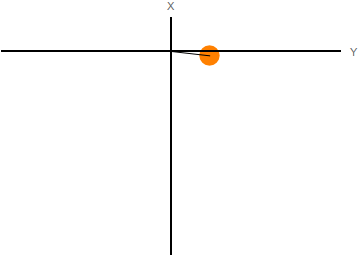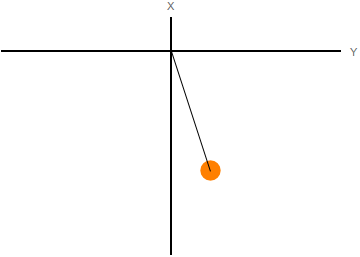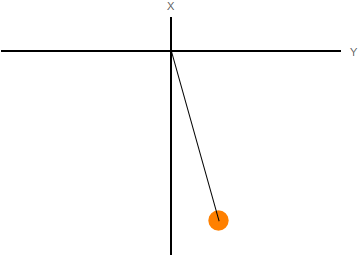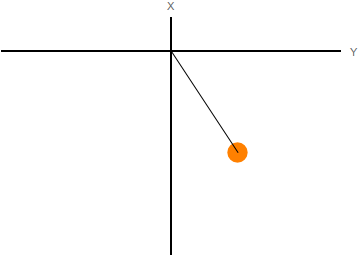
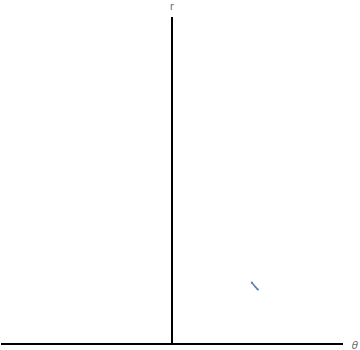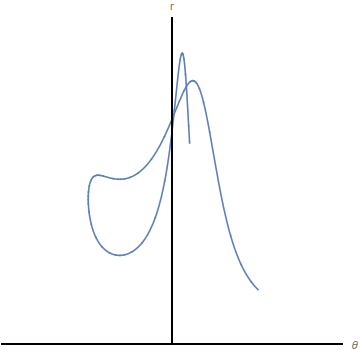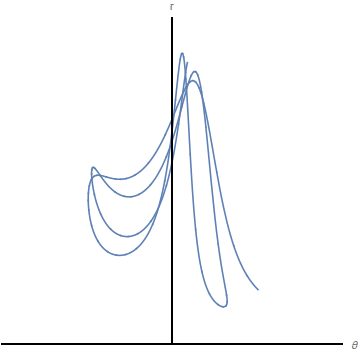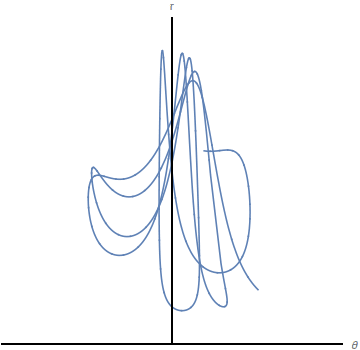
El espacio de configuraciones es el generado por las coordenadas generalizadas. El movimiento del sistema puede visualizarse como el movimiento de un punto que representa al sistema en el espacio de las configuraciones. En la figura de la izquierda representamos el movimiento del péndulo con muelle del último ejemplo en el espacio real. A la derecha se representa el movimiento de la masa en el espacio de las configuraciones.
 |
 |
Sistemas de partículas: Sólido Rígido
Si tenemos un sistema con partículas, tendremos vectores de posición y, por tanto, coordenadas cartesianas. Si las partículas tienen que cumplir ligaduras, el número de grados de libertad es . Necesitaremos entonces coordenadas generalizadas, , para describir en cada instante la configuración del sistema.
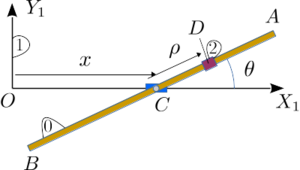
En el caso de un sólido rígido libre ya hemos visto que se necesitan 6 coordenadas para describir su posición: 3 coordenadas asociadas a la traslación y 3 a la rotación. Aunque un sólido tiene muchos puntos, la condición de rigidez impone condiciones muy restrictivas al movimiento, resultando en 6 grados de libertad para el sólido rígido libre. En el caso de sólidos vinculados habrá que examinar cada sistema individualmente. Por ejemplo, el sistema de la figura, formado por dos sólidos vinculados (la barra "0" y el deslizador "2") tiene 3 grados de libertad




























