Fuerza sobre una barra

Enunciado

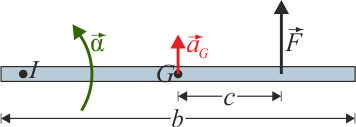
Sobre una barra de longitud $b$ y masa $M$ situada en reposo horizontalmente en una superficie sin rozamiento se aplica una fuerza $F_{0}$ también horizontal. El punto de la aplicación se encuentra a una distancia $c$ del centro de la barra.

1. Si la fuerza es perpendicular a la barra, ¿cuánto valen la aceleración del CM y la aceleración angular de la barra? ¿Alrededor de qué punto comienza a girar la barra?
2. Suponga ahora que la fuerza forma un ángulo $\beta$ con la barra, ¿cuánto valen ese caso las aceleraciones y donde se encuentra el centro instantáneo de rotación?
3. Suponga que la barra se encuentra articulada en un extremo de forma que sólo puede girar en torno a este punto. ¿Cuánto valen las aceleraciones en ese caso? ¿Cuánto vale la fuerza que el punto de articulación ejerce sobre la barra?
4. Si la barra estuviera empotrada en su extremo, de forma que no pudiera moverse de ninguna manera, ¿cuánto valdrían la fuerza y el momento de reacción ejercidos por el soporte?

Aceleraciones

Aceleración lineal del centro de masas

La aceleración del centro de masas la calculamos aplicando el teorema de la cantidad de movimiento

$M{\vec {a}}_{G}={\vec {F}}$

siendo ${\vec {F}}$ la resultante de todas las fuerzas externas aplicadas sobre el sólido. En nuestro caso, si situamos el origen de coordenadas en el centro de la barra y el eje OX a lo largo de ella, tenemos

${\vec {F}}=F_{0}{\vec {\jmath }}$

Técnicamente, a esta fuerza deberíamos añadir el peso de la barra y la reacción de la superficie horizontal, pero estas dos se anulan mutuamente.

Esto nos da la aceleración

${\vec {a}}_{G}={\frac {\vec {F}}{M}}={\frac {F_{0}}{M}}{\vec {\jmath }}$

Aceleración angular

La aceleración angular del movimiento alrededor del CM la hallamos aplicando el teorema del momento cinético

${\frac {\mathrm {d} {\vec {L}}_{G}}{\mathrm {d} t}}={\vec {M}}_{G}$

siendo ${\vec {M}}_{G}$ la resultante de los momentos respecto al CM de las diferentes fuerzas externas aplicadas

${\vec {M}}_{G}=\sum _{i}{\overrightarrow {GP}}_{i}\times {\vec {F}}_{i}$

En nuestro caso tenemos el peso y la reacción normal, que son opuestas se aplican en el mismo punto y por tanto se cancelan, y el de la fuerza ${\vec {F}}_{0}$, cuyo momento vale

${\vec {M}}_{G}=\left(c{\vec {\imath }}\right)\times (F_{0}{\vec {\jmath }})=cF_{0}{\vec {k}}$

El momento de inercia respecto a un eje perpendicular a la varilla y que pasa por su centro de masas es

$I={\frac {1}{12}}Mb^{2}$

lo que nos da la aceleración angular

$I{\vec {\alpha }}={\vec {M}}_{G}\qquad \Rightarrow \qquad {\vec {\alpha }}={\frac {12F_{0}c}{Mb^{2}}}{\vec {k}}$

Esta aceleración angular se anula si $c=0$, es decir, si empujamos la barra justamente en su centro, ésta no gira, solo se traslada.

Centro instantáneo de rotación

La barra no comienza a girar alrededor de su centro, ya que a la vez se está trasladando. Realiza un movimiento en el plano horizontal alrededor de un centro instantáneo de rotación, que será diferente en cada momento.

Puesto que parte del reposo, la velocidad del centro y la velocidad angular será en los primeros instantes

${\vec {v}}_{G}={\vec {a}}_{G}t={\frac {F_{0}}{M}}t{\vec {\jmath }}\qquad \qquad {\vec {\omega }}={\vec {\alpha }}t={\frac {12F_{0}c}{Mb^{2}}}t{\vec {k}}$

La posición del CIR respecto al centro de masas es

${\overrightarrow {GI}}={\frac {{\vec {k}}\times {\vec {v}}_{G}}{\omega }}=-{\frac {F_{0}t/M}{12F_{0}ct/Mb^{2}}}{\vec {\imath }}=-{\frac {b^{2}}{12c}}{\vec {\imath }}$

Este CIR se encuentra sobre la recta de la barra pero en un punto que depende de solamente de la longitud de la barra y del punto de aplicación. Nunca se halla en el propio centro de la barra, esto es, con una sola fuerza no podemos conseguir que la barra se limite a rotar sobre su centro; necesitamos un par de fuerzas para ello.

Para que empiece a girar alrededor de su extremo debe resultar una posición del CIR en

${\overrightarrow {GI}}=-{\frac {b}{2}}{\vec {\imath }}\qquad \Rightarrow \qquad c={\frac {b}{6}}$

es decir, para conseguir que gire alrededor de un extremo no hay que empujarla en el otro, sino en un punto a 1/3 del otro extremo.

Fuerza oblicua

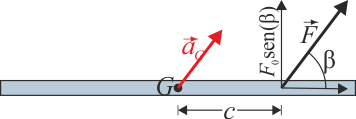
Cuando se aplica una fuerza oblicua, ya entra en juego el ángulo que aparece en el producto vectorial. La fuerza aplicada es ahora

${\vec {F}}_{0}=F_{0}\left(\cos(\beta ){\vec {\imath }}+\mathrm {sen} (\beta ){\vec {\jmath }}\right)$

De aquí resulta una aceleración del CM que es también oblicua

${\vec {a}}_{G}={\frac {\vec {F}}{M}}={\frac {F_{0}}{M}}\left(\cos(\beta ){\vec {\imath }}+\mathrm {sen} (\beta ){\vec {\jmath }}\right)$

Para la aceleración angular, el nuevo momento de la fuerza vale

${\vec {M}}_{G}=(c{\vec {\imath }})\times \left(F_{0}\left(\cos(\beta ){\vec {\imath }}+\mathrm {sen} (\beta ){\vec {\jmath }}\right)\right)=F_{0}c\,\mathrm {sen} (\beta ){\vec {k}}$

Podemos leer este resultado de dos maneras diferentes:

• La fuerza aplicada tiene una componente longitudinal, paralela a la barra, y una transversal, perpendicular a ella. La longitudinal produce desplazamiento a lo largo de la barra, pero no rotación. Por tanto, sólo la componente normal produce rotación y es la única que aparece en el momento de las fuerzas.
• La cantidad relevante a la hora de calcular el momento respecto a un punto no es su distancia al punto de aplicación, sino la distancia a la recta sobre la que actúa la fuerza. Esta distancia es la que se denomina el “brazo del par” y se mide sobre la perpendicular a la recta soporte. Aplicando trigonometría se ve que esta distancia mide $c\,\mathrm {sen} (\beta )$. De ahí que el momento de la fuerza valga $F_{0}c\,\mathrm {sen} (\beta )$

    

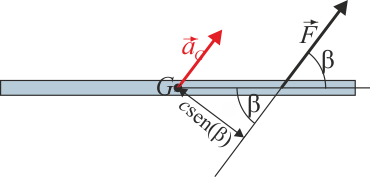
La aceleración angular que adquiere la barra es ahora

$I{\vec {\alpha }}={\vec {M}}_{G}\qquad \Rightarrow \qquad {\vec {\alpha }}={\frac {12cF_{0}\,\mathrm {sen} (\beta )}{Mb^{2}}}{\vec {k}}$

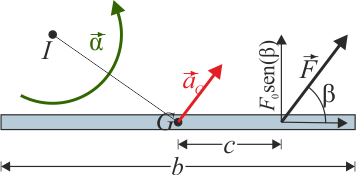
La posición del centro instantáneo de rotación en el instante inicial es ahora

${\overrightarrow {GI}}={\frac {{\vec {k}}\times {\vec {v}}_{G}}{\omega }}=-{\frac {F_{0}t/M}{12F_{0}ct\,\mathrm {sen} (\beta )/Mb^{2}}}\left(\mathrm {sen} (\beta ){\vec {\imath }}-\cos(\beta ){\vec {\jmath }}\right)=-{\frac {b^{2}}{12c}}\left({\vec {\imath }}-\mathrm {cotg} (\beta ){\vec {\jmath }}\right)$

Este CIR se encuentra sobre la recta perpendicular a la velocidad del centro de masas (y a la fuerza aplicada, en este caso).

Barra articulada

Cuando la barra está articulada por su extremo, aparece un vínculo: la velocidad de este punto es nula en todo momento, y el eje de rotación va a pasar siempre por él.

Físicamente, esto corresponde a que en la articulación, el soporte ejerce una fuerza de reacción sobre la barra, que impide que ésta se separe del anclaje.

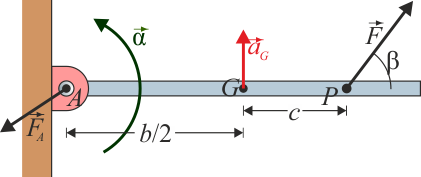
Si etiquetamos como A al punto de articulación y ${\vec {F}}_{A}$ la fuerza de reacción ejercida en este punto, los teoremas de la cantidad de movimiento y del momento cinético quedan ahora

$M{\vec {a}}_{G}={\vec {F}}+{\vec {F}}_{A}\qquad \qquad I{\vec {\alpha }}={\overrightarrow {GP}}\times {\vec {F}}+{\overrightarrow {GA}}\times {\vec {F}}_{A}$

El problema es que ${\vec {F}}_{A}$ es también una incógnita del problema, por lo que con las ecuaciones anteriores no nos bastan para determinar la aceleración de la barra. Necesitamos además la ecuación que describe el vínculo. El hecho de que A es un punto fijo se puede expresar de muchas formas. La más simple es por supuesto

${\vec {v}}_{A}={\vec {0}}$

Al tratarse A de un punto fijo podemos calcular el momento de las fuerzas respecto al punto A, en vez del centro de masas. En este caso, el teorema del momento cinético queda

$I_{A}{\vec {\alpha }}={\overrightarrow {AP}}\times {\vec {F}}+{\overrightarrow {AA}}\times {\vec {F}}_{A}={\overrightarrow {AP}}\times {\vec {F}}$

Vemos que de esta forma desaparece la fuerza de reacción y podemos hallar la aceleración angular. En esta ecuación $I_{A}$ es el momento de inercia respecto a un eje que pasa por A. Por el teorema de Steiner este momento vale

$I_{A}=I_{G}+Md^{2}={\frac {1}{12}}Mb^{2}+M\left({\frac {b}{2}}\right)^{2}={\frac {1}{3}}Mb^{2}$

y el momento de la fuerza aplicada es ahora

${\vec {M}}_{A}={\overrightarrow {AP}}\times {\vec {F}}=\left({\frac {b}{2}}+c\right)F_{0}\mathrm {sen} (\beta ){\vec {k}}$

lo que nos da la aceleración angular

${\vec {\alpha }}={\frac {{\vec {M}}_{A}}{I_{A}}}={\frac {3(b/2+c)F_{0}}{MH^{2}}}\mathrm {sen} (\beta ){\vec {k}}$

Una vez que tenemos la aceleración angular, hallamos la lineal del centro de masas. este punto describe un movimiento circular en torno al punto A, por lo que

${\vec {a}}_{G}={\vec {\alpha }}\times {\overrightarrow {AG}}+{\vec {\omega }}\times \left({\vec {\omega }}\times {\overrightarrow {AG}}\right)$

En el instante inicial, que es el único que nos interesa, la velocidad angular es nula, por lo que queda solo el primer término

${\vec {a}}_{G}={\vec {\alpha }}\times {\overrightarrow {AG}}=\left({\frac {3(b/2+c)}{b^{2}}}F_{0}\mathrm {sen} (\beta ){\vec {k}}\right)\times \left({\frac {b}{2}}{\vec {\imath }}\right)={\frac {3(b/2+c)F_{0}}{2MH}}\mathrm {sen} (\beta ){\vec {\jmath }}$

La fuerza de reacción en la articulación no es la opuesta a la aplicada, pues la barra se está acelerando. Despejando en el teorema de la cantidad de movimiento

${\vec {F}}_{A}=M{\vec {a}}_{G}-{\vec {F}}$

Sustituyendo la aceleración y la fuerza

${\vec {F}}_{A}={\frac {3(b/2+c)F_{0}}{2b}}\mathrm {sen} (\beta ){\vec {\jmath }}-F_{0}\cos(\beta ){\vec {\imath }}-F_{0}\mathrm {sen} (\beta ){\vec {\jmath }}$

Agrupando términos

${\vec {F}}_{A}=-F_{0}\cos(\beta ){\vec {\imath }}-F_{0}\mathrm {sen} (\beta )\left({\frac {b-6c}{4b}}\right){\vec {\jmath }}$

Tal como dijimos antes, si la fuerza se aplica a una distancia de 1/3 del extremo (1/6 desde el centro de la barra), se produce rotación en torno al extremo sin que sea necesaria una fuerza adicional. Por eso, para este valor la fuerza de reacción se anula cuando $\beta =\pi /2$.

Barra empotrada

Si la barra está completamente inmovilizada en su extremo, el vínculo no solo ejerce una fuerza que impide que el extremo se desplace, también ejerce un momento que impide que gire. El mecanismo físico por el cual se ejerce este momento es mediante las fuerzas diferentes que se ejercen en los diferentes puntos del empotramiento. La combinación de estas fuerzas no solo produce una fuerza de reacción, sino también un momento de reacción ${\vec {M}}_{R}$.

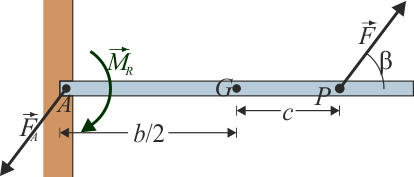
Las ecuaciones para la cantidad de movimiento y el momento cinético quedan ahora

$M{\vec {a}}_{G}={\vec {F}}+{\vec {F}}_{A}\qquad \qquad I_{A}{\vec {\alpha }}={\vec {M}}_{R}+{\overrightarrow {AP}}\times {\vec {F}}$

pero, puesto que el empotramiento obliga a la barra a estar en reposo, las aceleraciones son nulas

${\vec {a}}_{G}={\vec {0}}\qquad \qquad {\vec {\alpha }}={\vec {0}}$

y por tanto la fuerza de reacción vale

${\vec {F}}_{A}=-{\vec {F}}=-F_{0}\left(\cos(\beta ){\vec {\imath }}+\mathrm {sen} (\beta ){\vec {\jmath }}\right)$

y el momento de reacción

${\vec {M}}_{R}=-{\overrightarrow {AP}}\times {\vec {F}}=-\left({\frac {b}{2}}+c\right)F_{0}\mathrm {sen} (\beta ){\vec {k}}$