Estudio analítico de dos masas unidas por un muelle

Enunciado

Como en el problema “Dos masas unidas por un muelle” tenemos dos masas $m_{1}$ y $m_{2}$ se mueven a lo largo del eje OX unidas por un resorte de constante $k$ y longitud natura $\ell _{0}$. Inicialmente las dos masas se encuentran en reposo en $x_{10}=0$ y $x_{20}=\ell _{0}$. Entonces se le comunica a la masa $m_{1}$ una velocidad $v_{0}$ en el sentido positivo del eje.

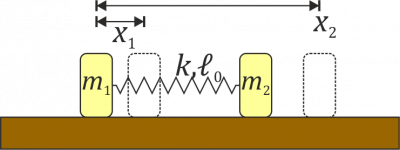
1. Determine la lagrangiana del sistema en función de las posiciones de las dos partículas.
2. Obtenga las ecuaciones de movimiento para $x_{1}$ y $x_{2}$

Realice el cambio de variables a las coordenadas generalizadas $x_{G}=(m_{1}x_{1}+m_{2}x_{2})/(m_{1}+m_{2})$, $x=x_{2}-x_{1}-\ell _{0}$.

3. ¿Cómo queda la lagrangiana en función de estas coordenadas?
4. Obtenga las ecuaciones de movimiento para $x_{G}$ y $x$.
5. Determine dos constantes de movimiento para este sistema.

Lagrangiana en función de x₁ y x₂

Energía cinética

Las dos partículas describen un movimiento rectilíneo, por lo que la energía cinética es simplemente

$T={\frac {1}{2}}m_{1}{\dot {x}}_{1}^{2}+{\frac {1}{2}}m_{2}{\dot {x}}_{2}^{2}$

Energía potencial

Esta es la elástica debida a la elongación del resorte

$U={\frac {1}{2}}k(x_{2}-x_{1}-\ell _{0})^{2}$

Lagrangiana

Restamos las dos cantidades anteriores

${\mathcal {L}}=T-U={\frac {1}{2}}m_{1}{\dot {x}}_{1}^{2}+{\frac {1}{2}}m_{2}{\dot {x}}_{2}^{2}-{\frac {1}{2}}k(x_{2}-x_{1}-\ell _{0})^{2}$

Ecuaciones de movimiento para x₁ y x₂

Aplicamos la ecuación de Lagrange a cada una de las coordenadas

Para la coordenada x₁

Tenemos que

$p_{1}={\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}_{1}}}=m_{1}{\dot {x}}_{1}\qquad \qquad {\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}_{1}}}\right)=m_{1}{\ddot {x}}_{1}$

y

${\frac {\partial {\mathcal {L}}}{\partial {x}_{1}}}=k(x_{2}-x_{1}-\ell _{0})$

lo que da

$m_{1}{\ddot {x}}_{1}=k(x_{2}-x_{1}-\ell _{0})$

Para la coordenada x₂

De la misma manera

$p_{2}={\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}_{2}}}=m_{2}{\dot {x}}_{2}\qquad \qquad {\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}_{2}}}\right)=m_{2}{\ddot {x}}_{2}$

y

${\frac {\partial {\mathcal {L}}}{\partial {x}_{2}}}=-k(x_{2}-x_{1}-\ell _{0})$

lo que nos da

$m_{2}{\ddot {x}}_{2}=-k(x_{2}-x_{1}-\ell _{0})$

Estas son las mismas ecuaciones a las que se llega de forma simple partiendo de la segunda ley de Newton.

Lagrangiana en función de x y x_G

Ninguna de las dos coordenadas es cíclica, ya que ambas aparecen en la energía potencial. Esto produce como resultado dos ecuaciones diferenciales acopladas.

Podemos separarlas mediante el cambio de variables sugerido. Si hacemos

$x=x_{2}-x_{1}-\ell _{0}\qquad \qquad x_{G}={\frac {m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}}$

las coordenadas originales se escriben en función de las nuevas como

$x_{1}=x_{G}-{\frac {m_{2}(x+\ell _{0})}{m_{1}+m2}}\qquad x_{2}=x_{G}+{\frac {m_{1}(x+\ell _{0})}{m_{2}+m_{2}}}$

y las velocidades

${\dot {x}}_{1}={\dot {x}}_{G}-{\frac {m_{2}}{m_{1}+m2}}{\dot {x}}\qquad {\dot {x}}_{2}={\dot {x}}_{G}+{\frac {m_{1}}{m_{2}+m_{2}}}{\dot {x}}$

Llevando esto a la energía cinética, tras operar nos queda

$T={\frac {1}{2}}(m_{1}+m_{2}){\dot {x}}_{G}^{2}+{\frac {m_{1}m_{2}}{2(m_{1}+m_{2})}}{\dot {x}}^{2}$

que podemos leer como un caso particular del teorema de König para la energía cinética.

En cuanto a la potencial, su nueva expresión es

$U={\frac {1}{2}}kx^{2}$

lo que nos da la lagrangiana

${\mathcal {L}}={\frac {1}{2}}(m_{1}+m_{2}){\dot {x}}_{G}^{2}+{\frac {m_{1}m_{2}}{2(m_{1}+m_{2})}}{\dot {x}}^{2}-{\frac {1}{2}}kx^{2}$

Ecuaciones de movimiento para x y x_G

Para la coordenada x_G

$p_{G}={\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}_{G}}}=(m_{1}+m_{2}){\dot {x}}_{G}\qquad \qquad {\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}_{G}}}\right)=(m_{1}+m_{2}){\ddot {x}}_{G}$

y

${\frac {\partial {\mathcal {L}}}{\partial {x}_{G}}}=0$

lo que da

$(m_{1}+m_{2}){\ddot {x}}_{G}=0$

Para la coordenada x

De la misma manera

$p={\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}{\dot {x}}\qquad \qquad {\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {x}}}}\right)={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}{\ddot {x}}$

y

${\frac {\partial {\mathcal {L}}}{\partial {x}}}=-kx$

lo que nos da

${\frac {m_{1}m_{2}}{m_{1}+m_{2}}}{\ddot {x}}=-kx$

Ahora sí resultan ecuaciones desacopladas, cada una de las cuales puede integrarse por separado. La primera es trivial

${\ddot {x}}_{G}=0\qquad \Rightarrow \qquad x_{G}=x_{G0}+v_{G0}t$

y la segunda es la de un oscilador armónico

${\ddot {x}}=-\omega ^{2}x\qquad \qquad \omega ={\sqrt {\frac {k(m_{1}+m_{2})}{m_{1}m_{2}}}}$

con solución

$x=c_{1}\cos(\omega t)+c_{2}\,\mathrm {sen} (\omega t)$

Los valores de las constantes salen de las condiciones iniciales. Para la posición del CM

$x_{G}(t=0)={\frac {m_{1}x_{10}+m_{2}x_{20}}{m_{1}+m_{2}}}={\frac {m_{2}\ell _{0}}{m_{1}+m_{2}}}\qquad \qquad {\dot {x}}_{G}(t=0)={\frac {m_{1}{\dot {x}}_{10}+m_{2}{\dot {x}}_{20}}{m_{1}+m_{2}}}={\frac {m_{2}v_{0}}{m_{1}+m_{2}}}$

lo que nos da, para todo instante

$x_{G}={\frac {m_{2}}{m_{1}+m_{2}}}(\ell _{0}+v_{0}t)$

Para la elongación del muelle

$x(t=0)=x_{20}-x_{10}-\ell _{0}=0\qquad \qquad {\dot {x}}(t=0)={\dot {x}}_{20}-{\dot {x}}_{10}=v_{0}$

siendo por tanto la elongación para todo instante

$x={\frac {v_{0}}{\omega }}\,\mathrm {sen} (\omega t)$

Conocidas las dos coordenadas obtenemos las posiciones de las dos masas

$x_{1}={\frac {m_{2}}{m_{1}+m_{2}}}(\ell _{0}+v_{0}t)-{\frac {m_{2}}{m_{1}+m_{2}}}\left(\ell _{0}+{\frac {v_{0}}{\omega }}\,\mathrm {sen} (\omega t)\right)={\frac {m_{2}}{m_{1}+m_{2}}}\left(v_{0}t-{\frac {v_{0}}{\omega }}\,\mathrm {sen} (\omega t)\right)$

 

$x_{2}={\frac {m_{2}}{m_{1}+m_{2}}}(\ell _{0}+v_{0}t)+{\frac {m_{1}}{m_{1}+m_{2}}}\left(\ell _{0}+{\frac {v_{0}}{\omega }}\,\mathrm {sen} (\omega t)\right)=\ell _{0}+{\frac {v_{0}}{\omega (m_{1}+m_{2})}}\left(m_{2}\omega t+m_{1}\,\mathrm {sen} (\omega t)\right)$

Constantes de movimiento

Empleando las nuevas coordenadas, vemos que x_G es cíclica, esto es, no aparece en la lagrangiana. Por tanto su momento conjugado es una constante de movimiento

$p_{G}=(m_{1}+m_{2}){\dot {x}}_{G}=m_{1}{\dot {x}}_{1}+m_{2}{\dot {x}}_{2}=\mathrm {cte.}$

Esta magnitud no es otra que la cantidad de movimiento del sistema.

La otra constante procede de que la lagrangiana no depende del tiempo. Como además la energía cinética es una función cuadrática de las velocidades, la cantidad conservada es la energía mecánica

$E={\frac {1}{2}}(m_{1}+m_{2}){\dot {x}}_{G}^{2}+{\frac {m_{1}m_{2}}{2(m_{1}+m_{2})}}{\dot {x}}^{2}+{\frac {1}{2}}kx^{2}={\frac {1}{2}}m_{1}{\dot {x}}_{1}^{2}+{\frac {1}{2}}m_{2}{\dot {x}}_{2}^{2}+{\frac {1}{2}}k(x_{2}-x_{1}-\ell _{0})^{2}$