Esfera sobre un plano inclinado con una cuerda horizontal, Febrero 2013 (G.I.C.)
Enunciado
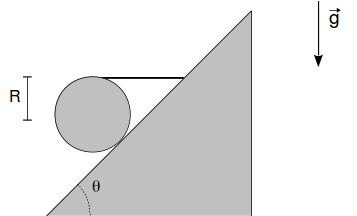
Una esfera uniforme de masa y radio se mantiene en reposo sobre un plano inclinado un ángulo mediante una cuerda horizontal, como se indica en la figura. El contacto entre la esfera y el plano es rugoso con coeficiente de rozamiento estático .
- Dibuja el diagrama de cuerpo libre de la esfera.
- Calcula la tensión de la cuerda, la fuerza de rozamiento y la reacción del plano sobre la esfera.
- Analiza los valores del ángulo para los cuales es posible el equilibrio.
Solución
Diagrama de cuerpo libre
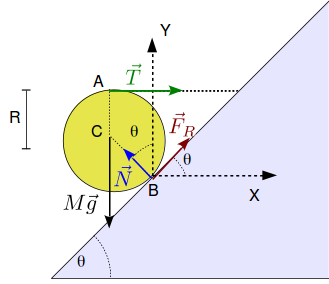
La figura de la derecha muestra las fuerzas que actúan sobre la esfera y su punto de aplicación. El peso se aplica en el centro de la esfera. La tensión de la cuerda es horizontal y se aplica en el punto . La reacción normal del plano y la fuerza de rozamiento entre el plano y la esfera se aplican en el punto .
Escogemos como ejes de coordenadas los indicados en la figura. En estos ejes las fuerzas se expresan como
Tensión de la cuerda, fuerza de rozamiento y reacción del plano
Las condiciones de equilibrio estático son que la suma de fuerzas y el momento resultante de las fuerzas respecto de un punto sean nulos. Aplicando que la suma de fuerzas es nula tenemos
Elegimos el punto para calcular el momento. De este modo el momento de la normal y el peso es cero. El momento de la fuerza ejercida por la cuerda es
Hemos usado el hecho de que los dos vectores son perpendiculares. El par de la fuerza de rozamiento es
El momento resultante ha de ser nulo. Entonces
Con esto tenemos tres ecuaciones para las incógnitas , y . Despejando obtenemos
Veamos un par de límites par verificar que el resultado es razonable. Si , tenemos que tanto como tienden a cero. En ese caso es la reacción normal del plano la que compensa al peso.
Si , todas las fuerzas tienden al valor . En esta situación, es la fuerza de rozamiento la que compensaría al peso, mientras que la fuerza de rozamiento lo haría con la fuerza ejercida por la cuerda.
Análisis del equilibrio
Para que la fuerza de rozamiento sea capaz de mantener la posición de equilibrio es necesario que se cumpla la condición
donde es el coeficiente de rozamiento estático. Eso impone una condición para el ángulo. Para que haya equilibrio debe ocurrir
Podemos calcular el valor del ángulo para el cual la expresión anterior es una igualdad. Usando que obtenemos una ecuación de segundo grado para .
La solución corresponde a la situación a la que la esfera está sobre una superficie horizontal. Podemos descartarla. La otra solución es
La condición de equilibrio puede escribirse
De aquí podemos deducir que hay un valor de para el cual siempre hay equilibrio. Si la expresión de la derecha es mayor o igual que 1, la condición de equilibrio se cumple siempre, pues el seno siempre es menor que 1. El valor es entonces




























