Ejemplos de movimiento rectílineo

Enunciado

Una partícula se mueve sobre el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX} según el movimiento dado por la siguientes expresiones. En todos los casos asumimos que el movimiento comienza en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0} .

1. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = A\,t} .
2. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = B\,(-1+t^2/T^2)} .
3. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = C\,(1-t/T)(4-t^2/T^2)} .
4. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = D\,\mathrm{sen}\,(2\pi t/T)} .
5. Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = D\,\left(1-e^{-t/T}\right)} .

Para cada caso, haz un dibujo aproximado de la gráfica que representa el movimiento. Determina en cada caso los instantes de tiempo en los que la partícula se encuentra en el origen, en la parte positiva y en la parte negativa del eje. Si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} se mide en metros y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t} en segundos, determina las unidades de las constantes que aparecen en las expresiones.

Solución

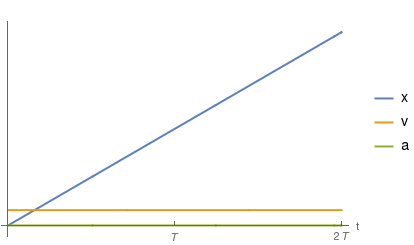
Caso 1

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = A\,t }

Las unidades de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} deben ser las adecuadas para hacer coherente dimensionalmente la expresión de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t)} . Como Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} se mide ne metros y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t} en segundos tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle [A] = m/s }

Esta curva es una línea recta que pasa por el origen y tiene pendiente Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} . Para que el punto esté en el origen debe ocurrir

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = At = 0 \Longrightarrow t=0 }

Sólo está en el origen en el instante inicial. El resto del tiempo la coordenada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} es positiva.

La velocidad es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t) = \dfrac{\mathrm{d}x}{\mathrm{d}t} = A. }

La partícula no se para nunca, pues Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t)} nunca es cero.

La aceleración es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a(t) = \dfrac{\mathrm{d}v}{\mathrm{d}t} = 0. }

El diferencial de posición es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}x = v\,\mathrm{d}t = A\,\mathrm{d}t. }

El diferencial de velocidad es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}v = a\,\mathrm{d}t = 0. }

La velocidad no cambia nunca.

Caso 2

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = B\,(-1+t^2/T^2)}

Las unidades de las constantes son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle [B]=m, \qquad \qquad [T]=s }

Esta curva es una parábola pues es una función cuadrática en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t} . Vamos a examinarla para poder bosquejar la gráfica

• En Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0} tenemos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(0)=-B} .

• Veamos para que instante se halla la partícula en el origen

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = 0 \Longrightarrow t=\pm T \Longrightarrow t = T }

Escogemos el valor positivo pues el movimiento ocurre en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t\geq 0} . Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t<T \to x(t)<0, \qquad\qquad t>T\to x(t)>0 }

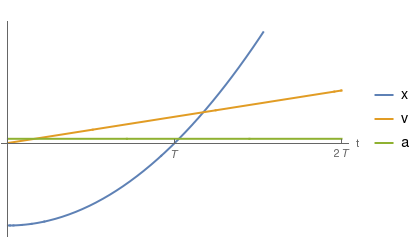
• Buscamos los máximos y mínimos. La derivada se anula en

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x'(t) = \dfrac{2B}{T^2}t=0 \Longrightarrow t=0 }

Es un mínimo pues

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left.x''(t)\right|_{t=0} = \dfrac{2B}{T} >0 }

La velocidad es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t) = \dfrac{\mathrm{d}x}{\mathrm{d}t} = 2B\dfrac{t}{T^2}. }

La velocidad sólo es cero en el instante inicial $t=0$.

La aceleración es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a(t) = \dfrac{\mathrm{d}v}{\mathrm{d}t} = \dfrac{2B}{T^2}. }

La aceleración es constante y nunca se anula.

El diferencial de posición es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}x = v\,\mathrm{d}t = 2B\dfrac{t}{T^2}\,\mathrm{d}t. }

El de velocidad es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}v = a\,\mathrm{d}t = \dfrac{2B}{T^2}\,\mathrm{d}t. }

Este movimiento es rectilíneo y uniformemente acelerado. La gráfica muestra las curvas correspondientes a la posición (una parábola), la velocidad (una línea recta) y la aceleración (una constante).

Caso 3

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = C(1-t/T)(4-t^2/T^2) }

Las unidades de las constantes son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle [C]=m, \qquad \qquad [T]=s }

Esta curva es un polinomio de grado 3. Vamos a examinarla para poder bosquejar la gráfica

• En Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0} tenemos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(0)=4C} .

• Veamos para que instante se halla la partícula en el origen

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = 0 \Longrightarrow t=\pm T, \pm 2T \Longrightarrow t = T, 2T }

Escogemos los valores positivos pues el movimiento ocurre en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t\geq 0} . Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} t<T \to x(t)>0 \\ T<t<2T\to x(t)<0\\ t>2T \to x(t)>0 \end{array} }

• Buscamos los máximos y mínimos para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t\geq0} . La derivada se anula en

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x'(t) = \dfrac{C}{T^3}(3t^2-2tT-4T^2) =0 \Longrightarrow t=1.54T }

Es un mínimo pues

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left.x''(t)\right|_{t=1.54T} =\left. \dfrac{A}{T^3}(6t-2T)\right|_{t=1.54T} = 7.21\dfrac{A}{T^3}>0 }

La velocidad de la partícula es la derivada respecto al tiempo de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t)}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t) = x'(t) = \left(\dfrac{\mathrm{d}x}{\mathrm{d}t}\right) = \dfrac{C}{T^3}(3t^2-2tT-4T^2) }

La partícula está en reposo cuando su derivada es cero

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t)==0 \Longrightarrow t = 1.54T. }

De las dos soluciones hemos escogido la que corresponde al intervalo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t\geq0} .

La aceleración es la derivada de la velocidad respecto del tiempo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a(t) = v'(t) = \left(\dfrac{\mathrm{d}v}{\mathrm{d}t}\right) = \dfrac{C}{T^3}(6t-2T) }

La aceleración es nula para

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a(t)==0 \Longrightarrow t = 0.33T. }

La figura de la derecha muestra las curvas correspondientes a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t)} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t)} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a(t)} .

El diferencial de posición es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}x = \left(\dfrac{\mathrm{d}x}{\mathrm{d}t}\right)\,\mathrm{d}x = v(t)\,\mathrm{d}x = \dfrac{C}{T^3}(3t^2-2tT-4T^2)\,\mathrm{d}t. }

Y el de velocidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}v = \left(\dfrac{\mathrm{d}v}{\mathrm{d}t}\right)\,\mathrm{d}x = a(t)\,\mathrm{d}x = \dfrac{C}{T^3}(6t-2T)\,\mathrm{d}t. }

Caso 4

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = D\,\mathrm{sen}\,(2\pi t/T)}

Esto es una sinusoide de período Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle T} . El argumento de las funciones trigonómetricas debe ser adimensional. Entonces las unidades de las constantes son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle [D] = m, \qquad [T]=s }

Buscamos los instantes en que la partícula está en el origen

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\,\left(\dfrac{2\pi}{T}t\right)=0 \to \dfrac{2\pi}{T}t = n\pi\quad (n=0,1,2,\ldots) \to t_n = n\dfrac{T}{2}\quad (n=0,1,2,\ldots) }

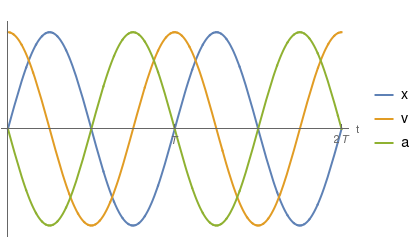
La posición empieza siendo positiva en el primer intervalo y luego cambia de signo a cada intervalo de tiempo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle T/2} .

La velocidad de la partícula es la derivada respecto al tiempo de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t)}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t) = x'(t) = \left(\dfrac{\mathrm{d}x}{\mathrm{d}t}\right) = \dfrac{2\pi A}{T}\cos\left(\dfrac{2\pi t}{T}\right) }

La partícula está en reposo cuando Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t)=0} , es decir

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos\left(\dfrac{2\pi}{T}t\right)=0 \to \dfrac{2\pi}{T}t = \left(n+\dfrac{1}{2}\right)\pi\quad (n=0,1,2,\ldots) \to t_n = \left(n+\dfrac{1}{2}\right)\dfrac{T}{2}\quad (n=0,1,2,\ldots) }

La aceleración es la derivada respecto al tiempo de la velocidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a(t) = v'(t) = \left(\dfrac{\mathrm{d}v}{\mathrm{d}t}\right) = -\dfrac{4\pi^2 A}{T^2}\,\mathrm{sen}\,\left(\dfrac{2\pi t}{T}\right) }

Se anula en los mismos instantes de tiempo que la posición, como se puede ver en la gráfica.

El diferencial de posición es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}x = v\,\mathrm{d}t = \dfrac{2\pi A}{T}\cos\left(\dfrac{2\pi t}{T}\right)\,\mathrm{d}t. }

Y el de velocidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}v = a\,\mathrm{d}t = -\dfrac{4\pi^2 A}{T^2}\,\mathrm{sen}\,\left(\dfrac{2\pi t}{T}\right) \mathrm{d}t. }

Caso 5

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t) = D\,\left(1-e^{-t/T}\right)}

Esta curva involucra una exponencial. El argumento de exponenciales y logaritmos debe ser adimensional. Entonces las unidades de las constantes son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle [D] = m, \qquad [T]=s }

• Veamos cuando está la partícula en el origen

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t)=0 \to e^{-t/T}=1 \to t=0 }

Sólo está en el origen en el instante inicial.

• Veamos los máximos y mínimos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x'(t) = \dfrac{D}{T}\,e^{-t/T} = 0 }

Eso no ocurre nunca, es decir la curva no tiene máximos ni mínimos. Ademas, es siempre creciente pues Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x'(t)>0} en todo instante.

• Pero también está acotada. Cuando Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t\to\infty} , se tiene

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle e^{-t/T}\to0} . Entonces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t)\leq D \qquad \forall t }

La velocidad de la partícula es la derivada respecto al tiempo de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t)}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t) = x'(t) = \left(\dfrac{\mathrm{d}x}{\mathrm{d}t}\right) = \dfrac{D}{T}\,e^{-t/T}. }

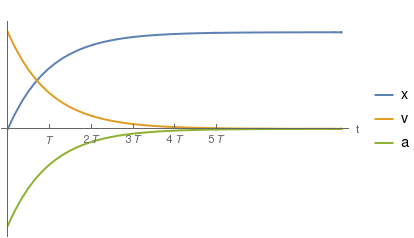
La partícula está en reposo cuando su derivada es cero.

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t)=0 \Longrightarrow t \to \infty }

La aceleración es la derivada de la velocidad respecto del tiempo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a(t) = v'(t) = \left(\dfrac{\mathrm{d}v}{\mathrm{d}t}\right) = -\dfrac{D}{T^2}\,e^{-t/T}. }

Es siempre negativa y sólo se anula en el infinito.

La figura de la derecha muestra las curvas correspondientes a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(t)} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v(t)} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a(t)} . Podemos ver de la figura que cuando Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=5T} el valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} es casi indistinguible del de la asíntota. La constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle T} da una idea de cuando tarda la función en alcanzar el valor asintótico, es decir, nos da la escala de tiempo típica del sistema.

El diferencial de posición es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}x = \left(\dfrac{\mathrm{d}x}{\mathrm{d}t}\right)\,\mathrm{d}x = v(t)\,\mathrm{d}x = \dfrac{D}{T}e^{-t/T}\,\mathrm{d}t. }

Y el de velocidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{d}v = \left(\dfrac{\mathrm{d}v}{\mathrm{d}t}\right)\,\mathrm{d}x = a(t)\,\mathrm{d}x = -\dfrac{D}{T^2}e^{-t/T}\,\mathrm{d}t. }