Ecuaciones de la dinámica del sólido rígido (CMR)

Introducción

Un sólido, como cualquier otro sistema de partículas está sometido a un conjunto de fuerzas. Las fuerzas sobre cada partícula pueden ser internas (debidas a otra partícula del mismo sólido) o externas (debidas a un agente externo, como la gravedad o un campo eléctrico aplicado).

Las fuerzas internas son importantes en cuanto a que son las que producen la propia existencia del sólido. Se trata de fuerzas cohesivas intensas que consiguen que cada átomo mantenga una posición aproximadamente fija respecto al resto de partículas del sólido.

Sin embargo, una vez admitida la aplicabilidad del modelo de sólido rígido, podemos ignorar la presencia de las fuerzas internas.

La razón es la siguiente: el movimiento de un sólido rígido posee 6 grados de libertad, que se pueden describir mediante las tres componentes de la velocidad lineal de un punto y las tres componentes de la velocidad angular del sólido. A su vez, estos dos vectores se relacionan directamente con la cantidad de movimiento y el momento angular del sólido.

Por tanto, para determinar las ecuaciones de movimiento del sólido nos basta con el teorema de la cantidad de movimiento y el teorema del momento angular. Para un sistema de partículas cualquiera (entre los que se incluye el sólido rígido), las ecuaciones de evolución de ${\vec {p}}$ y ${\vec {L}}_{O}$ dependen exclusivamente de las fuerzas externas aplicadas sobre el sistema, por lo que podemos restringirnos a ellas.

Suponemos entonces que sobre la partícula $m_{i}$ de un sólido actúa la fuerza externa ${\vec {F}}_{i}$. Estas fuerzas pueden ser debidas a que algún agente externo actúa sobre ellas o pueden ser fuerzas de reacción vincular (o una combinación de ambas). Así, en una articulación entre dos sólidos, cada uno de ellos experimenta un conjunto de fuerzas de reacción vincular que los obligan a moverse como corresponde al par cinemático correspondiente y no de otra forma.

Campo de velocidades del sólido

Según el teorema de Chasles, la velocidad de cualquier punto de un sólido puede hallarse conocida la velocidad de un punto de referencia, O, y la velocidad angular del sólido

${\vec {v}}_{21}^{P}={\vec {v}}_{21}^{O}+{\vec {\omega }}_{21}\times {\overrightarrow {OP}}$

con el caso particular

${\vec {v}}_{21}^{P}={\vec {v}}_{21}^{G}+{\vec {\omega }}_{21}\times {\overrightarrow {GP}}$

siendo G el centro de masas del sólido.

Movimiento del centro de masas

Para determinar el movimiento del centro de masas nos basta con aplicar que para un sistema de partículas

${\vec {p}}=M{\vec {v}}_{21}^{G}$

y, derivando aquí respecto al tiempo,

${\vec {a}}_{21}^{G}={\frac {1}{M}}{\vec {F}}$

siendo ${\vec {F}}$ la resultante de todas las fuerzas externas aplicadas sobre el sólido, independientemente de sobre qué partícula se apliquen.

Según esto, basta con sumar vectorialmente las diferentes fuerzas externas aplicadas para determinar la aceleración del CM, el cual se moverá como una partícula cuya masa sea la total del sólido.

En el caso particular del peso, la resultante es

${\vec {F}}=\int _{M}{\vec {g}}\,\mathrm {d} m={\vec {g}}\,\int _{M}\mathrm {d} m=M{\vec {g}}$

Es decir, la resultante del peso de todo el sólido equivale al peso de una sola partícula cuya masa sea la total del sólido. Esta ecuación, junto con la anterior, nos dice que si un objeto es lanzado y se encuentra sometido exclusivamente a su peso, su centro de masas describe una parábola.

Este resultado no quiere decir que el sólido efectúe un movimiento de traslación con la velocidad del CM, sino que, en general, el sólido describirá un movimiento de rotación en torno al centro de masas. Para determinar la evolución de la velocidad angular con la que rota debemos recurrir a la ecuación para el momento angular.

Movimiento alrededor del centro de masas

De acuerdo con las propiedades de un sistema de partículas, el momento angular de un sólido respecto a un punto O equivale a

${\vec {L}}_{O}=M{\overrightarrow {OG}}\times {\vec {v}}_{21}^{G}+{\vec {L}}_{G}$

con ${\vec {L}}_{G}$ el momento angular correspondiente al movimiento respecto al CM (calculado con las velocidades absolutas o las relativas a G; para el centro de masas ambos momentos cinéticos son coincidentes). En el caso de un sólido simétrico respecto al eje de giro, esta expresión se reduce a

${\vec {L}}_{O}=M{\overrightarrow {OG}}\times {\vec {v}}_{21}^{G}+I{\vec {\omega }}_{21}$

En el caso general será necesario usar el tensor de inercia.

${\vec {L}}_{O}=M{\overrightarrow {OG}}\times {\vec {v}}_{21}^{G}+{\overline {\overline {I}}}\cdot {\vec {\omega }}_{21}$

Su derivada respecto al tiempo nos da la ecuación de movimiento para la rotación del sólido.

El teorema del momento angular para un sistema de partículas establece que, dado un punto fijo O,

${\frac {\mathrm {d} {\vec {L}}_{O}}{\mathrm {d} t}}={\vec {M}}_{O}$

siendo ${\vec {M}}_{O}$ el momento resultante respecto al punto O de las fuerzas aplicadas

${\vec {M}}_{O}=\sum _{i}{\overrightarrow {OP}}_{i}\times {\vec {F}}_{i}$

Este teorema también es aplicable al centro de masas, aunque se trate de un punto móvil, es decir

${\frac {\mathrm {d} {\vec {L}}_{G}}{\mathrm {d} t}}={\vec {M}}_{G}\qquad \qquad {\vec {M}}_{G}=\sum _{i}{\overrightarrow {GP}}_{i}\times {\vec {F}}_{i}$

Por tanto, para determinar la rotación del sólido en torno al CM nos basta con calcular la resultante de las momentos respecto al CM de las diferentes fuerzas aplicadas sobre el sólido.

En el caso del centro de masas, esta derivada temporal es igual a

${\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\overline {\overline {I}}}\cdot {\vec {\omega }}_{21}\right)={\frac {\mathrm {d} {\overline {\overline {I}}}}{\mathrm {d} t}}\cdot {\vec {\omega }}_{21}+{\overline {\overline {I}}}\cdot {\frac {\mathrm {d} {\vec {\omega }}_{21}}{\mathrm {d} t}}$

A diferencia de la ecuación de la cantidad de movimiento, en la que la masa es una constante, el momento de inercia es una función del tiempo, incluso en casos de sólidos simétricos. La razón es que el sólido puede estar cambiando en el tiempo su posición relativa respecto al eje, por lo que en cada instante I va a representar una magnitud diferente.

Despejando, queda la ecuación para la aceleración angular

${\overline {\overline {I}}}\cdot {\vec {\alpha }}_{21}=-{\frac {\mathrm {d} {\overline {\overline {I}}}}{\mathrm {d} t}}\cdot {\vec {\omega }}_{21}+{\vec {M}}_{G}$

El tensor de inercia puede hacerse constante si se eligen unos ejes ligados al sólido, pero en ese caso es preciso tener en cuenta el movimiento de los ejes. Cuando se hace de esta forma se obtienen las ecuaciones de Euler.

Suponiendo un sólido simétrico, el momento de inercia es constante en los siguientes casos particulares de interés:

• Rotación en torno a un eje fijo (p.ej. un rotor, o un péndulo que oscila en torno a un anclaje fijo).
• El momento de inercia es independiente del eje que se elija, siempre que pase por el CM del sólido (p.ej., para una esfera, pero también para un sólido cúbico).

En esos casos, la ecuación se reduce a

${\vec {M}}_{G}=I{\vec {\alpha }}_{21}$

la aceleración angular. Esta ecuación es el análogo para rotación de la segunda ley de Newton.

Energía

Energía cinética

Tal como se ve al estudiar los sistemas de partículas, para la energía cinética de un sistema se cumple

${\frac {\mathrm {d} K}{\mathrm {d} t}}=\sum _{i}{\vec {v}}_{21}^{P_{i}}\cdot {\vec {F}}_{i}$

donde ${\vec {F}}_{i}$ es la resultante de las fuerzas sobre la partícula i, incluyendo tanto las fuerzas externas como las internas entre partículas del propio sistema.

Ahora bien, si consideramos la contribución de las fuerzas entre un par de partículas A y B del sólido, nos quedan términos de la forma

${\vec {v}}_{21}^{A}\cdot {\vec {F}}_{B\to A}+{\vec {v}}_{21}^{B}\cdot {\vec {F}}_{A\to B}$

Aplicando aquí la tercera ley de Newton

${\vec {F}}_{B\to A}=-{\vec {F}}_{A\to B}$

esta contribución se reduce a

${\vec {v}}_{21}^{A}\cdot {\vec {F}}_{B\to A}+{\vec {v}}_{21}^{B}\cdot {\vec {F}}_{A\to B}=\left({\vec {v}}_{21}^{B}-{\vec {v}}_{21}^{A}\right)\cdot {\vec {F}}_{A\to B}$

En el caso de un sólido rígido se cumple

${\vec {v}}_{21}^{B}-{\vec {v}}_{21}^{A}={\vec {\omega }}_{21}\times {\overrightarrow {AB}}$

y por tanto

${\vec {v}}_{21}^{A}\cdot {\vec {F}}_{B\to A}+{\vec {v}}_{21}^{B}\cdot {\vec {F}}_{A\to B}=\left({\vec {\omega }}_{21}\times {\overrightarrow {AB}}\right)\cdot {\vec {F}}_{A\to B}={\vec {\omega }}_{21}\cdot \left({\overrightarrow {AB}}\times {\vec {F}}_{A\to B}\right)$

Una fuerza newtoniana entre dos partículas va en la dirección de la recta que las une. Por tanto, el último término es nulo.

Esto implica que la contribución de todas las fuerzas internas se anula y la potencia sobre un sólido se reduce a

${\frac {\mathrm {d} K}{\mathrm {d} t}}=\sum _{i}{\vec {v}}_{21}^{P_{i}}\cdot {\vec {F}}_{i\mathrm {ext} }$

es decir, solo necesitamos hallar la potencia desarrollada por las fuerzas externas. En particular, si el punto de aplicación tiene velocidad nula (caso de la rodadura sin deslizamiento, por ejemplo), la fuerza no introduce energía en el sistema.

Aplicando aquí la expresión del campo de velocidades del sólido

${\vec {v}}_{21}^{P_{i}}={\vec {v}}_{21}^{O}+{\vec {\omega }}_{21}\times {\overrightarrow {OP}}_{i}$

queda, para la potencia total

${\frac {\mathrm {d} K}{\mathrm {d} t}}=P=\sum _{i}\left({\vec {v}}_{21}^{O}+{\vec {\omega }}_{21}\times {\overrightarrow {OP}}_{i}\right)\cdot {\vec {F}}_{i\mathrm {ext} }$

Agrupando términos

${\frac {\mathrm {d} K}{\mathrm {d} t}}=P={\vec {v}}_{21}^{O}\cdot \left(\sum _{i}{\vec {F}}_{i\mathrm {ext} }\right)+{\vec {\omega }}_{21}\cdot \left(\sum _{i}{\overrightarrow {OP}}_{i}\times {\vec {F}}_{i}\right)={\vec {v}}_{21}^{O}\cdot {\vec {F}}+{\vec {\omega }}_{21}\cdot {\vec {M}}_{O}$

En esta expresión, O es cualquier punto fijo, pero también puede ser el centro de masas del sólido.

Equivalentemente, esto nos dice que el trabajo diferencial realizado sobre un sólido por un sistema de fuerzas externas es igual a

$\delta W=\mathrm {d} K=({\vec {v}}_{21}^{G}\mathrm {d} t)\cdot {\vec {F}}+({\vec {\omega }}_{21}\mathrm {d} t)\cdot {\vec {M}}_{G}={\vec {F}}\cdot \mathrm {d} {\vec {r}}_{G}+{\vec {M}}_{G}\cdot {\vec {\omega }}\,\mathrm {d} t$

El producto ${\vec {\omega }}\,\mathrm {d} t$ es igual el ángulo girado en un diferencial de tiempo multiplicado por la dirección del eje de giro

${\vec {\omega }}_{21}\,\mathrm {d} t=\mathrm {d} \theta \,{\vec {u}}$

Esto nos da el trabajo diferencial

$\delta W={\vec {F}}\cdot \mathrm {d} {\vec {r}}_{G}+M_{\omega }\,\mathrm {d} \theta$

que nos dice que el trabajo para cambiar el estado de rotación es igual a la componente del momento en la dirección del eje de giro (la única que realiza trabajo) multiplicada por el ángulo girado. Es de nuevo una analogía entre traslación y rotación.

Energía potencial

Operando igualmente, obtenemos para la energía potencial

${\frac {\mathrm {d} U}{\mathrm {d} t}}=-\sum _{i}{\vec {v}}_{21}^{P_{i}}\cdot {\vec {F}}_{i\mathrm {ext} ,c}$

donde el subíndice c se refiere a que solo aparecen las fuerzas conservativas.

Energía mecánica

Considerando que el sólido está sometido a fuerzas conservativas, fuerzas de reacción que no realizan trabajo y fuerzas no conservativas, podemos sumar las dos expresiones anteriores y escribir la ley para la evolución de la energía mecánica

$E=K+U=K_{T}+K_{R}+U\,$

en la forma

${\frac {\mathrm {d} E}{\mathrm {d} t}}=\sum _{i}{\vec {v}}_{21}^{P_{i}}\cdot {\vec {F}}_{i\mathrm {ext} ,nc}$

donde la suma solo incluye las fuerzas externas no conservativas.

De aquí se deduce que si sobre un sólido solo actúan fuerzas externas conservativas, su energía mecánica se conserva. En ese caso, es importante recordar que la energía cinética incluye tanto energía de traslación como de rotación y que la energía se puede repartir de múltiples formas entre ambos tipos de energía cinética.

En el caso de que el sólido esté sometido exclusivamente al peso (y a fuerzas de reacción que no realizan trabajo), la conservación de la energía mecánica para un sólido simétrico queda

${\frac {1}{2}}M|{\vec {v}}_{21}^{G}|^{2}+{\frac {1}{2}}I|{\vec {\omega }}|^{2}+Mgz_{G}=\mathrm {cte}$

Esta ley nos dice que cuando un cuerpo desciende rodando por un plano inclinado, su centro se mueve más lentamente que si se deslizara por él, ya que parte de la energía potencial se trasforma en energía cinética de rotación, con lo que el aumento de energía cinética de traslación es menor.

Fuerzas y momentos de reacción

Cuando tenemos un contacto entre dos sólidos y entre ellos se forma un par cinemático, los grados de libertad del movimiento relativo se ven reducidos. O bien uno de los sólidos no puede moverse en una dirección o en otra, o no puede girar, o no puede moverse de ninguna de las formas…

Estas restricciones sobre el movimiento se producen porque uno de los sólidos ejerce fuerzas sobre el otro (y viceversa, de acuerdo con la tercera ley de Newton). Estas fuerzas son de contacto y en principio difíciles de determinar individualmente pues para saber la distribución de fuerzas punto a punto es preciso salirse del modelo de sólido rígido. Lo que si se puede determinar es la resultante de las fuerzas de reacción, ${\vec {F}}_{R}$ y el momento resultante de estas fuerzas de reacción respecto al punto O de contacto, que denotaremos con la letra ${\vec {M}}_{RO}$.

Según esto, podemos sustituir cada vínculo por una combinación de fuerza y par $\{{\vec {F}}_{R},{\vec {M}}_{R}\}$ cuyo efecto dinámico es el mismo del vínculo al que sustituyen. La fuerza y el par se suponen aplicados en el punto de contacto entre los sólidos. En principio, cada uno de ellos puede tener una dirección arbitraria

${\vec {F}}_{R}=F_{x}{\vec {\imath }}+F_{y}{\vec {\jmath }}+F_{z}{\vec {k}}\qquad \qquad {\vec {M}}_{RO}=M_{x}{\vec {\imath }}+M_{y}{\vec {\jmath }}+M_{z}{\vec {k}}$

pero si el vínculo permite un determinado desplazamiento libre, por ejemplo, en la dirección del eje Z, quiere decir que no se está ejerciendo ninguna fuerza de reacción en dicha dirección por lo que $F_{z}=0$. Por ello, para cada par cinemático, las componentes nulas son las correspondientes a los grados de libertad disponibles. Así, para los casos más usuales tenemos las fuerzas y pares de reacción siguientes:

Par cilíndrico (corredera cilíndrica)

El sólido 2 está obligado a girar en torno a un cierto eje, sobre el cual puede haber una cierta velocidad de deslizamiento. El vínculo se produce mediante una fuerza perpendicular a la dirección de deslizamiento y un momento que impide girar en una dirección diferente a la del eje.

${\vec {F}}_{R}=F_{x}{\vec {\imath }}+F_{y}{\vec {\jmath }}\qquad \qquad {\vec {M}}_{RO}=M_{x}{\vec {\imath }}+M_{y}{\vec {\jmath }}$

O equivalentemente, no hay fuerza ni par en los sentidos de movimiento admisibles

$F_{z}=0\qquad \qquad M_{z}=0$

Par helicoidal (tornillo)

Como en el anterior, el sólido 2 gira en torno a un eje dado, sobre el cual se desliza, pero la velocidad de deslizamiento no es arbitraria, sino que está condicionada por el paso de rosca, $b$, que es la distancia que avanza cuando gira una vuelta completa. Como en el caso anterior, existe un para y una fuerza con componentes transversales, pero cuyas componentes longitudinales no son nulas, sino que están relacionadas por el hecho de que fuerzan al movimiento helicoidal

$F_{z}b+2\pi M_{z}=0\,$

Par de revolución (bisagra)

De nuevo el eje de giro está fijado, pero ahora la velocidad de deslizamiento es nula. La fuerza de reacción pueden tener cualquier valor, mientras que el par de reacción no tiene componente en la dirección en que el giro es libre

$M_{z}=0\,$

Par prismático (corredera rectangular)

El sólido 2 puede deslizarse a lo largo de un cierto eje, pero no puede girar en torno a él (un único grado de libertad relativa). En este caso el par puede ir en cualquier dirección, pues se impide cualquier giro, mientras que la fuerza de reacción no tiene componente en la dirección en que se permite el deslizamiento

$F_{z}=0\,$

Par esférico (rótula o articulación)

El punto A (centro de la rótula) es un punto fijo en el movimiento relativo de los dos sólidos. El sólido 2 puede girar libremente (pero no trasladarse) respecto al 1. Por ello la fuerza de reacción puede tener cualquier dirección, mientras que el par de reacción es nulo, ya que todos los giros son posibles

${\vec {M}}_{RO}={\vec {0}}$

Par rígido (empotramiento, voladizo o cantilever)

Los dos sólidos forman en realidad uno solo, ya que en el punto de contacto la unión es rígida. En este caso puede haber una fuerza de reacción en cualquier dirección y par en cualquier dirección, no siendo nula ninguna de sus componentes.

Como en el caso de los vínculos sobre una partícula, los vínculos sobre sólidos pueden ser bilaterales o unilaterales. En el primer caso, se oponen a un desplazamiento o a una rotación en los dos sentidos, por lo que la ligadura se puede expresar como una igualdad y la componente correspondiente de la fuerza o del par puede tener cualquier signo. En el caso unilateral, se oponen a un desplazamiento o rotación en un sentido pero no en el opuesto, por lo que se expresan como desigualdades y la componente de la fuerza o el par puede tener un signo pero no el opuesto.

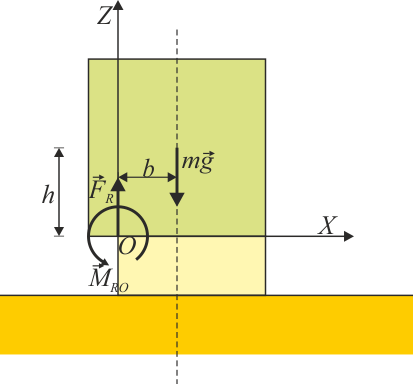
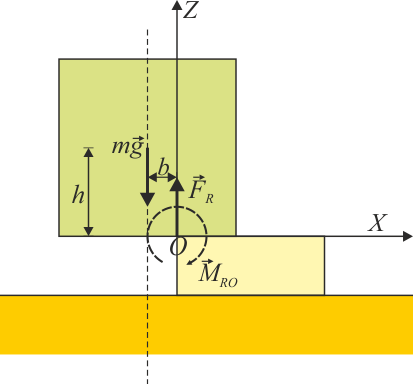
Como ejemplo de vínculo unilateral tenemos el del vuelco. Imaginemos una caja apoyada en una base inferior de anchura $B$. La caja ejerce una fuerza sobre la base, que es respondida con una reacción hacia arriba. En realidad, es una infinitud de reacciones distribuidas sobre toda la superficie de contacto.

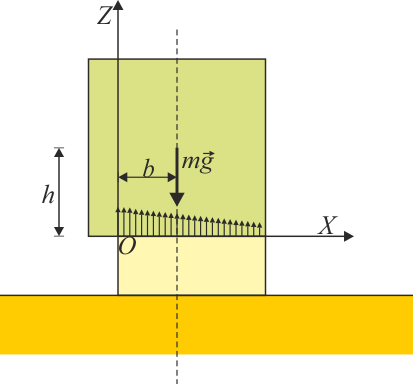
Si hallamos la resultante de las fuerzas y el momento resultante respecto de un punto del borde de la base (que tomamos como $x=0$, con la base en $x>0$), obtenemos ${\vec {F}}_{R}$ y ${\vec {M}}_{RO}$. Ahora bien, la reacción del suelo solo impide que la pila gire hacia el interior, pero no puede impedir que gire hacia el exterior y vuelque. Por ejemplo, supongamos que el centro de masas de la caja se encuentra a una distancia $b$ del borde de la base. La ecuaciones de equilibrio del bloque nos dan

${\vec {F}}-Mg{\vec {k}}={\vec {0}}\qquad \qquad {\vec {M}}_{RO}+(b{\vec {\imath }}+h{\vec {k}})\times (-Mg{\vec {k}})={\vec {0}}$

con lo que para que haya equilibrio la fuerza y el par de reacción deben valer

${\vec {F}}_{R}=Mg{\vec {k}}\qquad \qquad {\vec {M}}_{RO}=-Mgb{\vec {\jmath }}$

La primera ecuación se cumple sin problemas, pero la segunda no siempre es posible. Si $b<0$, implicaría un par de reacción que tiende a girar al bloque hacia la izquierda, lo cual es imposible. Dicho de otra forma, si hallamos la resultante de los momentos de las fuerzas de reacción punto a punto, siempre nos resultará un momento en sentido contrario. En ese caso la reacción no retiene a la caja y esta vuelca. La regla básica para que un objeto no vuelque es que la vertical del CM pase por el interior del perímetro de la base. Si se encuentra en el exterior se produce vuelco.