Dos rodillos unidos por un resorte (CMR)

Enunciado

Se tiene un sistema de dos rodillos (“2” y “3”) de la misma masa m y el mismo radio R, situados sobre una superficie horizontal (sólido 1), sobre la que pueden rodar sin deslizar. Los dos rodillos no son idénticos. El “2” es un cilindro macizo homogéneo (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \gamma=1/2} ), mientras que el “3” tiene su masa concentrada en la superficie cilíndrica (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \gamma=1} ). Los dos rodillos están conectados por un resorte de constante k y longitud natural Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ell_0} . Todo el sistema está sometido a la acción del peso.

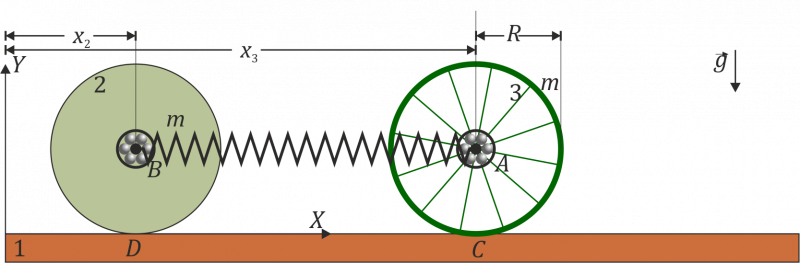
Estando en reposo en una posición de equilibrio, se sujeta el cilindro 2 y se desplaza el 3 una cierta distancia A, manteniéndolos en reposo. Entonces se sueltan los dos.

1. Halle la lagrangiana de este sistema, empleando como coordenadas generalizadas las posiciones Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_2} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_3} de las centros de los rodillos, medidas respecto a un sistema fijo.
2. Halle las ecuaciones de movimiento para las posiciones de los centros de los rodillos, esto es, halle Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot{x}_2} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot{x}_3} en función de las posiciones Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_2} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_3} .

Si en lugar de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_2} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_3} se emplean como coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_2} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x} , definida x como la longitud del resorte menos su longitud en el equilibrio

3. ¿Cómo queda la lagrangiana en función de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_2} y $x$?
4. ¿Y las ecuaciones de movimiento para estas coordenadas?
5. ¿Cuál es la frecuencia de oscilación del resorte?
6. ¿Y la posición de cada masa como función del tiempo?
7. ¿Qué constantes de movimiento existen en este problema?

Lagrangiana

Para cada rodillo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T=\frac{1}{2}m|\vec{v}_G|^2+\frac{1}{2}I|\vec{\omega}|^2=\frac{1}{2}m\dot{x}^2+\frac{1}{2}(\gamma m R^2)\left(-\frac{\dot{x}}{R}\right)^2=\frac{1}{2}(1+\gamma)m\dot{x}^2}

por lo que la energía cinética total es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T=\frac{3}{4}m\dot{x}_2^2+m\dot{x}^2_3}

La energía potencial es la de un resorte

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle U=\frac{1}{2}k(x_3-x_2-\ell_0)^2}

y la lagrangiana

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathcal{L}=\frac{m}{4}(3\dot{x}_2^2+4\dot{x}_3^2)-\frac{k}{2}(x_3-x_2-\ell_0)^2}

Ecuaciones de movimiento

Aplicando las ecuaciones de Lagrange

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial \dot{q}_k}\right)-\frac{\partial\mathcal{L}}{\partial {q}_k}=0}

queda

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} \dfrac{3}{2}m\ddot{x}_2-k(x_3-x_2-\ell_0)&=&0 \\&& \\ 2m\ddot{x}_3+k(x_3-x_2-\ell_0)&=&0 \end{array}}

y, despejando,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} \ddot{x}_2&=&\dfrac{2k}{3m}(x_3-x_2-\ell_0) \\ && \\ \ddot{x}_3&=&-\dfrac{k}{2m}(x_3-x_2-\ell_0) \end{array}}

Nueva lagrangiana

Con el cambio de variable

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\begin{array}{rcl}x_2&=&x_2 \\ x_3&=&x_2+\ell_0+x\end{array}\right.\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}\dot{x}_2&=&\dot{x}_2 \\ \dot{x}_3&=&\dot{x}_2+\dot{x}\end{array}\right.}

queda

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathcal{L}=\frac{m}{4}(3\dot{x}_2^2+4(\dot{x}_2+\dot{x})^2)-\frac{k}{2}x^2}

Nuevas ecuaciones de movimiento

Aplicando de nuevo las ecuaciones de Lagrange

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} \dfrac{1}{2}m(7\ddot{x}_2+4\ddot{x})&=&0 \\ && \\ 2m(\ddot{x}_2+\ddot{x})+kx&=&0 \end{array}}

Resolviendo el sistema de ecuaciones para las aceleraciones

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} \ddot{x}_2&=&\dfrac{2k}{3m}x \\ && \\ \ddot{x}&=&-\dfrac{7k}{6m}x \end{array}}

Frecuencia de oscilación

La ecuación para x es la de un oscilador armónico de frecuencia

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega=\sqrt{\frac{7k}{6m}}}

Posiciones de las masas

Las posiciones iniciales son, del enunciado,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_{20}=0\qquad\qquad x_0=A}

por lo que la solucín para la elongación del muelle es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x=A\cos(\omega t)\,}

y de aquí sale para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_2}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot{x}_2=\frac{2k}{3m}A\cos(\omega t)}

Integrando dos veces y aplicando la condición inicial

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x=\frac{4A}{7}(1-\cos(\omega t))}

Constantes de movimiento

En este sistema tenemos dos constantes de movimiento.

• El momento conjugado a la variable Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle x_2} que es cíclica

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle p_2=\frac{\partial\mathcal{L}}{\partial \dot{x}_2}=\frac{7}{2}m\dot{x}_2+2m\dot{x}}

Esta cantidad es similar a la cantidad de movimiento del sistema, pero no lo es.

• La hamiltoniana, pues la lagrangiana no depende del tiempo. En este caso, la hamiltoniana coincide con la energía mecánica

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \mathcal{H}=\frac{m}{4}(3\dot{x}_2^2+4(\dot{x}_2+\dot{x})^2)+\frac{k}{2}x^2=\frac{m}{4}(3\dot{x}_2^2+4\dot{x}_3^2)+\frac{k}{2}(x_3-x_2-\ell_0)^2}