Dos partículas conectadas por un muelle, Enero 2017 (G.I.C.)

Enunciado

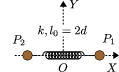
Dos partículas con la misma masa $m$ están unidas por un muelle de constante elástica $k$ y longitud natural $l_{0}=2d$. Debido a una perturbación externa, las dos masas empiezan a oscilar. Después de la perturbación, cada masa está sometida únicamente a la acción del muelle. Los ejes $X$ e $Y$ están indicados en la figura. El origen de coordenadas está en el punto medio entre las dos masas. Suponemos que el movimiento es rectilíneo sobre el eje $X$.

1. Fuerza sobre las partículas
2. Encuentra la frecuencia natural de las oscilaciones
3. Esta configuración puede modelar una molécula de hidrógeno (H2) o de Deuterio (D2), usando la misma constante elástica y la misma longitud natural para las dos. La frecuencia vibracional de la molécula de hidrógeno es $f_{0}=1.30\times 10^{14}\,\mathrm {Hz}$. Sabiendo que la masa de la molécula de deuterio es el doble de la masa de la molécula de hidrógeno, ¿cuál es la frecuencia de vibración de la molécula de deuterio, aproximadamente?

Solución

Fuerza sobre la masas

Sobre cada masa sólo ejerce fuerza el muelle. Para la masa $m_{1}$, la de la derecha, tenemos

${\vec {F}}_{1}=-k(l-l_{0})\,{\vec {u}}_{2\to 1}.$

Aquí, $l$ es la elongación del muelle, $l_{0}$ su longitud natural y ${\vec {u}}_{2\to 1}$ un vector unitario que vaya desde el extremo izquierdo del muelle hacia la masa $m_{1}$. Del dibujo vemos

${\vec {u}}_{2\to 1}={\vec {\imath }}.$

La longitud natural es $l_{0}=2d$. Para la elongación tenemos

$l=x_{1}-x_{2},$

donde $x_{1}$ y $m_{2}$ son las coordenadas de las partículas. La fuerza sobre la partícula 1 es

${\vec {F}}_{1}=-k(x_{1}-x_{2}-2d)\,{\vec {\imath }}.$

Hay que tener en cuenta que $x_{2}$ es la coordenada de la partícula 2, es decir, que tiene signo. Si la partícula 2 está a la izquierda del origen es negativa. Podemos hacer una prueba. Por ejemplo, si$x_{1}=d$ y $x_{2}=-d$, el muelle está relajado, pues la distancia entre las masas es igual a la longitud natural. Entonces la fuerza debería ser cero, y eso es lo que nos da la expresión.

La fuerza sobre la partícula 2 es

${\vec {F}}_{2}=-{\vec {F}}_{1}=k(x_{1}-x_{2}-2d)\,{\vec {\imath }}.$

Frecuencia natural de oscilación

La Segunda Ley de Newton aplicada a la masa 1 es

$m{\vec {a}}_{1}={\vec {F}}_{1}\Longrightarrow m{\ddot {x}}_{1}=-k(x_{1}-x_{2}-2d)$

Por simetría, como las dos masas son iguales se cumple

$x_{2}=-x_{1}.$

Es decir, el centro de masas coincide siempre con el punto medio entre las masas. Entonces la Segunda Ley para la masa 1 queda

$m{\ddot {x}}_{1}=-k(2x_{1}-2d)\Longrightarrow {\ddot {x}}_{1}=-{\dfrac {2k}{m}}x_{1}+{\dfrac {2kd}{m}}.$

Esta es la ecuación diferencial de movimiento de un oscilador armónico de frecuencia

$\omega ={\sqrt {\dfrac {2k}{m}}}$

La frecuencia natural es

$f={\dfrac {2\pi }{\omega }}={\sqrt {\dfrac {k}{2\pi ^{2}m}}}.$

Frecuencia de oscilación del deuterio

Lo que cambia entre las moléculas de hidrógeno y deuterio es la masa de los átomos. El cociente entre las frecuencias es

${\dfrac {f_{D}}{f_{H}}}={\dfrac {\sqrt {k/2\pi ^{2}m_{D}}}{\sqrt {k/2\pi ^{2}m_{H}}}}={\sqrt {\dfrac {m_{H}}{m_{D}}}}$

Por tanto

$f_{D}=f_{H}\,{\sqrt {\dfrac {m_{H}}{m_{D}}}}={\dfrac {f_{H}}{\sqrt {2}}}=9.19\times 10^{13}\,\mathrm {Hz} .$

Errores comunes detectados en la corrección

1. La coordenada $x_{2}$ tiene signo, como se ha indicado en la corrección.
2. EN FÍSICA NO VALE APLICAR CONJUROS MÁGICOS. Mucha gente ha visto un muelle y ha aplicado el conjuro

$\mathrm {muelle} \to \omega ={\sqrt {k/m}}.$

Eso es cierto cuando se tiene una masa conectada a un muelle con el otro extremo fijo. Pero este problema es distinto. Como hemos visto varias veces en clase, hay que analizar las fuerzas que actúan sobre las partículas, aplicar la Segunda Ley de Newton y obtener así la ecuación de movimiento. La magia es fácil de memorizar y aplicar. El único problema es que no funciona.