Enunciado
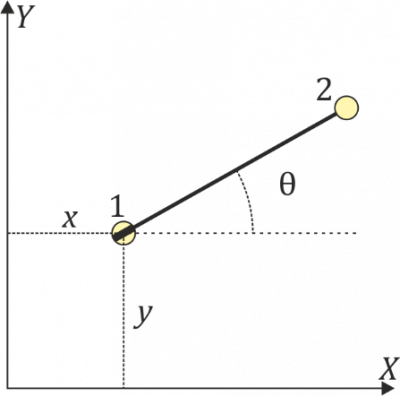
Dos masas iguales m están unidas por una varilla rígida ideal de longitud b. La varilla reposa sobre un plano horizontal. una de masas (la “2) puede deslizar sin rozamiento sobre el plano, pero la “1” está montada sobre una cuchilla que la obliga a desplazarse solo en la dirección paralela a la propia varilla
- ¿Qué vínculos ligan las posiciones y velocidades de las partículas?
- ¿Hacia dónde van dirigidas las fuerzas de reacción vincular?
- Escriba el sistema de ecuaciones de movimiento y de vínculos para este sistema empleando como variables las coordenadas cartesianas de la masa 1 y el ángulo que la varilla forma con el eje OX. Sugerencia: emplee tanto el sistema de referencia fijo “1” como el “2” ligado a la varilla.
- Introduciendo las variables adecuadas, reduzca este problema a un sistema de ecuaciones de primer orden.
Vínculos
Si identificamos la posición de cada partícula en el plano por sus coordenadas cartesianas, los vínculos sobre el sistema son tales que:
- La distancia entre las partículas es constante
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle |\overrightarrow{AB}|=b\qquad\Rightarrow\qquad(x_B-x_A)^2+(y_B-y_A)^2 = b^2\,}
- La velocidad de la partícula 1 es paralela al vector de posición relativa
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_A\times\overrightarrow{AB}=\vec{0}\qquad\Rightarrow\qquad (x_B-x_A)\dot{y}_A-(y_B-y_A)\dot{x}_A=0}
- Este vínculo no puede integrarse para dar un vínculo geométrico. No se puede integrar porque aparecen las derivadas de las coordenadas de la partícula 1 multiplicadas por las coordenadas de la partícula 2, que no dependen de la 1. Por ello no se puede escribir como la derivada de una sola función.
Si usamos como coordenadas las indicadas en el enunciado
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_A = x\qquad\qquad y_A = y\qquad\qquad x_B=x+bC\qquad\qquad y_B=y+bS}
(con C y S representando al coseno y el seno de θ), el primer vínculo se vuelve trivial
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle b=\mathrm{cte.}\,}
y el segundo se escribe
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -S\dot{x}+C\dot{y}=0}
Fuerzas de reacción
Asociadas a cada vínculo se producen fuerzas de reacción vincular.
- La partícula 1 se ve sometida a una fuerza por cada vínculo. Para el primero, la fuerza va en la dirección de la varilla.
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_{T1}=F_T(C\vec{\imath}+S\vec{\jmath})}
- Para el segundo, es perpendicular a la dirección de movimiento posible y por tanto, perpendicular a la varilla
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_{n1}=F_n(-S\vec{\imath}+C\vec{\jmath})}
- Sobre la segunda partícula solo actúa la tensión de la varilla, en sentido opuesto a la que actúa sobre la 1.
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_{T2}=-F_T(C\vec{\imath}+S\vec{\jmath})}
Ecuaciones de movimiento
Si separamos por componentes, las ecuaciones de movimiento son
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} m\ddot{x}_1 & = & F_TC-F_nS\\ m\ddot{y}_1 & = & F_TS+F_nC\\ m\ddot{x}_2 & = & -F_TC\\ m\ddot{y}_2 & = & -F_TS \end{array}}
En términos de las coordenadas sugeridas, derivamos dos veces Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x_2}
e Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle y_2}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} m\ddot{x} & = & F_TC-F_nS\\ m\ddot{y} & = & F_TS+F_nC\\ m(\ddot{x}-b\ddot{\theta}S-b\dot{\theta}^2C) & = & -F_TC\\ m(\ddot{y}+b\ddot{\theta}C-b\dot{\theta}^2S) & = & -F_TS \end{array}}
Podemos reducir este sistema restando la tercera de la primera y la segunda de la cuarta para obtener
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} mb(\ddot{\theta}S+\dot{\theta}^2C) & = & 2F_TC-F_nS\\ mb(-\ddot{\theta}C+\dot{\theta}^2S) & = & 2F_TS+F_nC \end{array}}
Si ahora multiplicamos la primera por el coseno, la segunda por el seno y sumamos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle mb\dot{\theta}^2 = 2F_T}
y si multiplicamos la primera por el seno, la segunda por el coseno y restamos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle mb\ddot{\theta}=-F_n}
Esto nos permite eliminar las fuerzas de reacción vincular
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} m\ddot{x} & = & mb\left(\dfrac{\dot{\theta}^2C}{2}+\ddot{\theta}S\right)\\ m\ddot{y} & = & mb\left(\dfrac{\dot{\theta}^2S}{2}-\ddot{\theta}C\right) \end{array}}
Tenemos aqui dos ecuaciones con tres variables. Para completar el sistema hay que añadir la ecuación del vínculo no holónomo
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -S\dot{x}+C\dot{y}=0}
Hay que remarcar que aunque tengamos tres variables, el sistema tiene solo dos grados de libertad.
Ecuaciones de movimiento. Forma alternativa
Estas ecuaciones, o unas equivalentes, pueden obtenerse también empleando dos sistemas de referencia. Definimos un sistema de referencia ligado con origen en A y cuyo eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle OX_2}
va en la dirección de la varilla.
Posiciones
Empleando los dos sistemas, la posición de A es
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OA}=x\vec{\imath}_1+y\vec{\jmath}_1}
y la de B
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{AB}=b\vec{\imath}_2 \qquad\Rightarrow\qquad \overrightarrow{OB}=x\vec{\imath}_1+y\vec{\jmath}_1+b\vec{\imath}_2}
Velocidades
La velocidad de A es
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^A_{21}=\dot{x}\vec{\imath}_1+\dot{y}\vec{\jmath}_1}
Pero esta velocidad solo puede apuntar en la dirección de la varilla, por lo que debe ser de la forma
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^A_{21}=v\vec{\imath}_2}
cumpliéndose las relaciones
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{x}=v\cos(\theta)\qquad\qquad \dot{y}=v\,\mathrm{sen}(\theta)}
La velocidad de B cumple
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^B_{21}=\vec{v}^A_{21}+\vec{\omega}_{21}\times\overrightarrow{AB}=v\vec{\imath}+\omega b\vec{\jmath}_2}
siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \omega=\dot{\theta}}
la velocidad angular con que gira la varilla. Se cumple
Aceleraciones
Derivando la expresión de la velocidad de A obtenemos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^A_{21}=\dot{v}\vec{\imath}_2+v\frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}=\dot{v}\vec{\imath}_2+v\omega\vec{\jmath}_2}
ya que
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}=\vec{\omega}_{21}\times\vec{\imath}_2=\omega\vec{\jmath}_2}
La aceleración de B cumple
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^B_{21}=\vec{a}^A_{21}+\alpha_{21}\vec{k}\times\overrightarrow{AB}-\omega_{21}^2\overrightarrow{AB}= \dot{v}\vec{\imath}_2+v\omega\vec{\jmath}_2+\dot{\omega}b\vec{\jmath}_2-\omega^2b\vec{\imath}_2}
Agrupando términos queda
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}^B_{21}=(\dot{v}-\omega^2b)\vec{\imath}_2+(\omega v+\dot{\omega}b)\vec{\jmath}_2}
Ecuaciones de movimiento
La única fuerza que actúa sobre la masa B es la tensión de la varilla, por lo que
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m(\dot{v}-\omega^2b)\vec{\imath}_2+m(\omega v+\dot{\omega}b)\vec{\jmath}_2=-F_T\vec{\imath}_2}
Igualando componente a componete
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m(\dot{v}-\omega^2b) = -F_T \qquad\qquad m(\omega v+\dot{\omega}b)=0}
Sobre la masa A actúan la tensión y la fuerza normal a la cuchilla
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\dot{v}\vec{\imath}_2+mv\omega\vec{\jmath}_2=F_T\vec{\imath}_2+F_n\vec{\jmath}_2}
Igualando componente a componente
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m\dot{v}=F_T\qquad\qquad m\omega v = F_n}
Si eliminamos la tensión entre la ecuación para A y la ecuación para B llegamos a
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m(2\dot{v}-\omega^2b)=0}
que junto con la ecuación
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m(\omega v+\dot{\omega}b)=0}
constituyen las ecuaciones de movimiento del sistema.
Sistema de ecuaciones de primer orden
El sistema anterior posee solución analítica, aunque es laboriosa. Una forma más práctica se abordarlo sería mediante una integración numérica. Para ésta, conviene que no aparezcan funciones trigonométricas, que son costosas computacionalmente.
La solución alternativa nos da directamente un sistema de ecuaciones de primer orden, al que también se puede llegar con la primera forma de obtener las ecuaciones de movimiento.
Despejando, tenemos el sistema de ecuaciones
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} \dot{v}&=&\dfrac{\omega^2b}{2}\\ && \\ \dot{\omega}&=&-\dfrac{\omega v}{b} \end{array} }
Este sistema nos permite hallar v y ω, dadas las condiciones iniciales.
Una vez que hemos integrado este sistema, la variación del ángulo de la varilla con el tiempo resulta de integrar
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}=\omega}
y, una vez que hayamos calculado θ hallamos x e y integrando las ecuaciones
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} \dot{x}&=&v\cos(\theta)\\ \dot{y}&=&v\,\mathrm{sen}(\theta) \end{array} }
Reuniendo todas las ecuaciones queda el sistema
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} \dot{v}&=&\dfrac{\omega^2b}{2}\\ && \\ \dot{\omega}&=&-\dfrac{\omega v}{b} \\ \dot{\theta}&=&\omega\\ \dot{x}&=&v\cos(\theta)\\ \dot{y}&=&v\,\mathrm{sen}(\theta) \end{array} }
Los valores iniciales de estas variables salen de las posiciones y velocidades iniciales de las dos partículas, de las cuales se pueden despejar estas 5 variables.
Podemos eliminar completamente las funciones trigonométricas, añadiendo una variable más. Si consideramos S y C como variables independientes se cumple
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dot{C}=-\omega S\qquad\qquad \dot{S}=\omega C}
lo que daría el sistema de 6 ecuaciones
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} \dot{v}&=&\dfrac{\omega^2b}{2}\\ && \\ \dot{\omega}&=&-\dfrac{\omega v}{b} \\ \dot{x}&=&vC\\ \dot{y}&=&vS\\ \dot{C}&=&-\omega S\\ \dot{S}&=&\omega C \end{array} }
que estaría listo para implementarlo en un programa de ordenador.
