Dos masas en un triángulo, Noviembre 2012 (G.I.C.)

Enunciado

Se tienen dos masas de magnitud M=100g situadas a una distancia d=10cm. Otra masa m=10g se sitúa en el vértice superior del triángulo equilátero de la figura. Calcula el módulo de la fuerza gravitatoria sobre la masa m.

Solución

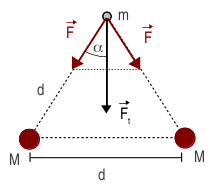
Como indica la figura, cada masa M atrae a la masa m con una fuerza dirigida hacia ella. La fuerza neta es la suma vectorial de estas dos fuerzas. Al hacer la suma vectorial, sólo queda la componente vertical de cada fuerza.

El módulo de la fuerza con que una masa M atrae a la masa m es

$|{\vec {F}}|={\dfrac {G\,M\,m}{d^{2}}}$

La proyección de esta fuerza sobre la vertical es

$F_{vert}=|{\vec {F}}|\cos \alpha ={\dfrac {G\,M\,m}{d^{2}}}\,\cos \alpha$

Como el triángulo es equilátero, el ángulo es $\alpha =\pi /6$. La fuerza total es la suma de las dos proyecciones.

$F_{m}=2\,F_{vert}={\dfrac {2\,G\,M\,m}{d^{2}}}\,\cos \alpha ={\dfrac {{\sqrt {3}}\,G\,M\,m}{d^{2}}}=12\times 10^{-12}\,\mathrm {N} =12\,\mathrm {pN}$