Dos masas en planos inclinados y un muelle

Enunciado

Dos masas iguales de peso Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle mg=75\,\mathrm{N}} situadas sobre dos planos inclinados contiguos, de las dimensiones mostradas en la figura. Las dimensiones son tales que el ángulo en O es recto.

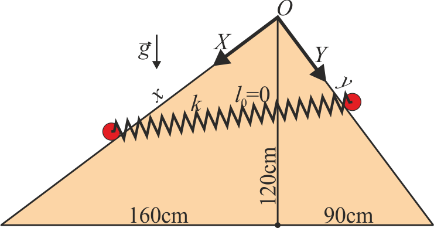
Las masas están unidas por un resorte ideal de longitud natural nula y constante $k=100\,\mathrm {N} /\mathrm {m}$. No hay rozamiento con las superficies.

1. Determine la posición de equilibrio de las dos masas, hallando los valores de $x$ e $y$.
2. Para esta posición de equilibrio, calcule las fuerzas de reacción ejercidas por los planos, así como la fuerza elástica que el resorte ejerce sobre cada masa.
3. Determine las ecuaciones de movimiento para las dos masas.

Posición de equilibrio

Por estar en equilibrio, la suma de las fuerzas sobre cada masa debe anularse.

Si llamamos masa “1” a la de la izquierda tenemos que las fuerzas que actúan sobre ella son:

Peso

que en los ejes indicados valen

$m{\vec {g}}=mg\,\mathrm {sen} (\alpha ){\vec {\imath }}+mg\cos(\alpha ){\vec {\jmath }}$

con

$\mathrm {tg} (\alpha )={\frac {120}{160}}={\frac {3}{4}}\qquad \Rightarrow \qquad \mathrm {sen} (\alpha )={\frac {3}{5}}\qquad \cos(\alpha )={\frac {4}{5}}$

lo que da el valor numérico

$m{\vec {g}}=75\left({\frac {3}{5}}{\vec {\imath }}+{\frac {4}{5}}{\vec {\jmath }}\right)\mathrm {N} =45{\vec {\imath }}+60{\vec {\jmath }}$

Fuerza elástica

Cuando la longitud natural de un resorte es nula, la fuerza elástica que produce la da la ley de Hooke vectorial es proporcional al vector de posición relativa. Si queremos hallar la fuerza en el extremo A, hallándose el otro extremo en el punto B

$F_{\mathrm {e1} }=-k{\overrightarrow {BA}}$

siendo ${\overrightarrow {BA}}$ el vector que va desde el extremo B del muelle hasta el A, que ocupa la partícula 1. En este caso sería

${\overrightarrow {OA}}=x{\vec {\imath }}\qquad \qquad {\overrightarrow {OB}}=y{\vec {\jmath }}$

Restando

${\overrightarrow {BA}}={\overrightarrow {OA}}-{\overrightarrow {OB}}=x{\vec {\imath }}-y{\vec {\jmath }}$

y por tanto

${\vec {F}}_{e1}=-kx{\vec {\imath }}+ky{\vec {\jmath }}=-100x{\vec {\imath }}+100y{\vec {\jmath }}$

Reacción normal del plano

Esta es perpendicular al plano y va en el sentido hacia afuera

${\vec {F}}_{n1}=-F_{n1}{\vec {\jmath }}$

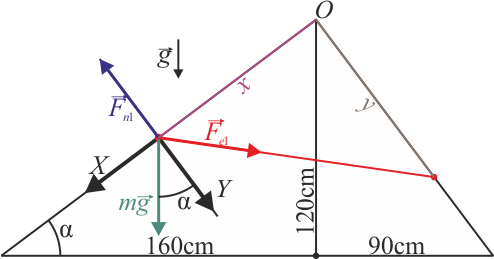
Sumando las tres fuerzas

$\left(mg\,\mathrm {sen} (\alpha ){\vec {\imath }}+mg\cos(\alpha ){\vec {\jmath }}\right)+\left(-kx{\vec {\imath }}+ky{\vec {\jmath }}\right)+\left(-F_{n1}{\vec {\jmath }}\right)={\vec {0}}$

y separando en componentes

$\left\{{\begin{array}{rcl}mg\,\mathrm {sen} (\alpha )-kx&=&0\\&&\\mg\cos(\alpha )+ky-F_{n1}&=&0\end{array}}\right.$

De aquí obtenemos de forma inmediata el valor de $x$ en el equilibrio

$x={\frac {mg\,\mathrm {sen} (\alpha )}{k}}={\frac {45}{100}}\,\mathrm {m} =45\,\mathrm {cm}$

Para obtener el valor de y hacemos el cálculo análogo para la segunda masa. Para esta

Peso

Al igual que antes

$m{\vec {g}}=mg\,\mathrm {sen} (\alpha ){\vec {\imath }}+mg\cos(\alpha ){\vec {\jmath }}$

Fuerza elástica

Aplicando el mismo razonamiento para esta masa o simplemente por la tercera ley de Newton

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_{e2}=-\vec{F}_{e1}=kx\vec{\imath}-ky\vec{\jmath}}

Reacción normal del plano

Esta es perpendicular al segundo plano

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_{n2}=-F_{n2}\vec{\imath}}

Sumando estas tres fuerzas

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left(mg\,\mathrm{sen}(\alpha)\vec{\imath}+mg\cos(\alpha)\vec{\jmath}\right)+\left(kx\vec{\imath}-ky\vec{\jmath}\right)+\left(F_{n2}\vec{\imath}\right)=\vec{0}}

que separando en componentes da

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\begin{array}{rcl} mg\,\mathrm{sen}(\alpha) + kx -F_{n2} & = & 0 \\ && \\ mg\cos(\alpha) - ky & = & 0 \end{array}\right.}

que nos da el valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y} en el equilibrio

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y = \frac{mg\,\mathrm{cos}(\alpha)}{k}=\frac{60}{100}\,\mathrm{m}=60\,\mathrm{cm}}

siendo la longitud del muelle

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle l= \sqrt{x^2+y^2}=\frac{mg}{k}\sqrt{\mathrm{sen}^2(\alpha)+\cos^2(\alpha)}=\frac{mg}{k}=75\,\mathrm{cm}}

Fuerzas de reacción

Una vez que tenemos x e y obtenemos las fuerzas normales

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_{n1}=mg\,\mathrm{sen}(\alpha)+ky=2mg\,\mathrm{sen}(\alpha)=90\,\mathrm{N}}

y

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_{n2}=mg\,\mathrm{cos}(\alpha)+kx=2mg\,\mathrm{cosn}(\alpha)=120\,\mathrm{N}}

En forma vectorial

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_{n1}=-2mg\,\mathrm{sen}(\alpha)\vec{\jmath}=-90\vec{\jmath}\,\mathrm{N}\qquad\qquad \vec{F}_{n2}=-2mg\,\mathrm{cos}(\alpha)\vec{\jmath}=-120\vec{\jmath}\,\mathrm{N}}

Cuando la figura se realiza correctamente a escala vemos que efectivamente el resorte no queda en una posición horizontal y que para cada masa, la suma vectorial de las tres fuerzas aplicadas es nula.

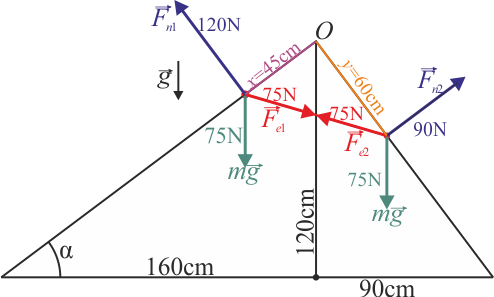
Ecuaciones de movimiento

Las ecuaciones de movimiento son inmediatas, ya que los desplazamientos son a lo largo de los planos, por lo que tenemos, para la masa 1

Definimos la elongación como la diferencia respecto a la posición de equilibrio calculada antes

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X=x -x_\mathrm{eq} = x - \frac{mg\,\mathrm{sen}(\alpha)}{k}\,}

y resulta la ecuación del oscilador armónico

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot{X}=-\frac{k}{m} X}

Por tanto, la masa 1 realiza oscilaciones de frecuencia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega=\sqrt{k/m}} alrededor de la posición de equilibrio.

Para la segunda masa el resultado es idéntico

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle ma_2= -k y +mg\,\cos(\alpha)}

Definimos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Y = y - y_\mathrm{eq}= y - \frac{mg\cos(\alpha)}{k}}

y resulta la misma ecuación del oscilador armónico

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot{Y}=-\frac{k}{m} Y}

Las dos masas oscilan con la misma frecuencia, pero indpendientemente la una de la otra.