Dos discos en varilla giratoria

Enunciado

Se tiene un sistema formado por dos discos idénticos, de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} y radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle R} (sólidos “2” y “3”). Los discos está montados sobre un eje común (sólido “0”), que es una varilla ideal de masa despreciable. La unión de los discos a la varilla es mediante rodamientos que permiten un giro libre alrededor del eje. La varilla, a su vez está articulada en una rótula a un eje vertical. El punto de articulación, O, no es el centro de la varilla, G, sino que está a una distancia $d$ del disco 2 y a una distancia Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle b} del disco 3. El sistema está sometido a la acción del peso y la posible fuerza de reacción en O. Tomamos un sistema de ejes rotatorio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0Y_0Z_0} en el que el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OZ_0} es el vertical y el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0} el que pasa por O y los centros de los dos discos. Todas las cantidades deben referirse a la base Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\vec{\imath}_0,\vec{\jmath}_0,\vec{k}_0 \right\}} . Supongamos que los discos giran respecto a su eje común, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0} , con velocidades angulares constantes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_2 \vec{\imath}_0} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_3 \vec{\imath}_0} , respectivamente, mientras la varilla gira respecto al eje vertical OZ_0 con velocidad angular constante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Omega\vec{k}_0} . Para un instante dado:

1. Determine las velocidades angulares de los dos discos respecto a un sistema fijo “1”, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{21}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{31}} .
2. Para cada disco determine su tensor de inercia respecto al sistema Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0Y_0Z_0} .
3. Calcule la cantidad de movimiento del sistema.
4. Halle el momento cinético respecto al punto O de cada disco y el total, suma de los dos,
5. Halle la energía cinética de cada disco y la total, suma de las dos.
6. Determine la relación que debe haber entre Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_2} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega_3} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Omega} en función de las masas, de g y de las dimensiones del sistema para que el sistema se mantenga girando uniformemente sin que sea preciso aplicar ningún par en O, de forma que el único momento sea el debido al peso.
7. Halle la fuerza de reacción en O.

    

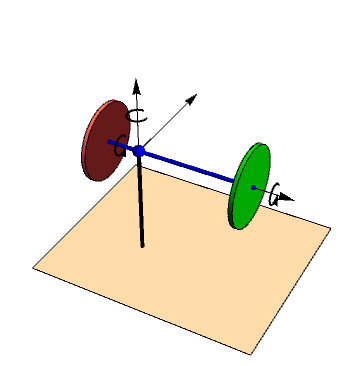
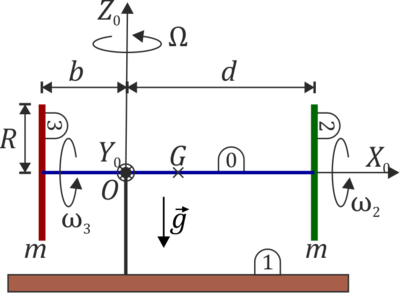
Velocidades angulares

Los datos que nos da el problema son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{01}=\Omega\vec{k}_0\qquad\qquad \vec{\omega}_{20}=\omega_2\vec{\imath}_0\qquad\qquad\vec{\omega}_{30}=\omega_3\vec{\imath}_0}

Por composición de velocidades

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}=\omega_2\vec{\imath}_0+\Omega\vec{k}_0}

y

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{31}=\vec{\omega}_{30}+\vec{\omega}_{01}=\omega_3\vec{\imath}_0+\Omega\vec{k}_0}

Tensores de inercia

El tensor de inercia de un disco respecto a unos ejes paralelos a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0y_0Z_0} por su centro es de la forma

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar{\bar{I}}^{A}=\bar{\bar{I}}^{B}=\frac{1}{4}mR^2\begin{pmatrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}}

siendo A el centro del disco 2 y B el del disco 3, con

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OA}=d\vec{\imath}_0\qquad\qquad \overrightarrow{OB}=-b\vec{\imath}_0}

Aquí se ha aplicado que el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle AX_0} es perpendicular por el centro del disco

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I^{A}_{xx}=\frac{1}{2}mR^2}

y los ejes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle AZ_0} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle AY_0} son paralelos a una superficie plana e iguales entre sí

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I^{A}_{yy}=I^{A}_{yy}\qquad\qquad I^{A}_{yy}+I^{A}_{zz}=I^{A}_{xx}\qquad\Rightarrow\qquad I^{A}_{yy}=I^{A}_{yy}=\frac{1}{4}mR^2}

Para llevar este tensor al punto O aplicamos el teorema de Steiner

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar{\bar{I}}_2^O=\bar{\bar{I}}^{A}+m\begin{pmatrix} y_A^2+z_A^2 & -x_Ay_A & -x_Az_A \\ -x_Ay_A & x_A^2+z_A^2 & -y_Az_A \\ -x_Az_A & -y_Az_A & x_A^2+y_A^2\end{pmatrix}=\frac{1}{4}mR^2\begin{pmatrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}+md^2\begin{pmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}=\begin{pmatrix} \dfrac{mR^2}{2} & 0 & 0 \\ 0 & m\left(\dfrac{R^2}{4}+d^2\right) & 0 \\ 0 & 0 & m\left(\dfrac{R^2}{4}+d^2\right)\end{pmatrix}}

Y de la misma manera para el disco 3

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \bar{\bar{I}}_3^O=\begin{pmatrix} \dfrac{mR^2}{2} & 0 & 0 \\ 0 & m\left(\dfrac{R^2}{4}+b^2\right) & 0 \\ 0 & 0 & m\left(\dfrac{R^2}{4}+b^2\right)\end{pmatrix}}

Cantidad de movimiento del sistema

Para un sistema de partículas

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{p}=m_T\vec{v}_G}

con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m_T} la masa total

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m_T=2m\,}

y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_G} la velocidad del CM respecto a un sistema fijo. En este caso el CM pertenece a la varilla “0” y se halla en la posición

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{OG}=\frac{m\overrightarrow{OA}+m\overrightarrow{OB}}{2m}=\frac{d-b}{2}\vec{\imath}_0}

siendo su velocidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^G_{01}=\vec{\omega}_{01}\times\overrightarrow{OG}=(\Omega\vec{k}_0)\times\left(\frac{d-b}{2}\vec{\imath}_0\right)=\frac{\Omega(d-b)}{2}\vec{\jmath}_0}

Por tanto la cantidad de movimiento del sistema es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{p}=(2m)\frac{\Omega(d-b)}{2}\vec{\jmath}_0=m\Omega(d-b)\vec{\jmath}_0}

Momento cinético

Por ser O un punto fijo, el momento cinético del disco 2 se puede calcular como

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{L}_{2O}=\bar{\bar{I}}^O_2\cdot\vec{\omega}_{21}=\begin{pmatrix} \dfrac{mR^2}{2} & 0 & 0 \\ 0 & m\left(\dfrac{R^2}{4}+d^2\right) & 0 \\ 0 & 0 & m\left(\dfrac{R^2}{4}+d^2\right)\end{pmatrix}\cdot\begin{pmatrix}\omega_2\\ 0\\ \Omega\end{pmatrix}=\frac{mR^2}{2}\omega_2\vec{\imath}_0+\left(\frac{1}{4}mR^2+md^2\right)\Omega\vec{k}_0}

y de la misma manera para el 3

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{L}_{3O}=\frac{mR^2}{2}\omega_3\vec{\imath}_0+\left(\frac{1}{4}mR^2+mb^2\right)\Omega\vec{k}_0}

siendo el momento cinético total

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{L}_O=\frac{mR^2}{2}(\omega_2+\omega_3)\vec{\imath}_0+\left(\frac{1}{2}mR^2+mb^2+md^2\right)\Omega\vec{k}_0}

Energía cinética

Por ser O un punto fijo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T_2=\frac{1}{2}\vec{\omega}_{21}\cdot\vec{L}_{2O}=\frac{1}{2}\vec{\omega}_{21}\cdot\bar{\bar{I}}^O_2\cdot\vec{\omega}_{21}=\frac{mR^2}{4}\omega_2^2+\frac{1}{2}\left(\frac{1}{4}mR^2+md^2\right)\Omega^2}

y para el disco 3

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T_3=\frac{mR^2}{4}\omega_3^2+\frac{1}{2}\left(\frac{1}{4}mR^2+mb^2\right)\Omega^2}

La energía cinética total del sistema vale, sumando y agrupando términos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T=T_2+T_3=\frac{mR^2}{4}(\omega_2^2+\omega_3^2+\Omega^2)+\frac{m(d^2+b^2)}{2}\Omega^2}

Momento de las fuerzas

Para que el sistema se mantenga en equilibrio sin inclinarse debe cumplirse el teorema del momento cinético

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_O}

con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{M}_O} el momento de las fuerzas externas, en este caso el peso. Este momento vale

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{M}_O=\overrightarrow{OG}\times(m_T\vec{g})=\frac{d-b}{2}\vec{\imath}_0\times (-2m\vec{k}_0)=m(b-d)g\vec{\jmath}_0}

Por su parte, la derivada del momento cinético en el sistema fijo vale

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1=\left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_0+\vec{\omega}_{01}\times\vec{L}_O}

En el sistema 0 la derivada temporal es nula, ya que el cálculo que hemos efectuado para hallar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{L}_0} en la base Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\vec{\imath}_0,\vec{\jmath}_0,\vec{k}_0 \right\}} produce un vector de coeficientes constantes. Por tanto queda solo el segundo término

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1=\vec{\omega}_{01}\times\vec{L}_O=(\Omega\vec{k}_0)\times\left(\frac{mR^2}{2}(\omega_2+\omega_3)\vec{\imath}_0+\left(\frac{1}{2}mR^2+mb^2+md^2\right)\Omega\vec{k}_0\right)=\frac{mR^2}{2}(\omega_2+\omega_3)\Omega\vec{\jmath}_0}

Como esta cantidad debe ser igual al momento del peso llegamos a la relación

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{mR^2}{2}(\omega_2+\omega_3)\Omega\vec{\jmath}_0=m(b-d)g\vec{\jmath}_0\qquad\Rightarrow\qquad (\omega_2+\omega_3)\Omega = \frac{2(b-d)g}{R^2}}

Fuerza en el punto de apoyo

Aplicamos el teorema de la cantidad de movimiento

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left.\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\right|_1=\vec{F}_O+m\vec{g}}

Aplicamos el mismo razonamiento que en el apartado anterior para la derivada respecto al tiempo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_O=\vec{\omega}_{01}\times\vec{p}-m\vec{g}=\left(\Omega\vec{k}_0\right)\times\left(m\Omega(d-b)\vec{\jmath}_0\right)-\left(-2mg\vec{k}_0\right)=-m(d-b)\Omega^2\vec{\imath}_0+2mg\vec{k}_0}

El primer término no representa otra cosa que la fuerza normal que produce el movimiento circular del CM alrededor de O.