Dos discos dentro de una corona (CMR)

Enunciado

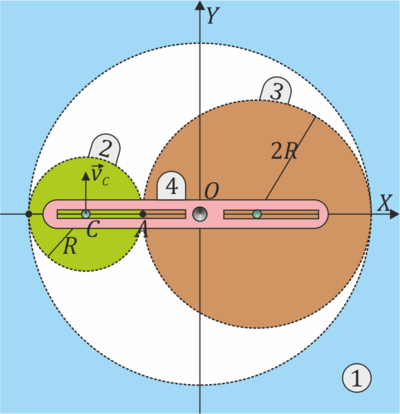
En el interior de un hueco circular (“1”) de radio 3R se encuentran dos discos (“2” y “3”) del mismo espesor y densidad de masa, de radios R y 2R, respectivamente, siendo sus masas $m_{2}=m$ y $m_{3}=4m$. Una varilla (“4”) de masa despreciable une sus centros. Los dos discos están articulados sin rozamiento en la varilla. Los discos ruedan sin deslizar sobre la pared del hueco, de manera que en todo momento dado la velocidad del centro del disco pequeño respecto al aro exterior es ${\vec {v}}_{21}^{C}=v_{0}{\vec {\jmath }}_{4}$.

1. Determine las velocidades angulares ${\vec {\omega }}_{21}$, ${\vec {\omega }}_{31}$, ${\vec {\omega }}_{41}$ y ${\vec {\omega }}_{32}$
2. Determine la velocidad de deslizamiento de un disco respecto a otro en el punto de contacto A, ${\vec {v}}_{23}^{A}$.
3. Halle la energía cinética del sistema y el momento cinético respecto al centro del sistema, O.

Dato: Momento de inercia de un disco alrededor de un eje perpendicular a él que pasa por su centro: $I=mR^{2}/2$.

Velocidades angulares

El disco “2” rueda sobre la corona, de manera que el punto B de contacto tiene velocidad nula. Aplicando la expresión del campo de velocidades

$v_{0}{\vec {\jmath }}_{4}={\vec {v}}_{21}^{C}=\overbrace {{\vec {v}}_{21}^{B}} ^{={\vec {0}}}+\left(\omega _{21}{\vec {k}}\right)\times (R{\vec {\imath }}_{4})=\omega _{21}R{\vec {\jmath }}_{4}$

Por ello

${\vec {\omega }}_{21}={\frac {v_{0}}{R}}{\vec {k}}$

De la misma manera, para la varilla 4, a la cual también pertenece el punto C, gira alrededor del centro O.

$v_{0}{\vec {\jmath }}_{4}={\vec {v}}_{41}^{C}=\overbrace {{\vec {v}}_{41}^{O}} ^{={\vec {0}}}+\left(\omega _{41}{\vec {k}}\right)\times (-2R{\vec {\imath }}_{4})=-2\omega _{21}R{\vec {\jmath }}_{4}$

Por ello

${\vec {\omega }}_{41}=-{\frac {v_{0}}{2R}}{\vec {k}}$

Esto nos da la velocidad del centro D del disco grande, también unido a la varilla

${\vec {v}}_{31}^{D}={\vec {v}}_{41}^{D}\overbrace {{\vec {v}}_{41}^{O}} ^{={\vec {0}}}+\left(-{\frac {v_{0}}{2R}}{\vec {k}}\right)\times (R{\vec {\imath }}_{4})=-{\frac {v_{0}}{R}}{\vec {\jmath }}_{4}$

Este disco 3 rueda sobre el punto de contacto E, lo que nos da la velocidad angular de este disco respecto a la corona.

$-{\frac {v_{0}}{2}}{\vec {\jmath }}_{4}={\vec {v}}_{31}^{D}=\overbrace {{\vec {v}}_{31}^{D}} ^{={\vec {0}}}+\left(\omega _{31}{\vec {k}}\right)\times (-2R{\vec {\imath }}_{4})=-2\omega _{21}R{\vec {\jmath }}_{4}$

Por ello

${\vec {\omega }}_{31}={\frac {v_{0}}{4R}}{\vec {k}}$