Disco girando sujeto por un muelle, Enero 2015 (G.I.C.)

Enunciado

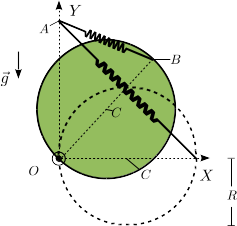
Un disco homógeneo de masa $M$ y radio $R$ puede girar en torno al punto $O$ de su borde. El extremo superior del disco está unido al punto $A$ con un resorte ideal de longitud natural nula y constante elástica $k$. En el instante inicial se encuentra en posición vertical, de modo que el punto $B$ del disco coincide con el punto $A$ donde está anclado el resorte. En $t=0$ empieza a girar hacia la derecha, de modo que su velocidad angular inicial es 0.

1. Sabiendo que el momento de inercia del disco respecto a un eje perpendicular a su plano que pasa por su centro es $MR^{2}/2$, determina el momento de inercia respecto a un eje perpendicular a su plano que pasa por el punto $O$.
2. Calcula la velocidad del centro del disco $C$ en el instante en el que está sobre el eje $X$.

Solución

Momento de inercia

El teorema de los ejes paralelos (o de Steiner) dice que, dado el momento de inercia respecto a un eje que pase por el centro de masas, $I_{CM}$, el momento de inercia respecto a otro eje paralelo a él, $\Delta$separado una distancia $h$ del primero es

$I_{\Delta }=I_{CM}+M\Delta ^{2}$

En este caso tenemos $I_{CM}={\dfrac {1}{2}}MR^{2}$. El eje $\Delta$ pasa por $O$, por lo que la distancia entre los dos ejes es$h=R$. Por tanto

$I_{O}=I_{CM}+MR^{2}={\dfrac {1}{2}}MR^{2}+MR^{2}={\dfrac {3}{2}}MR^{2}$

Velocidad del centro

Lo resolvemos usando la conservación de energía mecánica. Las únicas fuerzas que realizan trabajo sobre el disco son el peso y el muelle. La fuerza de reacción vincular en el punto $O$ no realiza trabajo. Entonces la energía mecánica se conserva. Tomamos como origen de energía potencial gravitatoria el eje $OX$. En el instante inicial, cuando el punto $B$ del disco coincide con el punto $A$, la energía cinética es cero y el muelle está totalmente contraído (tiene longitud natural nula). Entonces la energía mecánica es igual a la energía potencial gravitatoria

$E=MgR$

Es la posición del centro de masas del disco la que determina la energía potencial gravitatoria.

Cuando el centro del disco está sobre el eje $OX$, la energía potencial gravitatoria es nula. El disco gira con una velocidad angular $\omega$, por lo que su energía cinética de rotación es

$T={\dfrac {1}{2}}I_{O}\omega ^{2}$

La energía potencial elástica del muelle es

$U_{k}={\dfrac {1}{2}}k((2R)^{2}+(2R)^{2})=4kR^{2}$

La energía mecánica en este instante es

$E={\dfrac {1}{2}}I_{O}\omega ^{2}+4kR^{2}$

Igualando con la expresión inicial de la energía mecánica tenemos

$mgR={\dfrac {1}{2}}I_{O}\omega ^{2}+4kR^{2}$

Despejando la velocidad de rotación, y teniendo en cuenta el valor de $I_{O}$ del apartado anterior, tenemos

$\omega ^{2}={\dfrac {4g}{3R}}\,\left(1-{\dfrac {4kR}{Mg}}\right)$

La velocidad angular y la velocidad del punto $C$ se relacionan por

$v_{C}=\omega R$

Por tanto, la velocidad de $C$ es

$v_{C}={\sqrt {{\dfrac {4gR}{3}}\,\left(1-{\dfrac {4kR}{Mg}}\right)}}$