Enunciado
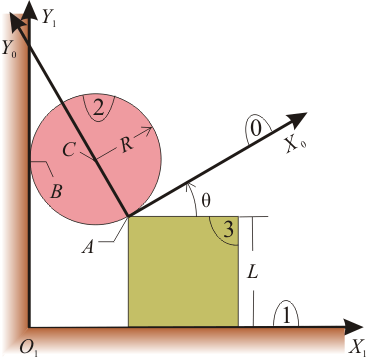
El sistema mecánico de la figura está constituido por los siguientes sólidos rígidos: El plano fijo (sólido “1”); la placa cuadrada, de lado , que desliza sobre el eje , manteniendo su lado inferior completo en permanente contacto con él (sólido “3”); el disco, de centro en C y radio , que, en todo instante, rueda sin deslizar sobre el eje en el punto de contacto B, a la vez que rueda y desliza sobre la placa cuadrada en el punto de contacto A (sólido “2”) y el sistema de ejes , definido de tal modo que el eje contiene permanentemente al centro C del disco, mientras que el eje es tangente a dicho disco (sólido “0”).
- Para el instante considerado en la figura, determine gráficamente la posición de los centros instantáneos de rotación , , , e .
- Utilizando como parámetro el ángulo del dibujo (ángulo que forma el eje con respecto al lado superior de la placa cuadrada), y teniendo presentes las leyes de composición de velocidades y de velocidades angulares aplicadas a {21} = {20} + {03} + {31} halle las siguientes reducciones cinemáticas en C: , , y .
Centros instantáneos de rotación
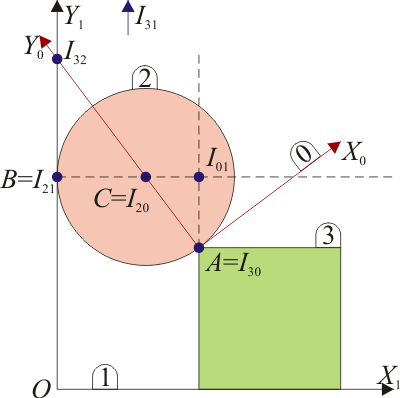
Tenemos aquí cuatro sólidos y por tanto 6 centros instantáneos de rotación. Algunos de ellos son evidentes, otros requieren el uso del teorema de los tres centros.
- Movimiento {21}
- Dado que el disco rueda sin deslizar sobre la pared vertical, el CIR es el punto de contacto B entre el disco y la pared
- Movimiento {20}
- El punto C es un un punto material del disco “2” que ocupa una posición fija en el sistema “0” por cómo está definido éste. Al ser nula la velocidad , este punto es el CIR de este movimiento
- Movimiento {30}
- Ocurre lo mismo que en el caso anterior, pero con el punto A: es un punto del sólido 3 que ocupa una posición fija en el sistema “0”. Por ello
- Movimiento {31}
- La placa se está trasladando horizontalmente. Por tanto, su centro instantáneo de rotación se encuentra situado en el infinito, según la dirección perpendicular a la velocidad, que en este caso es la que tomamos como vertical.
- Movimiento {01}
- Por el teorema de los tres centros se encuentra alineado con el y el . Por tanto se halla sobre la recta horizontal que pasa por C. Por el mismo teorema, se encuentra alineado con el y el . Por ello, se encuentra sobre la vertical que pasa por A. La intersección de estas dos rectas nos da el CIR
- Movimiento {32}
- Para este punto aplicamos de nuevo dos veces el teorema de los tres centros. está alineado con e , esto es se halla sobre la recta que pasa por A y C. Asimismo, se encuentra alineado con e , es decir, está en la recta vertical que pasa por B, el eje . La intersección de las dos rectas da el CIR buscado, .
Reducciones cinemáticas
Para las reducciones cinemáticas necesitamos hallar cuatro velocidades angulares y cuatro velocidades lineales del punto C. Puesto que el cálculo de cada una implica ir hallando simultáneamente el resto, calcularemos las diferentes cantidades de forma un tanto desordenada, y al final tabularemos los distintos resultados.
Comenzamos por el dato más sencillo: la velocidad de C en el movimiento {20} es nula, por tratarse del CIR de este movimiento
También es un dato la velocidad angular en el movimiento {03}
Sabemos asimismo que el movimiento {31} es una traslación, por lo que
Esto nos permite hallar la velocidad angular en {01}
Para obtener el resto de las cantidades usaremos, como indica el enunciado, la descomposición {21} = {20} + {03} + {31}. Consideremos el punto C, respecto al cual se nos piden las diferentes reducciones. La ley de composición de velocidades nos dice
Analicemos cada uno de estos sumandos:
- Velocidad de C en {21}
- Esta consiste en una rotación en torno al punto B, con una velocidad angular que por ahora no conocemos
- Velocidad de C en {20}
- Es nula, por tratarse del CIR de este movimiento
- Velocidad de C en {03}
- Esta es una rotación alrededor de A con velocidad angular
- Este resultado está en expresado en la base “0”. Si lo pasamos a la base “1” queda
- Velocidad de C en {31}
- Este movimiento es una traslación horizontal
Sumando los distintos términos e igualando nos queda
Puesto que dos vectores son iguales si lo son sus componentes respectivas
Esto nos permite hallar las dos cantidades desconocidas
Por último, hallamos la velocidad angular {20}
Con toda esta información, ya podemos enunciar las diferentes reducciones cinemáticas.
- Movimiento {20}
- En este movimiento C está en reposo y la velocidad angular es la que acabamos de calcular, por tanto
- Movimiento {03}
- En el movimiento {03} C efectúa una rotación en torno a A, tal que
- Movimiento {31}
- En el movimiento {31} C se está trasladando horizontalmente
- Movimiento {21}
- Por último, el movimiento {21} es una rotación alrededor de B












































