Dinámica de la partícula no vinculada (CMR)

Definición

Una partícula no vinculada es aquella que puede moverse sin obstáculo en las tres direcciones del espacio, aunque puede estar sometida a fuerzas que afectan a su movimiento.

El que pueda describir tres movimientos independientes, y por tanto para especificar su posición se requieran tres coordenadas se expresa diciendo que la partícula tiene 3 grados de libertad.

$\mathrm {GDL} =N=3\,$

El número de grados de libertad se expresa como GDL o D.O.F. (degrees of freedom).

El problema fundamental de la dinámica

Determinación de posiciones

En esencia, el problema que se plantea al estudiar la partícula no vinculada es ¿cómo se mueve esto? Es decir, se conoce el estado inicial (posición y velocidad) de la partícula y se conocen las fuerzas que actúan sobre ella (a partir de alguna ley de fuerza: gravitación, electromagnetismo, fuerzas elásticas,…) y a partir de ahí se trata de determinar su posición en un instante posterior.

Matemáticamente se trata de plantear la ecuación de movimiento

${\vec {a}}={\dfrac {1}{m}}{\vec {F}}({\vec {r}},{\vec {v}},t)$

o, en forma de ecuación diferencial

${\frac {\mathrm {d} ^{2}{\vec {r}}}{\mathrm {d} t}}={\dfrac {1}{m}}{\vec {F}}\left({\vec {r}},{\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}},t\right)$

A esta euación hay que añadir las condiciones iniciales

${\vec {r}}(t=0)={\vec {r}}_{0}\qquad \qquad {\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}(t=0)={\vec {v}}(t=0)={\vec {v}}_{0}$

Obsérvese que suponemos que la fuerza depende de la posición, la velocidad y el tiempo, pero no de la propia aceleración. Eso es una evidencia física. Cuando se suponen fuerzas dependientes de la aceleración se obtienen resultados físicamente absurdos.

Desde el punto de vista del cálculo es más útil escribir la ecuación de movimiento como ecuaciones diferenciales de primer orden, con lo que queda

${\begin{array}{rcl}{\dfrac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}&=&{\vec {v}}\\&&\\{\dfrac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}&=&{\dfrac {1}{m}}{\vec {F}}({\vec {r}},{\vec {v}},t)\end{array}}$

con las condiciones iniciales

${\vec {r}}(t=0)={\vec {r}}_{0}\qquad \qquad {\vec {v}}(t=0)={\vec {v}}_{0}$

Considerando que cada vector tiene tres componentes, esto son seis ecuaciones diferenciales de primer orden acopladas (es decir, que no se pueden resolver independientemente, ya que la solución de cada una depende de las demás).

Hay ocasiones en que la solución es trivial (caso de una fuerza constante), en otras existen soluciones analíticas más o menos complejas, pero en la mayoría de los casos la solución de las ecuaciones de movimiento requiere el cálculo numérico. Un ejemplo famoso es el del problema de los tres cuerpos. El movimiento de un cuerpo como un satélite en el campo gravitatorio de otros dos, como la Tierra y la Luna, no puede resolverse analíticamente.

Determinación de fuerzas

No siempre la dinámica de la partícula no vinculada consiste en predecir el movimiento de ésta. En otras ocasiones lo que se conoce es el movimiento (de manera experimental) y el objetivo es determinar la fuerza.

Así, por ejemplo, a partir de las tres leyes de Kepler, empíricas, Newton llegó a la ley de la Gravitación Universal.

Introducción a la solución numérica

Como se ha dicho, en la mayoría de los problemas reales, las ecuaciones de movimiento deben resolverse numéricamente. Para ello existen una gran diversidad de métodos, tanto de aplicación general como específicos para problemas concretos.

A la hora de resolver un problema de este tipo, suele ser interesante seguir un cierto protocolo:

• Elegir las unidades adecuadas que simplifiquen el problema al máximo, reciendo al mínimo el número de parámetros independientes.
• Escribir las ecuaciones de movimiento como un sistema de ecuaciones de primer orden.
• Reducir, cuando sea posible, la complejidad algebraica de las ecuaciones, procurando evitar funciones que requieran tiempo de cálculo elevado.
• Elegir un paso de tiempo progresivamente más pequeño, hasta alcanzar la precisión deseada.

A continuación explicamos la idea de algúnos métodos simples de aplicación general.

El método de Euler

La idea del método de Euler es simple. Si conocemos la posición, la velocidad y la aceleración en un instante dado, podemos hallar la posición y la velocidad en un instante posterior, suponiendo que la velocidad y la aceleración son prácticamente constantes (lo cual será más o menos cierto si el intervalo de tiempo es muy corto). Con la nueva posición y velocidad, hallamos el nuevo valor de la fuerza y de aquí la nueva aceleración. Repetimos el proceso todas las veces que haga falta.

Matemáticamente el método es el siguiente. Las ecuaciones de movimiento pueden escribirse como dos ecuaciones para las primeras derivadas

${\begin{array}{rcl}\displaystyle {\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}&=&{\vec {v}}\\&&\\\displaystyle {\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}&=&\displaystyle {\frac {1}{m}}{\vec {F}}({\vec {r}},{\vec {v}},t)\end{array}}$

Hacemos entonces la aproximación siguiente: una derivada no es más que un cociente entre dos incrementos infinitamente pequeños. Aproximamos entonces las derivadas por incrementos finitos

${\begin{array}{rcl}\displaystyle {\frac {\Delta {\vec {r}}}{\Delta t}}&\simeq &{\vec {v}}\\&&\\\displaystyle {\frac {\Delta {\vec {v}}}{\Delta t}}&\simeq &\displaystyle {\frac {1}{m}}{\vec {F}}({\vec {r}},{\vec {v}},t)\end{array}}$

Teniendo en cuenta que

$\Delta {\vec {r}}={\vec {r}}(t+\Delta t)-{\vec {r}}(t)\qquad \Delta {\vec {v}}={\vec {v}}(t+\Delta t)-{\vec {v}}(t)$

podemos despejar

${\begin{array}{rcl}\displaystyle {\vec {r}}(t+\Delta t)&\simeq &{\vec {r}}(t)+{\vec {v}}(t)\Delta t\\&&\\\displaystyle {\vec {v}}(t+\Delta t)&\simeq &\displaystyle {\vec {v}}(t)+{\frac {\Delta t}{m}}{\vec {F}}({\vec {r}}(t),{\vec {v}}(t),t)\end{array}}$

Si etiquetamos las sucesivas posiciones y velocidades por un subíndice, nos queda la sucesión

${\begin{array}{rcl}t_{n+1}&=&t_{n}+h\\&&\\\displaystyle {\vec {r}}_{n+1}&=&{\vec {r}}_{n}+{\vec {v}}_{n}h\\&&\\\displaystyle {\vec {v}}_{n+1}&=&\displaystyle {\vec {v}}_{n}+{\frac {h}{m}}{\vec {F}}_{n}\end{array}}$

que nos proporciona una tabla de valores de la posición y la velocidad para una lista de valores del tiempo.

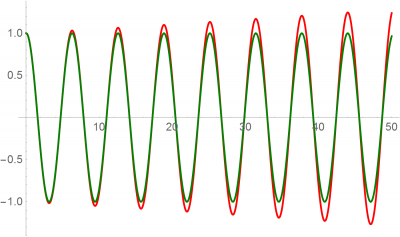
¿Cuál es el riesgo del método? Que si la aproximación no es buena, la posición y la velocidad calculadas pueden ser ligeramente errónea, lo que nos dará una fuerza también incorrecta. Esto nos producirá una nueva posición y velocidad aun más incorrecta, y así sucesivamente. Los errores se van acumulando y podemos acabar muy lejos de donde deberíamos estar.

Como ilustración consideremos el caso de un oscilador armónico en una dimensión, que tiene por ecuaciones de movimiento

${\dot {x}}=v\qquad {\dot {v}}=-{\frac {k}{m}}x$

con condiciones iniciales $x(0)=A$, $v(0)=0$ Este sistema tiene solución analítica, por lo que puede verse cómo de buena es una aproximación.

Lo primero es elegir unidades adecuadas. Si $x_{0}$, $t_{0}$ y $v_{0}$ son las unidades

$x=x_{0}x^{*}\qquad \qquad t=t_{0}t^{*}\qquad \qquad v=v_{0}v^{*}$

el sistema se convierte en (quitando los asteriscos)

${\dot {x}}={\frac {v_{0}t_{0}}{x_{0}}}v\qquad \qquad {\dot {v}}=-{\frac {kx_{0}t_{0}}{mv_{0}}}x\qquad x(0)={\frac {A}{x_{0}}}\qquad v(0)=0$

que se simplifica al máximo si hacemos

$x_{0}=A\qquad \qquad t_{0}={\sqrt {\frac {m}{k}}}\qquad \qquad v_{0}={\frac {x_{0}}{t_{0}}}$

de forma que el sistema se reduce a

${\dot {x}}=v\qquad \qquad {\dot {v}}=-x\qquad \qquad x(0)=1\qquad \qquad v(0)=0$

Para un $\Delta t$ grande (puntos rojos) resultan oscilaciones, pero que se separan rápidamente de la solución exacta (línea verde). Reduciendo el intervalo de tiempo (puntos azules) se obtiene una mejor aproximación. El coste de esta precisión es que requiere más cálculos y por tanto mayor tiempo de computación. Es necesario entonces hallar un balance entre la precisión deseada y los recursos disponibles.

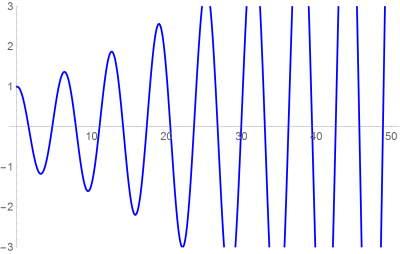
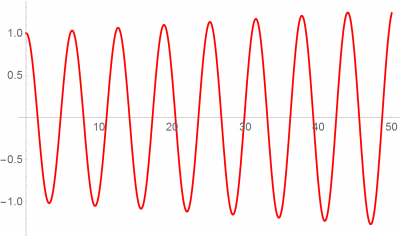
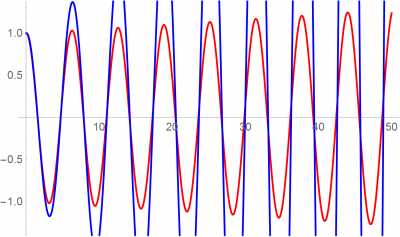
El método de Euler es muy poco preciso y por ello no se usa en la práctica. Existen métodos mucho más refinados, como el Runge-Kutta, que con el mismo número de operaciones produce una mucha mejor aproximación al resultado.

El método de Runge-Kutta

La idea de los métodos de Runge-Kutta es en primer lugar extrapolar como en el método de Euler, pero luego emplear el valor de la derivada en el punto de destino para hallar una nueva extrapolación mejorada. El proceso se puede repetir varias veces, obteniendo mejores grados de aproximación.

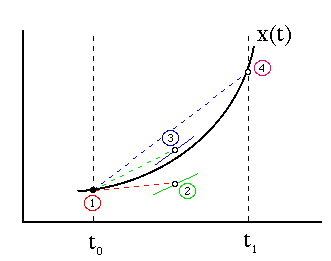
Existen diveros métodos de Runge-Kutta, según el grado de aproximación que se desee. La variante más común es el de cuarto orden. En esta variante se escribe el sistema de ecuaciones de primer orden

${\dot {x}}=f(x,t)$

donde $x$ es un vector que contiene todas las variables, salvo el tiempo (es decir, para una partícula no vinculada tendría 6 componentes: las tres de la posición y las tres de la velocidad. Se define un paso de tiempo $h$ y dado el estado n, se calcula el n+1 como

${\begin{array}{rcl}k_{1}&=&hf(x_{n},t_{n})\\k_{2}&=&hf(x_{n}+k_{1}/2,t_{n}+h/2)\\k_{3}&=&hf(x_{n}+k_{2}/2,t_{n}+h/2)\\k_{4}&=&hf(x_{n}+k_{3},t_{n}+h)\\t_{n+1}&=&t_{n}+h\\x_{n+1}&=&x_{n}+{\dfrac {k_{1}+2k_{2}+2k_{3}+k_{4}}{6}}\end{array}}$

El método de Runge-Kutta es explícito como el de Euler (es decir, conocido el estado actual podemos hallar el siguiente estado sin más información que la función $f(x,t)$). La precisión de cada paso es de orden $h^{5}$, es decir, que si tomamos un paso de 0.1, se alcanza una precisión de 0.00001. Teniendo en cuenta que el número de pasos totales es inversamente proporcional a la duración del paso, la precisión del resultado final es de orden $h^{4}$.

Existen mejoras a este método. Una de ellas es emplear el paso ajustable. En lugar de emplear un $h$ fijo se hace cada iteración con el valor del paso anterior. Se vuelve a hacer el cálculo con un Runge-Kutta de 5º orden, más preciso. A partir de la diferencia se fija el siguiente valor de h (más pequeño si diferen mucho, más largo si son muy próximos). En este caso, como se hacen dos pasadas para los puntos, una de orden 4 y otra de orden 5, el método se dice que es (4,5). Esta es la variante que implementa Matlab en su función ode45.