Cono rotando con punto fijo (Nov. 2018)

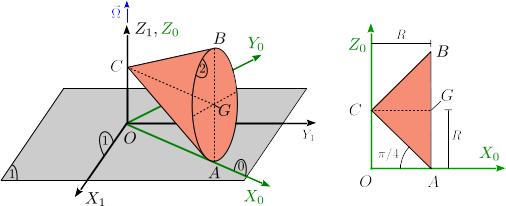
Enunciado

Un cono con ángulo de abertura $\pi /4$ y radio de la base $R$ se mueve de modo que rueda sin deslizar sobre el plano fijo "1" y su vértice $C$ permanece fijo sobre el eje $OZ_{1}$. La base del cono permanece siempre perpendicular al plano $OX_{1}Y_{1}$. El sólido auxiliar "0" se escoge de modo que el plano $X_{0}Z_{0}$ contiene siempre a los puntos $A$, $B$ y $C$ del cono. El sólido "0" rota alrededor del eje $OZ_{1}$ con velocidad angular constante ${\vec {\Omega }}=\Omega \,{\vec {k}}_{0,1}$.

1. Localiza y dibuja los ejes de rotación de los movimientos {01}, {20} y {21}. ¿Qué tipo de eje es cada uno de ellos?
2. Calcula las reducciones cinemáticas en $G$ de los tres movimientos relativos.
3. Calcula las derivadas temporales de las reducciones cinemáticas en $G$ de los tres movimientos relativos.

Solución

Análisis del enunciado

De los datos del enunciado podemos deducir los siguientes hechos:

1. El cono rueda sin desliar sobre el plano, por tanto ${\vec {v}}_{21}^{\,A}={\vec {0}}$.
2. El punto $C$ es fijo sobre el eje $OZ_{1}$. Entonces ${\vec {v}}_{21}^{\,C}={\vec {0}}$.
3. Del dibujo vemos que el movimiento {01} es un par de revolución con ${\vec {v}}_{01}^{\,O}={\vec {0}}$ y ${\vec {\omega }}_{01}=\Omega \,{\vec {k}}_{0,1}$.
4. También relacionado con este movimiento vemos que el centro de la base del cono no se mueve respecto al plano $OX_{0}Z_{0}$, por lo que ${\vec {v}}_{20}^{\,G}={\vec {0}}$.

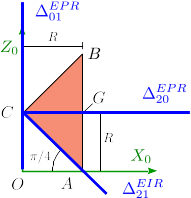
Ejes de los movimientos

La figura de la derecha muestra la localización de los ejes. Son Como ${\vec {v}}_{01}^{\,O}={\vec {0}}$ y ${\vec {\omega }}_{01}=\Omega \,{\vec {\omega }}_{01}$, el eje del movimiento {01} es $\Delta _{01}^{EPR}\equiv OZ_{1}$. Es un eje permanente de rotación.

Como ${\vec {v}}_{21}^{\,A}={\vec {v}}_{21}^{\,A}={\vec {0}}$ tenemos $\Delta _{21}^{EIR}\equiv CA$. Es un eje instantáneo de rotación.

Por último, con la composición {21}={20} + {01}. Aplicándola en $C$ tenemos

${\vec {v}}_{21}^{\,C}={\vec {v}}_{20}^{\,C}+{\vec {v}}_{01}^{\,C}\Longrightarrow {\vec {v}}_{20}^{\,C}={\vec {v}}_{21}^{\,C}-{\vec {v}}_{01}^{\,C}={\vec {0}}$

Además, ${\vec {v}}_{20}^{\,G}$, por lo que el eje del movimiento {20} es $\Delta _{20}^{EPR}$ es un eje permanente de rotación.

Reducciones cinemáticas

Movimiento {01} En el análisis previo ya hemos obtenido la reducción cinemática de este movimiento

${\vec {\omega }}_{01}=\Omega \,{\vec {k}}_{0,1},\qquad {\vec {v}}_{01}^{\,O}={\vec {0}}.$

Movimiento {20} Del análisis de los ejes tenemos

${\vec {\omega }}_{20}=\omega _{20}\,{\vec {\imath }}_{0},\qquad {\vec {v}}_{20}^{\,G}={\vec {0}}.$

Movimiento {21} Usando la composición {21} = {20} + {01} obtenemos

${\begin{array}{l}{\vec {\omega }}_{21}={\vec {\omega }}_{20}+{\vec {\omega }}_{01}=\omega _{20}\,{\vec {\imath }}_{0}+\Omega \,{\vec {k}}_{0}.\\\\{\vec {v}}_{21}^{\,G}={\vec {v}}_{20}^{\,G}+{\vec {v}}_{01}^{\,G}={\vec {v}}_{01}^{\,G}\end{array}}$

Para calcular esta velocidad usamos la ecuación del campo de velocidades del movimiento {01}

${\vec {v}}_{01}^{\,G}={\vec {v}}_{01}^{\,O}+{\vec {\omega }}_{01}\times {\overrightarrow {OG}}=(\Omega \,{\vec {k}}_{0})\times (R\,{\vec {\imath }}_{0}+R\,{\vec {k}}_{0})=R\Omega \,{\vec {\jmath }}_{0}.$

Por otro lado sabemos que ${\vec {v}}_{21}^{\,A}={\vec {0}}$. Usando la ecuación del campo de velocidades del movimiento {21} obtenemos

${\vec {v}}_{21}^{\,G}={\vec {v}}_{21}^{\,A}+{\vec {\omega }}_{21}\times {\overrightarrow {AG}}=(\omega _{20}\,{\vec {\imath }}_{0})\times (R\,{\vec {k}}_{0})=-R\omega _{20}\,{\vec {\jmath }}_{0}.$

Comparando los dos valores obtenemos $\omega _{20}=-\Omega$.

Con esto tenemos las tres reducciones cinemáticas

${\begin{array}{ll}{\vec {\omega }}_{01}=\Omega \,{\vec {k}}_{0},&{\vec {v}}_{01}^{\,G}=R\Omega \,{\vec {\jmath }}_{0},\\\\{\vec {\omega }}_{20}=-\Omega \,{\vec {\imath }}_{0},&{\vec {v}}_{20}^{\,G}={\vec {0}},\\\\{\vec {\omega }}_{21}=\Omega \,(-{\vec {\imath }}_{0}+{\vec {k}}_{0}),&{\vec {v}}_{21}^{\,G}=R\Omega \,{\vec {\jmath }}_{0}.\end{array}}$

Derivadas temporales de la reducciones cinemáticas

Movimiento {01}: al ser una rotación de eje permanente tenemos

${\begin{array}{l}{\vec {\alpha }}_{01}=\left.{\dfrac {\mathrm {d} {\vec {\omega }}_{01}}{\mathrm {d} t}}\right|_{1}={\vec {0}},\\\\{\vec {a}}_{01}^{\,O}=\left.{\dfrac {\mathrm {d} {\vec {v}}_{01}^{\,O}}{\mathrm {d} t}}\right|_{1}={\vec {0}}.\end{array}}$

Usamos la ecuación del campo de aceleraciones del movimiento {01} para calcular la aceleración en $G$

${\vec {a}}_{01}^{\,G}={\vec {a}}_{01}^{\,O}+{\vec {\alpha }}_{01}\times {\overrightarrow {OG}}+{\vec {\omega }}_{01}\times ({\vec {\omega }}_{01}\times {\overrightarrow {OG}})=-R\Omega ^{2}{\vec {\imath }}_{0}.$

Movimiento {20}: también es una rotación de eje permanente, por lo que

${\begin{array}{l}{\vec {\alpha }}_{20}=\left.{\dfrac {\mathrm {d} {\vec {\omega }}_{20}}{\mathrm {d} t}}\right|_{0}={\vec {0}},\\\\{\vec {a}}_{20}^{\,G}=\left.{\dfrac {\mathrm {d} {\vec {v}}_{20}^{\,G}}{\mathrm {d} t}}\right|_{0}={\vec {0}}.\end{array}}$

Movimiento {21} Utilizamos las leyes de composición

${\begin{array}{l}{\vec {\alpha }}_{21}={\vec {\alpha }}_{20}+{\vec {\alpha }}_{01}+{\vec {\omega }}_{01}\times {\vec {\omega }}_{20}=-\Omega ^{2}\,{\vec {\jmath }}_{0},\\\\{\vec {a}}_{21}^{\,G}={\vec {a}}_{20}^{\,G}+{\vec {a}}_{01}^{\,G}+2{\vec {\omega }}_{01}\times {\vec {v}}_{20}^{\,G}=-R\Omega ^{2}\,{\vec {\imath }}_{0}.\end{array}}$