Enunciado
Se tiene un sistema articulado formado por dos barras de la misma masa y la misma longitud b situadas sobre una superficie horizontal. La primera barra (“sólido 2”) tiene un extremo O fijo, de forma que gira alrededor de él formando un ángulo φ(t) respecto a un sistema de ejes fijos  . La segunda barra (“sólido 3”) está articulada en el extremo A de la primera de manera que forma un ángulo θ(t) con la prolongación del sólido 0. En función de θ, φ y sus derivadas y con ayuda de un sistema
. La segunda barra (“sólido 3”) está articulada en el extremo A de la primera de manera que forma un ángulo θ(t) con la prolongación del sólido 0. En función de θ, φ y sus derivadas y con ayuda de un sistema  ligado a la primera barra…
ligado a la primera barra…
- Calcule la velocidad del punto de articulación A y del extremo libre B de la segunda barra respecto al sistema fijo “1”.
- Localice la posición del centro instantáneo de rotación
 del movimiento de la segunda barra respecto a los ejes fijos.
del movimiento de la segunda barra respecto a los ejes fijos.
- Halle la aceleración del extremo B y del centro G del sólido 3 respecto al sistema fijo.
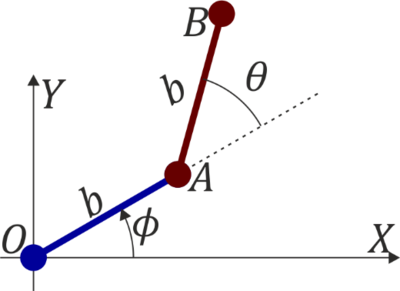
Sistemas de referencia
Emplearemos tres sistemas de referencia:
- El sistema fijo 1, que consideramos inmóvil.
- El sistema 2, ligado a la primera varilla, con el mismo origen, y tal que el eje
 está alineado con ella. Cuando
está alineado con ella. Cuando  , este eje es coincidente con el
, este eje es coincidente con el  . La relación de la base de este sistema con la del sistema 1 la da una rotación de un ángulo
. La relación de la base de este sistema con la del sistema 1 la da una rotación de un ángulo  :
:

- En este sistema, la posición del extremo A respoecto al origen es

- y la velocidad angular de este sólido

- usamos cantidades escalares porque al tratarse de un problema plano todas las velocidades angulares tienen la misma dirección (el sentido lo da el signo).
- Un sistema 3, ligado a la segunda varilla, con el eje
 a lo largo de ella. Cuando
a lo largo de ella. Cuando  , coincide con
, coincide con  . La relación de la base de este sistema con la del sistema 2 la da una rotación de un ángulo θ:
. La relación de la base de este sistema con la del sistema 2 la da una rotación de un ángulo θ:

- La posición del extremo B respecto a A es

- La velocidad angular de la varilla 3 respecto a la 2 es

- y respecto al sistema fijo

Velocidades
De A
La velocidad de A es simplemente la de una rotación en torno a O

De B
La velocidad de B la obtenemos mediante el campo de velocidades

El punto A, por ser una articulación entre “2” y “3”, tiene la misma velocidad en ambos sólidos respecto al “1”

y, por tanto, la velocidad de B es

Si queremos expresar esta velocidad empleando exclusivamente la base “2” simplemente desarrollamos el último vector

Centros instantáneos de rotación
Del movimiento {21}
Este es simplemente el punto O, alrededor del cual gira la barra OA.
Del movimiento {32}
Este es A, alrededor del cual gira la barra AB en este movimiento.
Del movimiento {31}
Este debe estar alineado con los dos anteriores. Obtenemos su posición a partir de la velocidad de A

y, respecto al origen de coordenadas

Este centro se encuentra efectivamente alineado con los otros dos, al hallarse sobre la recta OA. Dependiendo de los signos de las velocidades angulares, puede estar entre O y A, fuera del segmento o incluso en el infinito (caso de una traslación si  ).
).
Aceleraciones
La aceleración de B la calculamos hallando primero la de A


y a continuación la de B

El escribir este resultado en una sola base complica notablemente la expresión.
La aceleración de G, el punto medio de A y B, es




























