Calculo gráfico de velocidad media (GIOI)

Enunciado

La velocidad de una partícula en un movimiento rectilíneo sigue aproximadamente la gráfica de la figura cuando se representa frente al tiempo.

1. ¿Cuánto vale aproximadamente la velocidad media entre $t=0\,\mathrm {s}$ y $t=12\,\mathrm {s}$?
2. ¿Cuánto vale la distancia total recorrida por la partícula en el mismo intervalo?

Velocidad media

la velocidad media es igual al desplazamiento neto en el intervalo dividida por la duración de éste

$v_{m}={\frac {\Delta x}{\Delta t}}$

siendo el desplazamiento neto la suma de los desplazamientos infinitesimales

$\Delta x=\int _{0}^{\Delta t}v\,\mathrm {d} t$

Esta integral se puede hallar gráficamente. Es igual al área de la figura delimitada por la curva y el eje de abscisas, teniendo cuidado de que las partes que queden por debajo del eje contribuyen negativamente, ya que corresponden a un periodo en el cual la partícula está retrocediendo.

$\Delta x=\int _{0}^{\Delta t}v\,\mathrm {d} t=S_{1}-S_{2}$

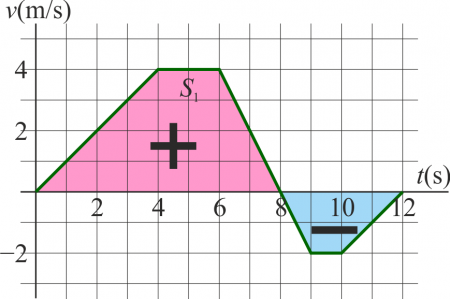
Cada una de las figuras es un trapecio, cuya área es igual a la semisuma de sus bases multiplicada por la altura. también puede hallarse como suma de triángulos y rectángulos

$S_{1}={\frac {(B+b)}{2}}h=\left({\frac {8\,\mathrm {s} +2\,\mathrm {s} }{2}}\right)\left(4\,{\frac {\mathrm {m} }{\mathrm {s} }}\right)=20\,\mathrm {m}$    $S_{2}={\frac {(B+b)}{2}}h=\left({\frac {4\,\mathrm {s} +1\,\mathrm {s} }{2}}\right)\left(2\,{\frac {\mathrm {m} }{\mathrm {s} }}\right)=5\,\mathrm {m}$

con lo que el desplazamiento neto es

$\Delta x=S_{1}-S_{2}=20\,\mathrm {m} -5\,\mathrm {m} =15\,\mathrm {m}$

y resulta la velocidad media

$v_{m}={\frac {15\,\mathrm {m} }{12\,\mathrm {s} }}=1.25\,{\frac {\mathrm {m} }{\mathrm {s} }}$

Desde el punto de vista cinemático, lo que ocurre es:

Entre t=0 s y t=4 s

La partícula se aleja con aceleración uniforme pasando su velocidad de 0 a 4m/s. En este tiempo recorre una distancia (4m/s)×4s/2 = 8m.

Entre t=4 s y t=6 s

Se sigue alejando, pero ahora a velocidad constante de 4m/s durante 2s, en los que recorre otros 8m.

Entre t=6 s y t=8 s

Sigue alejándose (la velocidad aun es positiva) durante 2s, pero con aceleración constante negativa, hasta que su velocidad llega a anularse. En este tiempo recorre (4m/s)×2s/2 = 4m.

En total, a partícula llega a alejarse 8+8+4 = 20m del origen.

Entre t=8 s y t=9 s

La velocidad es negativa, por lo que partícula comienza a acercarse aceleradamente al origen, con un desplazamiento de (−2m/s)×1s/2 = −1m.

Entre t=9 s y t=10 s

Se acerca al origen con velocidad constante de −2m/s durante 1s, siendo el desplazamiento −2m

Entre t=10 s y t=12 s

Sigue acercándose, pero ahora con aceleración constante positiva, con lo que se está frenando, hasta llegar a pararse. El desplazamiento en este intervalo es (−2m/s)×2s/2 = 2m

En total, desde el punto más alejado se acerca 5m.

El desplazamiento neto es entonces 20m−5m = 15 m. La velocidad media será 15m/12s = 1.25m/s

Distancia total

La distancia total recorrida no es igual al desplazamiento neto, ya que contribuyen positivamente todos los desplazamientos, sean de avance o de retroceso

$\Delta s=\int _{0}^{\Delta t}|v|\,\mathrm {d} t$

Gráficamente, esto equivale a contar todas las áreas como positivas

$\Delta s=S_{1}+S_{2}=20\,\mathrm {m} +5\,\mathrm {m} =25\,\mathrm {m}$

Cinemáticamente, la distancia total recorrida incluye tanto los 20m que se aleja como los 5 que se acerca, lo que da un total de 25m.