CIR de una bicicleta (G.I.A.)

Enunciado

Los radios de las ruedas delantera (sólido "2") y trasera (sólido "0") de un velocípedo son $R$ y $r$, respectivamente ($R>r$); y los puntos de contacto de aquéllas con el suelo (sólido "1") están separados una distancia $d$. Determinar gráficamente la posición del C.I.R. del movimiento {20}, sabiendo que las dos ruedas del velocípedo ruedan sin deslizar sobre el suelo.

Solución

Vamos a usar el teorema de los tres centros para encontrar el punto $I_{20}$. Para ello buscamos el CIR de cada uno de los movimientos del sistema

Movimiento {21}

La rueda gira sin deslizar, por tanto el punto de contacto es el punto $I_{21}$.

Movimiento {01}

La rueda gira sin deslizar, por tanto el punto de contacto es el punto $I_{01}$.

Movimiento {23}

Respecto al velocípedo, la rueda gira alrededor de su centro, que resulta ser el punto $I_{23}$.

Movimiento {03}

Respecto al velocípedo, la rueda gira alrededor de su centro, que resulta ser el punto $I_{03}$.

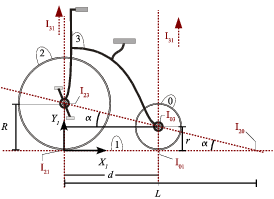
Movimiento {20}

De la composición {20}={21}+{10}, el CIR $I_{20}$ debe estar en la línea que une $I_{21}$ e $I_{01}$. Y de la composición {20}={23}+{30}, el CIR $I_{20}$ debe estar en la línea que une $I_{23}$ e $I_{03}$. El punto de corte de estas dos líneas determina la posición de $I_{20}$. De la figura vemos que

$\tan \alpha ={\dfrac {R-r}{d}}={\dfrac {R}{L}}\Rightarrow L={\dfrac {R}{\tan \alpha }}={\dfrac {R\,d}{R-r}}$

Si consideramos el origen del triedro "1" en $I_{21}$, el vector de posición de $I_{20}$ es

${\overrightarrow {I_{21}I_{20}}}={\dfrac {R\,d}{R-r}}\,{\vec {\imath }}_{1}$

Observemos que al generalizar el concepto de CIR a una traslación colocando el CIR en el infinito, podemos incluir las traslaciones en el teorema de los tres centros. En la figura puede observarse como $I_{01}$, $I_{03}$ e $I_{31}$ están alineados, así como $I_{21}$, $I_{23}$ e $I_{31}$.