Bloque sobre plano inclinado girando

Enunciado

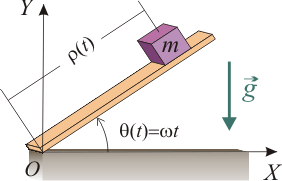
Una partícula puntual de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} se mueve sobre un plano inclinado. A su vez, el plano gira de modo que el ángulo con la horizontal es $\theta (t)=\omega t$. Sobre la masa actúa además la gravedad ${\vec {g}}$. El contacto entre la partícula y el plano es liso.

1. Encuentra la expresión de la ecuación diferencial que cumple la distancia de la partícula al origen de coordenadas, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho(t)} , así como la expresión que da el valor de la fuerza de reacción vincular ${\vec {\Phi }}(t)$.
2. Demuestra que, para los valores apropiados de las constantes $\alpha$ y $K$, la expresión siguiente es solución de la ecuación diferencial. ¿Cuáles son esos valores de $\alpha$ y $K$? $\rho (t)=A\,\cosh(\alpha t)+B\,\mathrm {senh} \,(\alpha t)+K\,\mathrm {sen} \,(\omega t)$
3. Si en el instante inicial tenemos $\rho (0)=0$ y ${\dot {\rho }}(0)=v_{0}$ encuentra cuánto valen las constantes $A$ y $B$ de la expresión anterior.
4. ¿Se conserva la energía mecánica del sistema? Razona la respuesta.

Solución

Ecuación diferencial y fuerza de reacción vincular

Este problema es similar a uno hecho en clase por dos métodos distintos. Se trata de describir el movimiento de una partícula puntual sobre un plano inclinado que a su vez rota con velocidad angular uniforme Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega } . Hay tres formas distintas de encontrar la ecuación diferencial y la expresión de la fuerza de reacción vincular, a saber: usando coordenadas polares, coordenadas cartesianas o dinámica en sistemas de referencia no inerciales.

Coordenadas polares

En Dinámica de un partícula, la ecuación diferencial que determina el movimiento es la Segunda Ley de Newton

$m\,{\vec {a}}=\sum _{i}{\vec {F}}_{i}$

donde $m$ es la masa de la partícula, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{a} } su aceleración y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_i } las fuerzas que actúan sobre ella. Vamos a resolverlo usando ecuaciones polares. Al final del problema explicaremos como se resuelve con los otros dos métodos. figura vemos que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} m\,\vec{g} = -m\,g\,\mathrm{sen}(\theta)\,\vec{u}_{\rho} - m\,g\cos(\theta)\,\vec{u}_{\theta} \\ \\ \vec{\Phi} = \Phi\,\vec{u}_{\theta} \end{array} }

Según el enunciado del problema, el plano gira con velocidad angular constante, de modo que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta=\omega t } .

Aceleración de la partícula

En coordenadas polares los vectores de posición, velocidad y aceleración de un punto material son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{r}(t) = \rho(t)\,\vec{u}_{\rho}(t) \\ \\ \vec{v}(t) = \dot{\vec{r}} = \dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta} \\ \\ \vec{a}(t) = \dot{\vec{v}} = (\ddot{\rho}-\rho\,\dot{\theta}^2)\,\vec{u}_{\rho} + (2\dot{\rho}\,\dot{\theta} + \rho\,\ddot{\theta})\,\vec{u}_{\theta} \end{array} }

En este problema tenemos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}=\omega } y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot{\theta}=0 } . Por tanto la aceleración es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{a} = (\ddot{\rho} - \rho\,\omega^2)\,\vec{u}_{\rho} + 2\,\omega\,\dot{\rho}\,\vec{u}_{\theta} }

Ecuación diferencial

Ahora podemos escribir la Segunda Ley de Newton proyectada en el sistema de coordenadas cartesianas

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m\,\vec{a} = m\,\vec{g} + \vec{\Phi} \Rightarrow \left\{ \begin{array}{lcl} \vec{u}_{\rho} & \to & m\,(\ddot{\rho} - \rho\,\omega^2) = -m\,g\,\mathrm{sen}(\omega t)\\ & & \\ \vec{u}_{\theta} & \to & 2\,m\,\omega\,\dot{\rho} = - m\,g\cos(\omega t) + \Phi \end{array} \right. }

Así pues, la ecuación diferencial es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot{\rho} = \omega^2\,\rho - g\,\mathrm{sen}(\omega t) }

y la expresión que da la fuerza de reacción vincular

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Phi = 2\,m\,\omega\,\dot{\rho} + m\,g\cos(\omega t) }

Verificación de la solución del enunciado

Se nos pide ahora que verifiquemos que la función

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho(t) = A\,\cosh(\alpha t) + B\,\mathrm{senh}\,(\alpha t) + K\,\mathrm{sen}\,(\omega t) }

es solución de la ecuación diferencial con los valores adecuados de las constantes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \alpha } y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle K } . Calculamos cada lado de la ecuación diferencial. La derivada de la solución aportada es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\rho} = A\,\alpha\,\mathrm{senh}(\alpha t) + B\,\alpha\cosh(\alpha t) + K\,\omega\cos(\omega t) }

El lado izquierdo de la ecuación diferencial es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \ddot{\rho} = A\,\alpha^2\cosh(\alpha t) + B\,\alpha^2\,\mathrm{senh}(\alpha t) - K\,\omega^2\,\mathrm{sen}(\omega t) }

El lado derecho es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \omega^2\,\rho - g\,\mathrm{sen}(\omega t) = A\,\omega^2\cosh(\alpha t) + B\,\omega^2\,\mathrm{senh}(\alpha t) + (K\,\omega^2 - g)\,\mathrm{sen}(\omega t) }

Para que el lado izquierdo y el derecho coincidan en todo instante Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle t} debe ocurrir

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \alpha^2 = \omega^2 \qquad \qquad -\omega^2 K = \omega^2 K -g }

Es decir, la función propuesta es solución si

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \alpha = \omega\qquad \qquad K = \dfrac{g}{2\omega^2} }

Condiciones iniciales

Podemos calcular las constantes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A } y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B } cuando conocemos las condiciones iniciales. Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \rho(t) = A\cosh(\alpha t) + B\,\mathrm{senh}(\alpha t) + K\,\mathrm{sen}(\omega t) \\ \\ \dot{\rho} = A\,\alpha\,\mathrm{senh}(\alpha t) + B\,\alpha\,\cosh(\alpha t) + K\,\omega\cos(\omega t) \end{array} }

Para aplicar las condiciones iniciales tenemos en cuenta que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \cos(0) = 1 \qquad\qquad \mathrm{sen}(0)=0 \qquad\qquad \cosh(0)=1 \qquad\qquad \mathrm{senh}(0) = 0 }

Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{lcl} \rho(0) = 0 & \to & A = 0 \\ & & \\ \dot{\rho}(0) = v_0 & \to & B\,\alpha + K\,\omega = v_0 \end{array} }

Sustituyendo los valores de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \alpha } y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B } del apartado anterior tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A=0 \qquad \qquad B = \dfrac{v_0}{\omega} - \dfrac{g}{2\omega^2} }

Conservación de la energía mecánica

En este sistema no se conserva la energía mecánica. Aunque no hay rozamiento, la fuerza de reacción vincular realiza trabajo sobre la partícula, y esta fuerza de reacción vincular no es conservativa. Podemos calcular la potencia que la fuerza de reacción vincular transfiere a la partícula

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle P_{\Phi} = \vec{\Phi}\cdot\vec{v} = (\Phi\,\vec{u}_{\theta})\cdot(\dot{\rho}\,\vec{u}_{\rho} + \rho\,\omega\,\vec{u}_{\theta}) = \rho\,\omega\,\Phi\neq0 }

Al ser distinta de cero, es una fuerza no conservativa que realiza trabajo, por lo que la energía mecánica no se conserva. La fuente de esta potencia es el motor que está haciendo girar el plano.

Resolución con sistemas de referencia no inerciales

Otra forma de encontrar la ecuación diferencial y la expresión de la fuerza de reacción vincular es aplicar la Segunda Ley de Newton en un triedro que gire solidariamente con el plano (sólido "0"). Dado que es un sistema de referencia no inercial hay que corregir la Segunda Ley introduciendo las fuerzas de inercia

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m\,\vec{a}\,^P_{20} = m\,\vec{g} + \vec{\Phi} + \vec{F}_{\mathrm{arr}} + \vec{F}_{\mathrm{cor}} }

Veamos cada uno de los términos de esta ecuación.

En el término de la izquierda, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{a}\,^P_{20} } representa la aceleración de la partícula respecto del plano. Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{r}\,^P_{20} = \rho\,\vec{\imath}_0 \\ \\ \vec{v}\,^P_{20} = \dot{\rho}\,\vec{\imath}_0 \\ \\ \vec{a}\,^P_{20} = \ddot{\rho}\,\vec{\imath}_0 \\ \\ \end{array} }

El peso en el triedro "0" es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m\,\vec{g} = -m\,g\,\mathrm{sen}\theta\,\vec{\imath}_0 - m\,g\cos\theta\,\vec{\jmath}_0 }

La fuerza de reacción vincular es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\Phi} = \Phi\,\vec{\jmath}_0 }

La fuerza de arrastre se expresa

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_{\mathrm{arr}} = -m\,\vec{a}\,^P_{01} }

El origen del triedro, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O } es un punto fijo, y la aceleración angular del movimiento {01} es nula. Por tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \,\vec{a}\,^P_{01} = \,\vec{a}\,^O_{01} + \vec{\alpha}_{01}\times\overrightarrow{OP} - |\vec{\omega}_{01}|^2\overrightarrow{OP} = -\omega^2\,\rho\,\vec{\imath}_0 }

Con lo que la fuerza de arrastre es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_{\mathrm{arr}} = m\,\omega^2\,\rho\,\vec{\imath}_0 }

Por último, la fuerza de Coriolis es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_{\mathrm{cor}} = -2\,m\,\vec{\omega}_{01}\times\vec{v}\,^P_{20} = -2\,m\,\omega\,\dot{\rho}\,\vec{\jmath}_0 }

Escribimos la Segunda Ley de Newton para sistemas de referencia no inerciales proyectada en el triedro "0"

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m\,\vec{a}\,^P_{20} = m\,\vec{g} + \vec{\Phi} + \vec{F}_{\mathrm{arr}} + \vec{F}_{\mathrm{cor}} = \left\{ \begin{array}{lcl} \vec{\imath}_0 & \to & \ddot{\rho} = \omega^2\rho - g\,\mathrm{sen}(\omega t)\\ &&\\ \vec{\jmath}_0 & \to & \Phi = m\,g\cos(\omega t) + 2\,m\,\omega\,\dot{\rho} \end{array} \right. }

Obtenemos las mismas expresiones que en el primer apartado.

Resolución usando coordenadas cartesianas

Por último vamos a resolver el problema usando coordenadas cartesianas. Usamos el triedro "1", que es inercial. La Segunda Ley de Newton en este triedro es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m\,\vec{a}\,^P_{21} = m\,\vec{g} + \vec{\Phi} }

Proyectando en el triedro "1" tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{r}\,^P_{21} = \rho(t)\cos(\omega t)\,\vec{\imath}_1 + \rho(t)\,\mathrm{sen}(\omega t)\,\vec{\jmath}_1 \\ \\ \vec{v}\,^P_{21} = (\dot{\rho}\cos(\omega t) - \rho\,\omega\,\mathrm{sen}(\omega t))\,\vec{\imath}_1 + (\dot{\rho}\,\mathrm{sen}(\omega t) + \rho\,\omega\cos(\omega t))\,\vec{\jmath}_1 \\ \\ \vec{a}\,^P_{21} = ( (\ddot{\rho}-\rho\,\omega^2)\cos(\omega t) - 2 \omega\,\dot{\rho}\,\mathrm{sen}(\omega t))\,\vec{\imath}_1 + ( (\ddot{\rho}-\rho\,\omega^2)\mathrm{sen}(\omega t) + 2 \omega\,\dot{\rho}\cos(\omega t))\,\vec{\jmath}_1 \end{array} }

El peso en este triedro es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m\,vec{g} = -m\,g\,\vec{\jmath}_1 }

y la fuerza de reacción vincular es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\Phi} = -\Phi\,\mathrm{sen}(\omega t)\,\vec{\imath}_1 + \Phi\,\cos(\omega t)\,\vec{\jmath}_1 }

Igualando las componentes en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\imath}_1 } y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\jmath}_1 } obtenemos dos ecuaciones escalares.

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} m(\ddot{\rho}-\rho\,\omega^2)\cos^2\theta - 2\,m\,\dot{\rho}\,\omega\,\mathrm{sen}\theta = -\Phi\,\mathrm{sen}\theta\\ \\ m(\ddot{\rho}-\rho\,\omega^2)\,\mathrm{sen}^2\theta + 2\,m\,\dot{\rho}\,\omega\cos\theta = \Phi\cos\theta - m\,g \end{array} }

Pasando el término Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle - m\,g } del segundo miembro de la segunda ecuación a la izquierda, dividimos una por otra para eliminar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Phi } . Multiplicando en aspa la expresión que queda reobtenemos la ecuación diferencial para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho(t) } . Después despejamos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \Phi(t) } de una de las dos ecuaciones.

Como se puede ver, este método es el más complicado de los tres.