Barra oscilando respecto a uno de sus extremos (GIC)

Enunciado

Una barra homogénea de longitud $L$ y masa $M$ cuelga por uno de sus extremos de modo que se encuentra en equilibio en posición vertical. Analiza el movimiento de la barra si se separa de la vertical un ángulo $\theta _{0}$ pequeño.

Solución

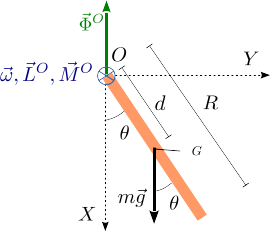
La figura muestra la barra colgando del punto $O$. En un péndulo ideal se puede considerar que la masa está concentrada en un extremo, pero aquí eso no es posible. Hay que tratar toda la barra como un sólido rígido. Este tipo de sistema se llaman péndulos físicos o compuestos.

La barra realiza un movimiento de rotación respecto al eje $OZ$. Para describir este movimiento vamos a usar un vector rotación ${\vec {\omega }}=\omega \,vec{k}$ y el momento angular de la barra respecto al punto $O$, ${\vec {L}}^{O}$. Como el eje de rotación es fijo, estas dos magnitudes están relacionadas

${\vec {L}}^{O}=I{\vec {\omega }}$

donde $I$ es el momento de inercia de la barra respecto al eje $OZ$.

La ecuación de movimiento se obtiene de aplicar la "Segunda Ley de Newton para la rotación"

${\dfrac {\mathrm {d} {\vec {L}}^{O}}{\mathrm {d} t}}={\vec {M}}^{O}$

siendo ${\vec {M}}^{O}$ el momento neto de las fuerzas que actúan sobre la barra. En este caso esas fuerzas son el peso, aplicado en el centro de masas de la barra, $G$, y la fuerza de reacción vincular en $O$, que sujeta a la barra. El momento de esta fuerza de reacción vincular respecto a $O$. La única fuerza que ejerce momento es el peso

${\vec {M}}^{O}={\overrightarrow {OG}}\times (m{\vec {g}})=\left(d\cos \theta \,{\vec {\imath }}+d\,\mathrm {sen} \,\theta \,{\vec {\jmath }}\right)\times (-mg{\vec {\imath }})=-mgd\,\mathrm {sen} \,\theta \,{\vec {k}}$

El valor $d$ es la distancia del punto $O$ al centro de masas $G$. En este caso es la mitad de la longitud de la barra, $d=R/2$, por lo que

${\vec {M}}^{O}=-{\dfrac {1}{2}}mgR\,\mathrm {sen} \,\theta \,{\vec {k}}$

Por otro lado, la derivada temporal del momento cinético es

${\dfrac {\mathrm {d} {\vec {L}}^{O}}{\mathrm {d} t}}=I{\dot {\vec {\omega }}}=I{\ddot {\theta }}\,{\vec {k}}$

Igualando las dos expresiones obtenemos

${\ddot {\theta }}=-{\dfrac {mgR}{2I}}\,\mathrm {sen} \,\theta$

Esta es la ecuación diferencial para $\theta (t)$. No sabemos resolver esta ecuación, pero si el ángulo de oscilación es pequeño podemos hacer la aproximación $\mathrm {sen} \,\theta \approx \theta$, y la ecuación queda

${\ddot {\theta }}=-{\dfrac {mgR}{2I}}\,\theta$

Esta es la ecuación de un oscilador armónico con frecuencia angular

$\omega ={\sqrt {\dfrac {mgR}{2I}}}$

Es decir, si el ángulo con la vertical es pequeño, la barra oscila con un período

$T={\dfrac {2\pi }{\omega }}=2\pi {\sqrt {\dfrac {2I}{mgR}}}$

El momento de inercia de una barra respecto de un eje perpendicular a ella que pasa por su extremo es

$I={\dfrac {1}{3}}mR^{2}$

con lo que el período de oscilación es

$T=2\pi {\sqrt {\dfrac {2R}{3g}}}$

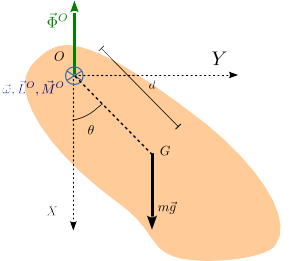
Hay que destacar que, hasta que hemos sustituido el momento de inercia concreto para la barra, el tratamiento es válido para un cuerpo de forma general, por ejemplo el de la figura de la derecha. Lo único que hay que cambiar es dejar el resultado en función de la distancia entre el punto $O$ y el centro de masas del cuerpo, $d$. Así pues, si el ángulo $\theta$ es pequeño, este cuerpo realizará oscilaciones periódicas con período

$T=2\pi {\sqrt {\dfrac {I}{mgd}}}$

En particular podemos recuperar el resultado para un péndulo ideal de longitud $d$. En este caso la masa está concentrada en el extremo de la cuerda, por lo que el momento de inercia es $I=md^{2}$. Sustituyendo en la expresión del período recuperamos el período de un péndulo ideal.