Barra girando alrededor de otra barra horizontal (Sep. 2018 G.I.C.)

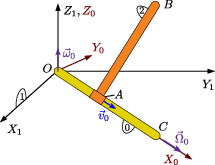
Enunciado

Una barra de longitud $L$ (sólido "0") puede rotar alrededor del eje $OZ_{1}$ con velocidad angular constante ${\vec {\omega }}_{0}$, como se indica en la figura. El punto $O$ de la barra es fijo. La barra "0" siempre está contenida en el plano $OX_{1}Y_{1}$. Otra barra, también de longitud $L$ (sólido "2"), está conectada a la barra "0" por un pasador en el punto $A$. El pasador desliza sobre la barra "0" con velocidad constante $v_{0}$. Además, la barra "2" gira alrededor de la barra "0" con velocidad angular uniforme ${\vec {\Omega }}_{0}$. En $t=0$ la barra "0" estaba sobre el eje $OX_{1}+$, el extremo $A$ de la barra "2" estaba en el punto $O$ y el punto $B$ estaba en el plano $OX_{1}Y_{1}$. Los vectores ${\vec {v}}_{0}$, ${\vec {\omega }}_{0}$ y ${\vec {\Omega }}_{0}$ apuntan en el sentido indicado en la figura.

1. Determina las reducciones cinemáticas $\{01\},\{20\},\{21\}$.
2. Calcula las derivadas temporales de las reducciones cinemáticas del apartado anterior.
3. ¿Qué tipo de movimiento es cada uno de ellos?
4. Sea $t_{1}$ el instante de tiempo para el cual $B$ está en el punto más alto de su trayectoria. Calcula ${\vec {v}}_{21}^{B}$ y ${\vec {a}}_{21}^{B}$ en ese instante.

Solución

Reducciones cinemáticas

Para el movimiento {01} tenemos

${\vec {\omega }}_{01}=\omega _{0}\,{\vec {k}}_{0},\qquad {\vec {v}}_{01}^{O}={\vec {0}}.$

Para el movimiento {20} es

${\vec {\omega }}_{20}=\Omega _{0}\,{\vec {\imath }}_{0},\qquad {\vec {v}}_{20}^{A}=v_{0}\,{\vec {\imath }}_{0}.$

Para el movimiento {21} usamos las leyes de composición para {21} = {20} + {01}. Para el vector velocidad de rotación

${\begin{array}{l}{\vec {\omega }}_{21}={\vec {\omega }}_{20}+{\vec {\omega }}_{01}=\Omega _{0}\,{\vec {\imath }}_{0}+\omega _{0}\,{\vec {k}}_{0}.\end{array}}$

Reducimos la velocidad en $A$

${\begin{array}{ll}{\vec {v}}_{21}^{A}=&{\vec {v}}_{20}^{A}+{\vec {v}}_{01}^{A}=v_{0}\,{\vec {\imath }}_{0}+v_{0}\omega _{0}t\,{\vec {\jmath }}_{0}.\\&\\&{\vec {v}}_{20}^{A}=v_{0}{\vec {\imath }}_{0},\\&\\&{\vec {v}}_{01}^{A}={\vec {v}}_{01}^{O}+{\vec {\omega }}_{01}\times {\overrightarrow {OA}}=(\omega _{0}\,{\vec {k}}_{0})\times (v_{0}t\,{\vec {\imath }}_{0})=v_{0}\omega _{0}t\,{\vec {\jmath }}_{0}.\\\end{array}}$

Derivadas temporales de las reducciones cinemáticas

Para {01}

${\vec {\alpha }}_{01}=\left.{\dfrac {\mathrm {d} {\vec {\omega }}_{01}}{\mathrm {d} t}}\right|_{1}={\vec {0}},\qquad {\vec {a}}_{01}^{O}=\left.{\dfrac {\mathrm {d} {\vec {v}}_{01}^{O}}{\mathrm {d} t}}\right|_{1}={\vec {0}}.$

Para {20}

${\vec {\alpha }}_{20}=\left.{\dfrac {\mathrm {d} {\vec {\omega }}_{20}}{\mathrm {d} t}}\right|_{0}={\vec {0}},\qquad {\vec {a}}_{20}^{A}=\left.{\dfrac {\mathrm {d} {\vec {v}}_{20}^{A}}{\mathrm {d} t}}\right|_{0}={\vec {0}}.$

Para {21} usamos de nuevo las leyes de composición. Para la aceleración angular

${\begin{array}{l}{\vec {\alpha }}_{21}={\vec {\alpha }}_{20}+{\vec {\alpha }}_{01}+{\vec {\omega }}_{01}\times {\vec {\omega }}_{20}=\Omega _{0}\omega _{0}\,{\vec {\jmath }}_{0}.\end{array}}$

Para la aceleración en $A$

${\begin{array}{ll}{\vec {a}}_{21}^{A}=&{\vec {a}}_{20}^{A}+{\vec {a}}_{01}^{A}+2{\vec {\omega }}_{01}\times {\vec {v}}_{20}^{A}=-v_{0}\omega _{0}^{2}t\,{\vec {\imath }}_{0}+2v_{0}\omega _{0}\,{\vec {\jmath }}_{0}.\\&\\&{\vec {a}}_{01}^{A}={\vec {a}}_{01}^{O}+{\vec {\alpha }}_{01}\times {\overrightarrow {OA}}+{\vec {\omega }}_{01}\times ({\vec {\omega }}_{01}\times {\overrightarrow {OA}})=-v_{0}\omega _{0}^{2}t\,{\vec {\imath }}_{0}.\\&\\&{\vec {a}}_{20}^{A}={\vec {0}}.\\&\\&2{\vec {\omega }}_{01}\times {\vec {a}}_{20}^{A}=2v_{0}\omega _{0}\,{\vec {\jmath }}_{0}.\end{array}}$

Tipos de movimientos

Para el movimiento {01}:

${\vec {\omega }}_{01}\neq {\vec {0}}\qquad {\vec {v}}_{01}^{O}.$

Es una rotación pura de eje permanente. El eje es $\Delta _{01}^{EPR}\equiv OZ_{1}$.

Para el movimiento {20}:

${\vec {\omega }}_{20}\neq {\vec {0}}\qquad {\vec {v}}_{20}^{A}\cdot {\vec {\omega }}_{20}\neq 0.$

Es un movimiento helicoidal de eje permanente. El eje es $\Delta _{20}^{EPRMD}\equiv OX_{0}$. Siempre pasa por los mismos puntos del sólido "0" (la barra "0")

Para el movimiento {21}:

${\vec {\omega }}_{21}\neq {\vec {0}}\qquad {\vec {v}}_{21}^{A}\cdot {\vec {\omega }}_{20}\neq 0.$

Es un movimiento helicoidal de eje instantáneo. Para localizar el eje hacemos

${\overrightarrow {AI}}_{21}^{\,*}={\dfrac {{\vec {\omega }}_{21}\times {\vec {v}}_{21}^{\,A}}{|{\vec {\omega }}_{21}|^{2}}}={\dfrac {1}{\omega _{0}^{2}+\Omega _{0}^{2}}}\,(-\omega _{0}^{2}v_{0}t\,{\vec {\imath }}_{0}+\omega _{0}v_{0}\,{\vec {\jmath }}_{0}+\omega _{0}\Omega _{0}v_{0}t\,{\vec {k}}).$

Nota: En el examen no se pedían los ejes.

Velocidad y aceleración en $B$

En el instante $t_{1}$ tenemos

${\begin{array}{l}{\overrightarrow {OA}}=v_{0}t_{1}\,{\vec {\imath }}_{0},\\\\{\overrightarrow {AB}}=L\,{\vec {k}}_{0},\\\\{\overrightarrow {OB}}={\overrightarrow {OA}}+{\overrightarrow {AB}}=v_{0}t_{1}\,{\vec {\imath }}_{0}+L\,{\vec {\jmath }}_{0}.\end{array}}$

Para la velocidad

${\begin{array}{ll}{\vec {v}}_{21}^{B}=&{\vec {v}}_{20}^{B}+{\vec {v}}_{01}^{B}=v_{0}\,{\vec {\imath }}_{0}+(v_{0}\omega _{0}t_{1}-L\Omega _{0})\,{\vec {\jmath }}_{0}.\\&\\&{\vec {v}}_{20}^{B}={\vec {v}}_{20}^{A}+{\vec {\omega }}_{20}\times {\overrightarrow {AB}}=v_{0}\,{\vec {\imath }}_{0}-L\Omega _{0}\,{\vec {\jmath }}_{0},\\&\\&{\vec {v}}_{01}^{B}={\vec {v}}_{01}^{\,O}+{\vec {\omega }}_{01}\times {\overrightarrow {OB}}=\omega _{0}v_{0}t_{1}\,{\vec {\jmath }}_{0}.\end{array}}$

Para la aceleración en $B$

${\begin{array}{ll}{\vec {a}}_{21}^{B}=&{\vec {a}}_{20}^{B}+{\vec {a}}_{01}^{B}+2{\vec {\omega }}_{01}\times {\vec {v}}_{20}^{B}=(2L\omega _{0}\Omega _{0}-\omega _{0}^{2}v_{0}t_{1})\,{\vec {\imath }}_{0}+2v_{0}\omega _{0}\,{\vec {\jmath }}_{0}-L\Omega _{0}^{2}\,{\vec {k}}_{0}.\\&\\&{\vec {a}}_{20}^{B}={\vec {a}}_{20}^{A}+{\vec {\alpha }}_{20}\times {\overrightarrow {AB}}+{\vec {\omega }}_{20}\times ({\vec {\omega }}_{20}\times {\overrightarrow {AB}})=-L\Omega _{0}^{2}\,{\vec {k}}_{0},\\&\\&{\vec {a}}_{01}^{B}={\vec {a}}_{01}^{O}+{\vec {\alpha }}_{01}\times {\overrightarrow {OB}}+{\vec {\omega }}_{01}\times ({\vec {\omega }}_{01}\times {\overrightarrow {OB}})=-\omega _{0}^{2}v_{0}t_{1}\,{\vec {\imath }}_{0},\\&\\&2{\vec {\omega }}_{01}\times {\vec {a}}_{20}^{B}=2L\omega _{0}\Omega _{0}\,{\vec {\imath }}_{0}+2v_{0}\omega _{0}\,{\vec {\jmath }}_{0}.\end{array}}$