Barra girando, Enero 2014 (G.I.C.)

Enunciado

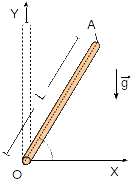
La barra de la figura puede girar sobre su extremo inferior $O$. La barra es homogénea, de lonigtud $L$ y masa $M$. En el instante inicial se encuentra en posición vertical $(\theta (0)=\pi /2)$. En ese instante empieza a moverse de modo que el extremo $A$ tiene una velocidad instantánea $v_{0}\,{\vec {\imath }}$.

1. Calcula la velocidad angular de la barra en el instante inicial.
2. Si $I$ es el momento de inercia de la barra respecto a un eje perpendicular al plano $OXY$ y que pasa por el punto $O$, encuentra la ecuación diferencial que describe el movimiento de la barra.
3. Encuentra la expresión que da la velocidad angular con la que gira la barra en función del ángulo $\theta$.

Solución

Velocidad angular inicial

El extremo $A$ de la barra realiza un movimiento circular con velocidad angular

$\omega ={\dot {\theta }}$

En el movimiento circular, la velocidad lineal y la velocidad angular están relacionadas. En módulo

$|v|=R|{\dot {\theta }}|$

siendo $R$ el radio de la circunferencia. En este caso el radio es $R=L$. La velocidad inicial tiene módulo $v_{0}$. Como se mueve hacia la derecha, el ángulo $\theta$ disminuye, es decir, la derivada ha de ser negativa. Por tanto, la velocidad angular inicial es

${\dot {\theta }}(0)=-{\dfrac {v_{0}}{L}}$

Ecuación de movimiento

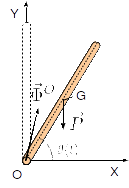
La barra es un sólido rígido que realiza un movimiento de rotación alrededor de un eje fijo. Describimos su movimiento utilizando su momento cinético respecto al eje de rotación (el eje $OZ$). Como el eje es fijo, el momento cinético puede escribirse como

${\vec {L}}_{O}=I\,{\vec {\omega }}=I\,{\dot {\theta }}\,{\vec {k}}$

donde $I$ es el momento de inercia de la barra respecto al eje $OZ$.

La variación en el tiempo del momento cinético viene dado por el momento resultante de las fuerzas que actúan sobre la barra respecto al punto $O$

${\dfrac {\mathrm {d} {\vec {L}}_{O}}{\mathrm {d} t}}={\vec {M}}_{O}$

Las fuerzas que actúan sobre la barra son su peso, aplicado en su centro de masas, y la reacción vincular en el punto $O$. Como se ve en la figura, sólo el peso ejerce momento respecto del punto $O$. Por tanto

${\vec {M}}_{O}={\overrightarrow {OG}}\times {\vec {P}}=\left({\dfrac {1}{2}}L\cos \theta \,{\vec {\imath }}+{\dfrac {1}{2}}\mathrm {sen} \,\theta \,{\vec {\jmath }}\right)\times \left(-Mg\,{\vec {\jmath }}\right)=-{\dfrac {MgL}{2}}\cos \theta \,{\vec {k}}$

La derivada del momento cinético puede escribirse

${\dfrac {\mathrm {d} {\vec {L}}_{O}}{\mathrm {d} t}}=I{\ddot {\theta }}\,{\vec {k}}$

Igualando al momento neto, y teniendo en cuenta que al ser los dos vectores colineales podemos trabajar con sus componentes, obtenemos la ecuación diferencial

${\ddot {\theta }}=-{\dfrac {MgL}{2I}}\cos \theta$

Las condiciones iniciales en este problema en concreto son

$\theta (0)=\pi /2,\qquad \qquad {\dot {\theta }}(0)=-v_{0}/L$

Velocidad angular en función del ángulo

La ecuación diferencial anterior es difícil de resolver. Pero podemos obtener la velocidad angular en función del ángulo con razonamientos energéticos. La única fuerza que realiza trabajo, el peso, es conservativa, por lo que se conserva la energía mecánica. Escogiendo como origen de energía potencial gravitatoria la altura $y=0$, la energía potencial gravitatoria de la barra viene dada por la altura de su centro de masas. En el instante inicial

$U_{g}(0)={\dfrac {1}{2}}MgL$

La energía cinética inicial es

$T(0)={\dfrac {1}{2}}I\omega ^{2}(0)={\dfrac {Iv_{0}^{2}}{2L^{2}}}$

Por tanto la energía mecánica es

$E=U_{g}(0)+T(0)={\dfrac {1}{2}}MgL+{\dfrac {Iv_{0}^{2}}{2L^{2}}}$

Para un ángulo cualquiera la energía potencial gravitatoria es

$U_{g}(\theta )={\dfrac {1}{2}}MgL\,\mathrm {sen} \,\theta$

y la energía cinética es

$T(\theta )={\dfrac {1}{2}}I\omega ^{2}(\theta )$

con lo que la energía mecánica es

$E={\dfrac {1}{2}}MgL\,\mathrm {sen} \,\theta +{\dfrac {1}{2}}I\omega ^{2}(\theta )$

Igualando las dos expresiones de energía mecánica y despejando la velocidad angular obtenemos

$\omega (\theta )={\sqrt {{\dfrac {v_{0}^{2}}{L^{2}}}+{\dfrac {MgL}{I}}\,(1-\mathrm {sen} \,\theta )}}$