Aceleración lineal con el tiempo (GIOI)

Enunciado

Una partícula de masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle m=2\,\mathrm{kg}} describe un movimiento rectilíneo en el que la aceleración, como función del tiempo sigue la gráfica de la figura. La partícula parte en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0\,\mathrm{s}} del reposo en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=0} .

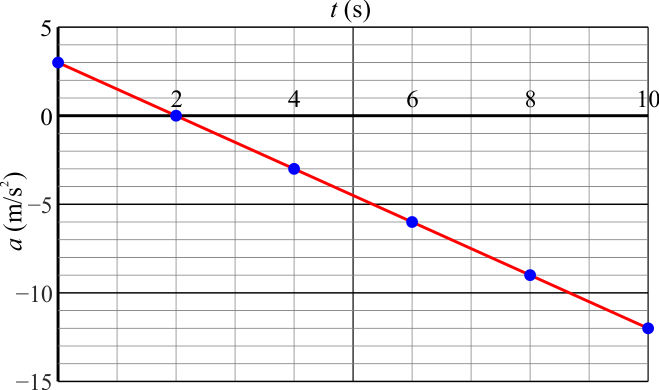
1. ¿Cuánto vale la rapidez de la partícula en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=10\,\mathrm{s}} ?
2. ¿Cuál es su velocidad media entre Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0\,\mathrm{s}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=10\,\mathrm{s}} ?
3. ¿Cuál es la distancia total recorrida entre Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0\,\mathrm{s}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=10\,\mathrm{s}} ?
4. ¿Cuánto vale la rapidez media en dicho intervalo?

Rapidez

Lo primero que debemos hacer es determinar la aceleración como función del tiempo, de ahí la velocidad y de ésta la posición.

La gráfica es la de una recta

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a=A+Bt\,}

que en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0\,\mathrm{s}} vale 3 m/s² y en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=2\,\mathrm{s}} vale 0. Sustituyendo estos dos valores hallamos A y B y resulta, en el SI

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a=3-\frac{3}{2}t}

Integrando esta aceleración obtenemos la velocidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v=v_0+\int_0^t a\,\mathrm{d}t=3t-\frac{3}{4}t^2}

La velocidad en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=10\,\mathrm{s}} es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v=\left(30-\frac{300}{4}\right)\,\frac{\mathrm{m}}{\mathrm{s}}=-45\,\frac{\mathrm{m}}{\mathrm{s}}}

y la rapidez

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle |v|= +45\,\frac{\mathrm{m}}{\mathrm{s}}}

Velocidad media

Para la velocidad media necesitamos el desplazamiento, para el cual primero debemos hallar la posición como función del tiempo

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x=x_0+\int_0^t v\,\mathrm{d}t=\frac{3}{2}t^2-\frac{1}{4}t^3}

que en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=10\,\mathrm{s}} es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x(10)= -100\,\mathrm{m}}

lo que nos da la velocidad media

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_m= \frac{x(10)-x(0)}{10\,\mathrm{s}}=-10\,\frac{\mathrm{m}}{\mathrm{s}}}

Distancia total recorrida

La distancia recorrida no coincide con el desplazamiento porque la velocidad cambia de signo.

El cambio de signo se produce cuando la velocidad se anula lo que ocurre en

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3t-\frac{3}{4}t^2=0\qquad\Rightarrow\qquad \left\{\begin{array}{rcl}t & = & 0\,\mathrm{s} \\ && \\ t & = & 4\,\mathrm{s}\end{array}\right.}

El desplazamiento entre t = 0 s y t = 4 s es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta x_1 = x(4\,\mathrm{s})-x(0\,\mathrm{s})=\frac{3}{2}4^2-\frac{1}{4}4^3 = 8\,\mathrm{m}}

y entre t = 4 s y t = 10 s

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta x_2 = x(10\,\mathrm{s})-x(4\,\mathrm{s})=-100-8 = -108\,\mathrm{m}}

Por tanto la distancia total recorrida vale

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta s = |\Delta x_1|+|\Delta x_2| = 116\,\mathrm{m}}

Rapidez media

La rapidez media es la distancia total recorrida dividida por el intervalo de tiempo empleado

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle |v|_m=\frac{\Delta s}{\Delta t}=\frac{116\,\mathrm{m}}{10\,\mathrm{s}}=1.16\,\frac{\mathrm{m}}{\mathrm{s}}}