Introducción
Los principios de la dinámica o Leyes de Newton son los axiomas por los que se rigen las partículas y sistemas en la dinámica clásica. Fueron enunciados por Newton, basándose en los trabajos de Galileo, en sus Principia Mathematica.
Aunque se refieren a partículas, la aplicación directa de las leyes de Newton es mucho más amplia:
- Se aplican a toda clase de objetos cuyo tamaño es mucho menor que las distancias que recorre. Así, la Tierra, en su movimiento alrededor del Sol, puede ser tratada como una partícula.
- Se aplican directamente a sólidos, cuando no hay rotación de estos. Por ejemplo, una masa que desliza por un plano inclinado. Cuando hay rotación, deben emplearse ecuaciones más complicadas (ecuaciones de Euler) que se deducen de las leyes de Newton.
- Son suficientes para explicar el movimiento del centro de masas de un sistema de partículas, el cual se mueve como si toda la masa del sistema estuviera concentrada en él.
- Constituyen una primera aproximación a sistemas que no son partículas pero en el que los efectos de la rotación o deformación son pequeños.
Aparte, las leyes de Newton constituyen la base sobre la que se apoya el resto de la Dinámica.
Una versión de estos principios, enunciada de forma moderna, es la siguiente, donde encabezamos cada principio con el nombre con el que se lo conoce habitualmente:
Primer principio: Principio de inercia
El primer principio de la dinámica, también conocido como Primera Ley de Newton puede formularse como
- “Toda partícula sobre la que no actúa ninguna fuerza permanece en reposo o en estado de movimiento rectilíneo y uniforme, cuando se observa desde un sistema de referencia inercial.”
Este principio fue enunciado inicialmente por Galileo. Galileo llego a él realizando experimentos con bolas que rodaban por canales en planos inclinados. Observó que si la pendiente era hacia abajo, la bola se aceleraba, mientras que si era hacia arriba se frenaba. La conclusión es que en una superficie horizontal debería permanecer constante (aunque la experiencia era que también se frenaba). Explicó el frenado horizontal como consecuencia del rozamiento.

Lo que nos dice esta ley es que el espacio que nos rodea no está curvado de ninguna forma ya que las trayectorias de las partículas libres de interacciones son rectas y no otras curvas, como circunferencias (como ocurriría en la superficie de una esfera) o hélices (como ocurriría en la superficie de un cilindro).
Esta ley contradice ciertas intuiciones comunes pero incorrectas:
- Aristóteles pensaba que para que un objeto se moviera era necesaria siempre una fuerza. En ausencia de fuerza, un objeto se para. Esto es incorrecto porque no tiene en cuenta el rozamiento como una fuerza más. Si no hubiera rozamiento alguno, un objeto no se pararía. Así, por ejemplo, una nave que viaja por el espacio no necesita activar sus motores la mayor parte del tiempo (independientemente de lo que se vea en las películas).

- En la Edad Media, se consideraba que cuando se lanzaba un objeto (como una piedra), se le comunicaba una fuerza y que cuando viajaba por el aire era porque seguía actuando "la fuerza con que se había lanzado", la cual se iba agotando progresivamente. Esto también es falso. La fuerza de lanzamiento solo actúa en el instante inicial. Posteriormente, sólo el peso y el rozamiento son responsables del movimiento de la partícula.
El primer principio de la dinámica conlleva la clasificación de los sistemas de referencia en inerciales (aquellos desde los cuales una partícula libre de interacciones se observa en reposo o movimiento rectilíneo y uniforme) y no inerciales (aquellos respecto a los que no se cumple este principio de inercia).
Dado un sistema inercial, se puede identificar al resto de sistemas inerciales como aquellos que tienen velocidad constante (es decir, aceleración nula) respecto al primero. Un sistema de referencia no inercial es aquel que está acelerado respecto a uno inercial.
Dos sistemas de referencia inerciales diferentes, y miden distintas posiciones, velocidades y aceleraciones para la misma partícula. No obstante, pueden relacionarse estas medidas.
Si el punto es el origen del sistema y el del sistema , la posición del punto P en cada sistema verifica
Las velocidades cumplen el llamado principio de relatividad de Galileo
siendo la velocidad del sistema de referencia 0 respecto al 1. En este contexto, a esta velocidad se denomina velocidad de arrastre, mientras que y se denominan la velocidad absoluta y la relativa, respectivamente.
Puesto que los dos sistemas son inerciales la velocidad de arrastre es una constante. Esto implica, al derivar respecto al tiempo, que las aceleraciones que miden los dos observadores son iguales
En este contexto se dice que la aceleración es un invariante.
Es fácil ver que en un sistema acelerado no se cumple la ley de inercia. Consideremos una plataforma giratoria respecto al suelo, que es un sistema inercial. Una pelota lanzada por el aire por encima de la plataforma describe en la horizontal un movimiento rectilíneo y uniforme. Sin embargo, para un observador situado sobre la plataforma, la pelota se desvía lateralmente hacia un lado y por tanto no describe un movimiento rectilíneo y uniforme, pese a que no hay fuerzas horizontales actuando sobre ella.
| Desde el suelo | Desde la plataforma |
|---|---|
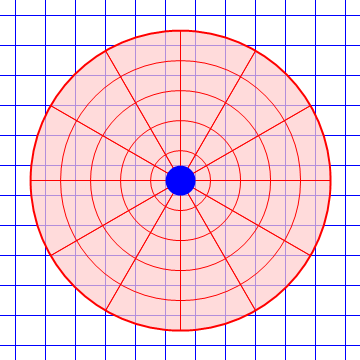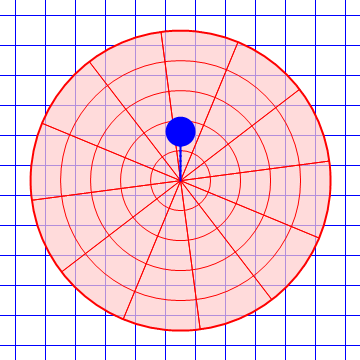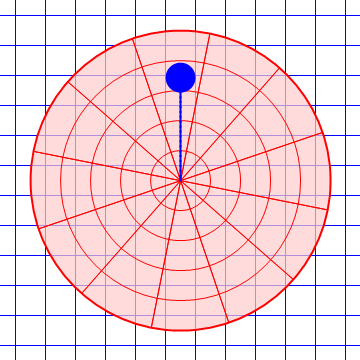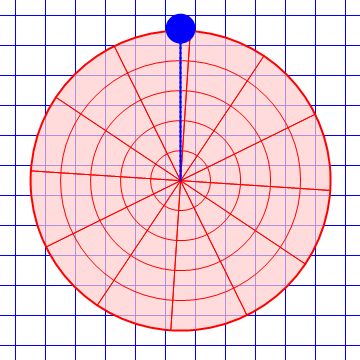
|
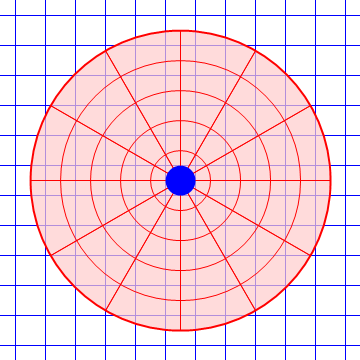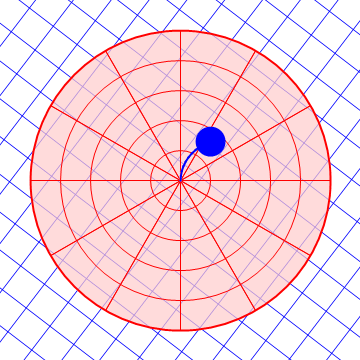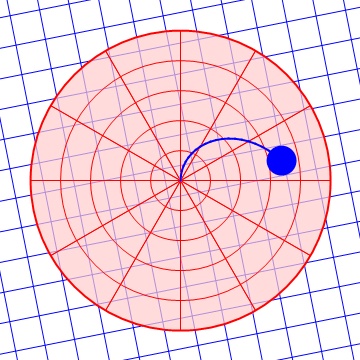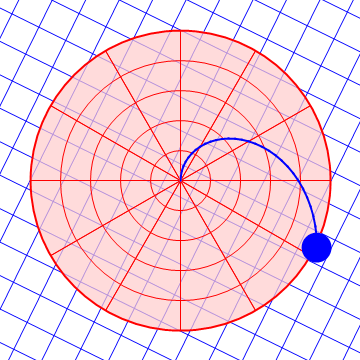
|
¿Es la Tierra un sistema de referencia inercial? Respecto al espacio que la rodea la aceleración de un sistema de referencia ligado a la Tierra se debe a la rotación de esta sobre sí misma y a la de traslación respecto al Sol. Ambas pueden calcularse empleando la expresión para la aceleración en un movimiento circular uniforme . A partir de los periodos de rotación y traslación pueden hallarse las aceleraciones correspondientes y resulta un valor de 0.03 m/s² para la de rotación y una de 0.006 m/s² para la de traslación. La segunda es muy pequeña comparada con la de la gravedad, pero la primera no tanto. Por ello en fenómenos que requieren un tiempo largo o grandes distancias, como los que se estudian en meteorología, el efecto de la rotación terrestre es importante y en ocasiones dominante.
Segundo principio: Segunda Ley de Newton
Cuando sobre un cuerpo se aplica una fuerza, éste deja de realizar un movimiento rectilíneo y uniforme, esto es, su velocidad deja de ser constante. El segundo principio de la dinámica nos dice qué es lo que ocurre cuando a una partícula se le aplica una fuerza
- “Cuando sobre un cuerpo de masa se aplica una fuerza neta adquiere una aceleración proporcional a la fuerza aplicada e inversamente proporcional a la masa del cuerpo”
o, como se escribe habitualmente
Si hay más de una fuerza aplicada simultáneamente, es la resultante de las fuerzas aplicadas sobre la partícula, hallada como suma vectorial de ellas.
Así, por ejemplo, para un avión en vuelo se considera que está sometido a cuatro fuerzas: su peso, la sustentación debida al aire, el empuje o tracción debido a la propulsión y la resistencia debida a la fricción con el aire

Dependiendo del balance entre las diferentes fuerzas se obtiene la aceleración en la dirección deseada. Cuando el avión vuela a velocidad constante, quiere decir que la suma de las fuerzas aplicadas es nula.
Cuando actúan varias fuerzas independientes, sus efectos se suman, según el
- Principio de superposición
- Si sobre un mismo punto material actúan dos fuerzas simultáneamente, la aceleración que adquiere es la suma vectorial de las aceleraciones que le comunicarían cada una de las dos fuerzas por separado.
- También se conoce a éste como principio de independencia de acción de las fuerzas, y se puede generalizar para un número arbitrario de fuerzas.
Masa e inercia
En la segunda ley de Newton
aparece la masa de la partícula como la constante de proporcionalidad entre fuerza y aceleración. Tradicionalmente la masa se considera como una medida de la cantidad de materia, sin embargo, para expresar esa idea ya existe otra magnitud fundamental, cuya unidad es el mol.
En este contexto la masa es una propiedad de la partícula que mide su inercia. Puesto que aparece en un denominador, para una fuerza aplicada dada, cuanto mayor es la masa, menor es la aceleración. Si la aceleración es menor, el cambio de velocidad es también menor. Por tanto, cuanto mayor es la masa, menos cambia la velocidad, es decir, es más difícil modificar el estado de movimiento de la partícula. A esta oposición al cambio del estado se la denomina inercia y a la propiedad que la mide, masa inercial.
Un ejemplo claro del significado de la inercia lo tenemos en la fuerza necesaria para tomar una curva. Supongamos un coche y un camión que deben tomar ambos la misma curva con rapidez constante. En este caso la aceleración es puramente normal, por lo que se cumple la relación
Esta ecuación puede leerse de diferentes formas:
- Si los dos vehículos toman la curva con la misma rapidez, el del camión deberá realizar una fuerza mayor, proporcionalmente a la masa.
- Si los dos vehículos realizan la misma fuerza, el camión deberá circular más despacio, con una rapidez proporcional a la inversa de la raíz cuadrada de la masa.
- Si los dos vehículos entran en la curva con la misma rapidez y realizan la misma fuerza, el radio de curvatura del camión es mayor, proporcionalmente a la masa, lo que quiere decir que “hace un recto” y se sale de la curva
Leyes de fuerza
La segunda ley de Newton requiere el conocimiento de las fuerzas aplicadas, como un dato del problema. Estas fuerzas deben ser obtenidas independientemente para que la ley tenga verdadero significado. Por ello, precisamos de algún modelo físico que nos proporcione la expresión de la fuerza. Entre estos modelos se encuentran:
- La ley de Hooke, para el oscilador armónico
- La ley de Newton de la Gravitación Universal, para el movimiento de una masa en el campo gravitatorio de otra
- En esta ley aparece también la masa, como creadora de campo gravitatorio (la denominada masa gravitatoria). Newton, estableció que la masa inercial y la gravitatoria tenían el mismo valor, aunque no pudo explicar por qué.
- La ley de la Gravitación contiene al caso particular e importante del movimiento de una masa pequeña en las proximidades de la superficie terrestre
- La ley de Lorentz, para el movimiento de una partícula en un campo electromagnético
- Un caso particular de esta ley es la ley de Coulomb, para la fuerza producida por una carga en reposo
Una característica común a todas estas leyes de fuerza es que proporcionan una fuerza dependiente de la posición y de la velocidad instantáneas de la partícula.
Expresión en componentes
Cartesianas
Separando en las componentes cartesianas quedan las tres ecuaciones escalares
Si cada componente de la fuerza depende solo de la coordenada correspondiente, estas ecuaciones se pueden resolver por separado y el movimiento a lo largo de cada eje es independiente de los otros dos. En la mayoría de los casos, no obstante, las componentes de la fuerza dependen de todas las coordenadas y estas ecuaciones están acopladas. No podemos resolver una sin resolver las otras dos al mismo tiempo.
Polares y cilíndricas
En el caso de un movimiento en un plano también pueden usarse las coordenadas polares. Sustituyendo la expresión de la aceleración en estas componentes quedan las ecuaciones
siendo y las componentes radial y acimutal de la fuerza.
En un movimiento tridimensional, puede incluirse una tercera coordenada perpendicular a este plano. Se dice entonces que tenemos coordenadas cilíndricas. La segunda ley de Newton se escribe en ellas
Intrínsecas
Si descomponemos la fuerza en sus componentes paralela y perpendicular a la velocidad instantánea
quedan las ecuaciones para las componentes intrínsecas de la aceleración
Obsérvese que, como consecuencia de la 2ª ley de Newton, la resultante en la dirección binormal debe ser siempre nula
Tercer principio: ley de acción y reacción
Los dos primeros principios de la dinámica nos dicen cómo se comportan las partículas en ausencia de fuerzas o sometidas a una fuerza conocida. El tercer principio de la dinámica establece una propiedad básica de esas fuerzas de interacción entre partículas:
- “Si una partícula A ejerce en un instante dado una fuerza sobre una partícula B, la partícula B ejerce sobre A una fuerza de igual módulo e igual dirección, pero de sentido contrario.”
Matemáticamente
Hay que destacar que estas dos fuerzas no se anulan mutuamente, ya que se ejercen sobre partículas distintas. Sólo en el caso de que se encuentren rígidamente unidas se cancelarán sus efectos.
Además se cumple para casi todas las fuerzas que el par acción-reacción va en la dirección de la recta que une las dos partículas

Ambas fuerzas actúan simultáneamente. Por ello, hay que señalar que el nombre de “acción y reacción”, con el que se conoce habitualmente a esta ley, es engañoso en cuanto a que sugiere a que primero actúa la acción y posteriormente la reacción. No es así y no existe distinción alguna que convierta a una de las fuerzas en acción y a la otra en reacción.
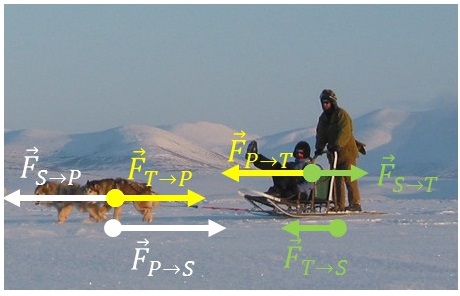
En el caso del trineo arrastrado por perros, el trineo tira del perro exactamente con la misma fuerza, en módulo y dirección, y de sentido opuesto, con la que el perro tira del trineo. ¿Cómo se mueve entonces?
En este sistema, tenemos tres pares acción-reacción:
- El perro y el trineo, cuyas fuerzas se anulan mutuamente, por estar atados rígidamente.
- El perro empuja al suelo hacia atrás, y éste al perro hacia adelante.
- El trineo, que también roza, empuja al suelo hacia adelante, y el suelo empuja al trineo hacia atrás.
Puesto que el rozamiento del trineo sobre la nieve es pequeño, la fuerza del suelo sobre el perro, hacia adelante, supera a la fuerza sobre el trineo hacia atrás, por lo que el sistema puede acelerarse hacia adelante.
Cuando caminamos ejercemos una fuerza hacia atrás sobre el suelo que es respondida por el rozamiento con una hacia adelante del suelo sobre nosotros, que es la que nos permite avanzar.
Del mismo modo, al saltar es la fuerza hacia arriba ejercida por el suelo la que nos eleva. El suelo se comporta como una cama elástica, solo que su deformación es muy pequeña y no la apreciamos.
Sobre la acción y la reacción existen una serie de errores comunes, que se deben evitar:
- Como se ha dicho, la acción y la reacción se aplican sobre cuerpos diferentes. Por tanto, no se anulan mutuamente.
- Un par de fuerzas opuestas aplicadas en el mismo cuerpo no constituyen un par acción-reacción. Así, en el ejemplo del avión, la sustentación y el peso no son acción y reacción.
- En la misma línea, no hay confundir las fuerzas de reacción vincular con un par acción-reacción. Un libro situado sobre una mesa experimenta su peso y la reacción de la mesa, pero estas dos fuerzas no constituyen un par. La reacción al peso es la atracción que el libro ejerce sobre la Tierra, y que se situará en el centro de ésta. La fuerza ejercida por la mesa es la reacción de las fuerzas (electromagnéticas) que el libro ejerce sobre ella, debido a la compresión de sus átomos.
- No hay que mezclar acción y reacción con fuerzas de inercia. La fuerza centrífuga no es la reacción a la centrípeta, entre otras cosas, porque la fuerza centrífuga es una fuerza ficticia.


































