Diferencia entre revisiones de «Cuatro cargas en dos varillas»
(Página creada con «==Enunciado== Se tiene el sistema de 4 cargas de la figura, a la izquierda hay dos cargas iguales +''q'', unidas por una varilla rígida (sin carga). A la derecha hay otra varilla rígida, en cuyos extremos hay cargas opuestas ±''q''. Las cuatro cargas forman un cuadrado de lado ''b''. Para cada varilla, calcule la fuerza resultante y el momento resultante respecto a su centro de masas (centro de cada varilla). centro ==Varilla…») |
Sin resumen de edición |
||
| (No se muestran 3 ediciones intermedias del mismo usuario) | |||
| Línea 7: | Línea 7: | ||
==Varilla izquierda== | ==Varilla izquierda== | ||
===Fuerza resultante=== | ===Fuerza resultante=== | ||
La fuerza sobre cada carga es la suma de las debidas a las dos cargas de la varilla de la derecha. A su vez, la fuerza resultante sobre la varilla izquierda es la suma de las fuerzas sobre cada una de sus cargas. Si llamamos 1 y 2 a las cargas de la varilla izquierda y 3 y 4 a las de la derecha (de arriba abajo en ambos casos), la fuerza resultante es | La fuerza sobre cada carga es la suma de las debidas a las dos cargas de la varilla de la derecha. A su vez, la fuerza resultante sobre la varilla izquierda es la suma de las fuerzas sobre cada una de sus cargas. | ||
[[Archivo:cuadrado-cargas-fuerzas.png|500px|center]] | |||
Si llamamos 1 y 2 a las cargas de la varilla izquierda y 3 y 4 a las de la derecha (de arriba abajo en ambos casos), la fuerza resultante es | |||
<center><math>\vec{F}_I=\vec{F}_{3\to 1}+\vec{F}_{4\to 1}+\vec{F}_{3\to 2}+\vec{F}_{4\to 2}</math></center> | <center><math>\vec{F}_I=\vec{F}_{3\to 1}+\vec{F}_{4\to 1}+\vec{F}_{3\to 2}+\vec{F}_{4\to 2}</math></center> | ||
| Línea 33: | Línea 37: | ||
La suma de estas cuatro cantidades es | La suma de estas cuatro cantidades es | ||
<center><math>\vec{F}_I = F_0\left(-\vec{\imath}+\frac{1}{2\sqrt{2}}(\vec{\imath} -\vec{\jmath})+\frac{1}{2\sqrt{2}}(-\vec{\imath} -\vec{\jmath})+\vec\imath}\right)=-\frac{F_0}{\sqrt{2}}\vec{\jmath}</math></center> | <center><math>\vec{F}_I = F_0\left(-\vec{\imath}+\frac{1}{2\sqrt{2}}(\vec{\imath} -\vec{\jmath})+\frac{1}{2\sqrt{2}}(-\vec{\imath} -\vec{\jmath})+\vec{\imath}\right)=-\frac{F_0}{\sqrt{2}}\vec{\jmath}</math></center> | ||
Vemos que resulta una fuerza neta que ni es de atracción ni de repulsión, sino que va dirigida a lo largo de la varilla. | Vemos que resulta una fuerza neta que ni es de atracción ni de repulsión, sino que va dirigida a lo largo de la varilla. | ||
[[Archivo:suma-cuadrado-cargas-fuerzas.png|350px|center]] | |||
===Momento resultante=== | ===Momento resultante=== | ||
Para el momento resultante tenemos que, respecto al centro de la varilla | |||
<center><math>\vec{M}_{G_I}=\left(\frac{b}{2}\vec{\jmath}\right)\times\left(\vec{F}_{3\to 1}+\vec{F}_{4\to 1}\right)+\left(-\frac{b}{2}\vec{\jmath}\right)\times\left(\vec{F}_{3\to 2}+\vec{F}_{4\to 2}\right)</math></center> | |||
Esto nos da | |||
<center><math>\vec{M}_{G_I}=F_0b\left(1 - \frac{1}{2\sqrt{2}}\right)\vec{k}</math></center> | |||
==Varilla derecha== | ==Varilla derecha== | ||
===Fuerza resultante=== | |||
Para la fuerza resultante sobre la varilla derecha podemos hacer también la suma vectorial de las cuatro fuerzas, pero es más simple aplicar la tercera ley de Newton. | Para la fuerza resultante sobre la varilla derecha podemos hacer también la suma vectorial de las cuatro fuerzas, pero es más simple aplicar la tercera ley de Newton. | ||
<center><math>\vec{F}_D=-\vec{F}_I = \frac{F_0}{\sqrt{2}}\vec{\jmath}</math></center> | <center><math>\vec{F}_D=-\vec{F}_I =+\frac{F_0}{\sqrt{2}}\vec{\jmath}</math></center> | ||
===Momento resultante=== | |||
Respecto al centro de esta varilla | |||
<center><math>\vec{M}_{G_D}=\left(\frac{b}{2}\vec{\jmath}\right)\times\left(\vec{F}_{1\to 3}+\vec{F}_{2\to 3}\right)+\left(-\frac{b}{2}\vec{\jmath}\right)\times\left(\vec{F}_{1\to 4}+\vec{F}_{2\to 4}\right)</math></center> | |||
que da como resultado | |||
<center><math>\vec{M}_{G_D}=F_0b\left(-1 - \frac{1}{2\sqrt{2}}\right)\vec{k}</math></center> | |||
No salen momentos opuestos porque están calculados respecto a puntos diferentes. El momento respecto al centro de la varilla derecha podría haberse calculado sin necesidad de sumar las fuerzas individuales usando las propiedades de los momentos en un sistema de fuerzas | |||
<center><math>\vec{M}_{G_D}=\vec{M}_{G_I}+\vec{F}_D\times\overrightarrow{G_IG_D}</math></center> | |||
El primero de los dos sumandos sí es el opuesto al clau | |||
Revisión actual - 14:30 10 abr 2024
Enunciado
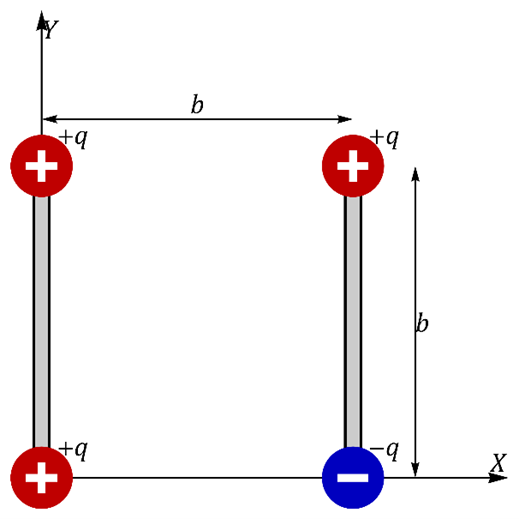
Se tiene el sistema de 4 cargas de la figura, a la izquierda hay dos cargas iguales +q, unidas por una varilla rígida (sin carga). A la derecha hay otra varilla rígida, en cuyos extremos hay cargas opuestas ±q. Las cuatro cargas forman un cuadrado de lado b.
Para cada varilla, calcule la fuerza resultante y el momento resultante respecto a su centro de masas (centro de cada varilla).
Varilla izquierda
Fuerza resultante
La fuerza sobre cada carga es la suma de las debidas a las dos cargas de la varilla de la derecha. A su vez, la fuerza resultante sobre la varilla izquierda es la suma de las fuerzas sobre cada una de sus cargas.
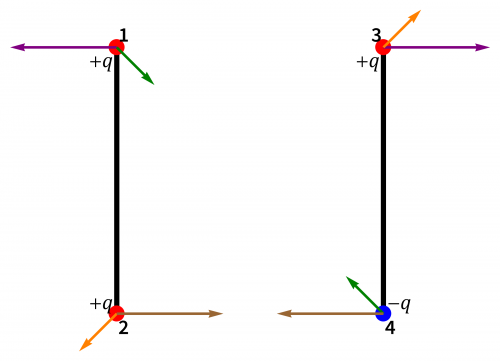
Si llamamos 1 y 2 a las cargas de la varilla izquierda y 3 y 4 a las de la derecha (de arriba abajo en ambos casos), la fuerza resultante es
Para cada una de ellas, se cumple
Tenemos que
donde llamamos , cantidad que aparecerá repetidamente. Para el siguiente par
y de la misma manera
y
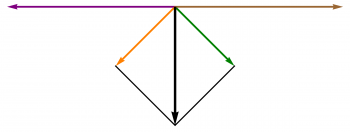
La suma de estas cuatro cantidades es
Vemos que resulta una fuerza neta que ni es de atracción ni de repulsión, sino que va dirigida a lo largo de la varilla.
Momento resultante
Para el momento resultante tenemos que, respecto al centro de la varilla
Esto nos da
Varilla derecha
Fuerza resultante
Para la fuerza resultante sobre la varilla derecha podemos hacer también la suma vectorial de las cuatro fuerzas, pero es más simple aplicar la tercera ley de Newton.
Momento resultante
Respecto al centro de esta varilla
que da como resultado
No salen momentos opuestos porque están calculados respecto a puntos diferentes. El momento respecto al centro de la varilla derecha podría haberse calculado sin necesidad de sumar las fuerzas individuales usando las propiedades de los momentos en un sistema de fuerzas
El primero de los dos sumandos sí es el opuesto al clau













