Diferencia entre las páginas «Metrología (G.I.T.I.)» y «Tabla de fórmulas de trigonometría»

Revisión actual - 13:13 21 sep 2023

Ángulos

Definición

Complementario y suplementario

Complementario

Suplementario

Opuestos por el vértice y alternos

Rotación de ejes

Mismo origen

Diferente origen

Definiciones

Geométrica

Coseno: $\cos(x)={\frac {a}{r}}$
Seno: $\mathrm {sen} (x)={\frac {b}{r}}$

Analítica

El argumento $x$ debe estar expresado en radianes

\cos(x)=1-{\frac {x^{2}}{2}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots

\mathrm {sen} (x)=x-{\frac {x^{3}}{6}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots

Exponenciales complejas

(

\mathrm {j} ={\sqrt {-1}}

)

\cos(x)={\frac {\mathrm {e} ^{\mathrm {j} x}+\mathrm {e} ^{-\mathrm {j} x}}{2}}

\mathrm {sen} (x)={\frac {\mathrm {e} ^{\mathrm {j} x}-\mathrm {e} ^{-\mathrm {j} x}}{2\mathrm {j} }}

Funciones adicionales

Tangente: $\mathrm {tg} (x)={\frac {\mathrm {sen} (x)}{\cos(x)}}={\frac {b}{a}}$

Cotangente: $\mathrm {cotg} (x)={\frac {\cos(x)}{\mathrm {sen} (x)}}={\frac {1}{\mathrm {tg} (x)}}={\frac {a}{b}}$

Secante: $\mathrm {sec} (x)={\frac {1}{\cos(x)}}={\frac {r}{a}}$

Cosecante: $\mathrm {cosec} (x)={\frac {1}{\mathrm {sen} (x)}}={\frac {r}{b}}$

En la circunferencia unidad

Gráficas desde −π a π

Seno y coseno

Tangente y cotangente

Secante y cosecante

Relaciones entre funciones

Identidades básicas

\cos ^{2}(x)+\mathrm {sen} ^{2}(x)=1\,

1+\mathrm {tg} ^{2}(x)=\mathrm {sec} ^{2}(x)={\frac {1}{\cos ^{2}(x)}}\,

\mathrm {cotg} ^{2}(x)+1=\mathrm {cosec} ^{2}(x)={\frac {1}{\mathrm {sen} ^{2}(x)}}\,

En función de la tangente

u=\mathrm {tg} (x)\,

\mathrm {sen} (x)={\frac {u}{\sqrt {1+u^{2}}}}

\cos(x)={\frac {1}{\sqrt {1+u^{2}}}}

En función de la tangente del ángulo mitad

u=\mathrm {tg} \left({\frac {x}{2}}\right)\,

\mathrm {sen} (x)={\frac {2u}{1+u^{2}}}

\cos(x)={\frac {1-u^{2}}{1+u^{2}}}

\mathrm {tg} (x)={\frac {2u}{1-u^{2}}}

Tabla de valores particulares

°	rad	sen	cos	tg
$0\,$	$0\,$	${\sqrt {0}}/2=0$	$1\,$	$0\,$
$30\,$	$\pi /6\,$	${\sqrt {1}}/2=1/2\,$	${\sqrt {3}}/2$	$1/{\sqrt {3}}$
$45\,$	$\pi /4\,$	${\sqrt {2}}/2$	${\sqrt {2}}/2$	$1\,$
$60\,$	$\pi /3\,$	${\sqrt {3}}/2$	$1/2\,$	${\sqrt {3}}$
$90\,$	$\pi /2\,$	${\sqrt {4}}/2=1$	$0\,$	$\infty$

Relaciones entre cuadrantes

Ángulo complementario

\mathrm {sen} \left({\frac {\pi }{2}}-x\right)=\cos(x)\qquad \cos \left({\frac {\pi }{2}}-x\right)=\mathrm {sen} (x)

Ángulo suplementario: $\mathrm {sen} \left(\pi -x\right)=\mathrm {sen} (x)\qquad \cos \left(\pi -x\right)=-\cos(x)$

Giro de un cuadrante: $\mathrm {sen} \left({\frac {\pi }{2}}+x\right)=\cos(x)\qquad \cos \left({\frac {\pi }{2}}+x\right)=-\mathrm {sen} (x)$

Giro de dos cuadrantes: $\mathrm {sen} \left(\pi +x\right)=-\mathrm {sen} (x)\qquad \cos \left(\pi +x\right)=-\cos(x)$

Cambio de signo: $\mathrm {sen} \left(-x\right)=-\mathrm {sen} (x)\qquad \cos \left(-x\right)=\cos(x)$

Suma y diferencia de ángulos

Seno

\mathrm {sen} (x+y)=\mathrm {sen} (x)\cos(y)+\cos(x)\mathrm {sen} (y)\,

\mathrm {sen} (x-y)=\mathrm {sen} (x)\cos(y)-\cos(x)\mathrm {sen} (y)\,

Coseno

\cos(x+y)=\cos(x)\cos(y)-\mathrm {sen} (x)\mathrm {sen} (y)\,

\cos(x-y)=\cos(x)\cos(y)+\mathrm {sen} (x)\mathrm {sen} (y)\,

Tangente

\mathrm {tg} (x+y)={\frac {\mathrm {tg} (x)+\mathrm {tg} (y)}{1-\mathrm {tg} (x)\mathrm {tg} (y)}}

\mathrm {tg} (x-y)={\frac {\mathrm {tg} (x)-\mathrm {tg} (y)}{1+\mathrm {tg} (x)\mathrm {tg} (y)}}

Ángulo doble y ángulo mitad

Ángulo doble

Seno

\mathrm {sen} (2x)=2\,\mathrm {sen} (x)\cos(x)\,

Coseno

\cos(2x)=\cos ^{2}(x)-\mathrm {sen} ^{2}(x)\,

Tangente

\mathrm {tg} (2x)={\frac {2\,\mathrm {tg} (x)}{1-\mathrm {tg} ^{2}(x)}}

Ángulo mitad

Seno

\mathrm {sen} \left({\frac {x}{2}}\right)={\sqrt {\frac {1-\cos(x)}{2}}}

Coseno

\cos \left({\frac {x}{2}}\right)={\sqrt {\frac {1+\cos(x)}{2}}}

Tangente

\mathrm {tg} \left({\frac {x}{2}}\right)={\sqrt {\frac {1-\cos(x)}{1+\cos(x)}}}={\frac {\mathrm {sen} (x)}{1+\cos(x)}}

Sumas en productos

\mathrm {sen} (x)+\mathrm {sen} (y)=2\,\mathrm {sen} \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)

\mathrm {sen} (x)-\mathrm {sen} (y)=2\,\mathrm {sen} \left({\frac {x-y}{2}}\right)\cos \left({\frac {x+y}{2}}\right)

\cos(x)+\cos(y)=2\cos \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)

\cos(x)-\cos(y)=-2\,\mathrm {sen} \left({\frac {x+y}{2}}\right)\mathrm {sen} \left({\frac {x-y}{2}}\right)

Derivadas y primitivas

El argumento debe estar obligatoriamente en radianes

Derivadas

{\frac {\mathrm {d} \ }{\mathrm {d} x}}(\mathrm {sen} (x))=\cos(x)

{\frac {\mathrm {d} \ }{\mathrm {d} x}}(\cos(x))=-\,\mathrm {sen} (x)

{\frac {\mathrm {d} \ }{\mathrm {d} x}}(\mathrm {tg} (x))={\frac {1}{\cos ^{2}(x)}}=1+\mathrm {tg} ^{2}(x)

Primitivas

\int \mathrm {sen} (x)\mathrm {d} x=-\cos(x)+C

\int \cos(x)\mathrm {d} x=\mathrm {sen} (x)+C

\int \mathrm {tg} (x)\mathrm {d} x=-\ln(\cos(x))+C

Fórmula de Euler

Fórmula general

\mathrm {e} ^{\mathrm {j} x}=\cos(x)+\mathrm {j} \,\mathrm {sen} (x)\qquad (\mathrm {j} ={\sqrt {-1}})

Casos particulares

\mathrm {e} ^{\mathrm {j} \pi /2}=\mathrm {j} \,

\mathrm {e} ^{\mathrm {j} \pi }=-1\,

\mathrm {e} ^{2\pi \mathrm {j} }=1\,

Teoremas del seno y del coseno

Teorema del seno

{\frac {a}{\mathrm {sen} (\alpha )}}={\frac {b}{\mathrm {sen} (\beta )}}={\frac {c}{\mathrm {sen} (\gamma )}}=2R

( $R$ : radio de la circunferencia circunscrita)

Teorema del coseno

Misma notación que en el teorema del seno

a^{2}=b^{2}+c^{2}-2bc\cos(\alpha )\,

y las correspondientes a los otros dos ángulos.

Resolución de triángulos

Misma notación que en el teorema del seno y del coseno.

Se trata de dados tres datos (lados o ángulos) hallar los tres restantes.

Dados los tres lados

Por el teorema del coseno se determinan los tres ángulos. Para $\alpha$

\alpha =\arccos \left({\frac {b^{2}+c^{2}-a^{2}}{2bc}}\right)

y análogamente para los otros dos.

Dados dos lados y el ángulo que abarcan

Si conocemos $a$ , $b$ y el ángulo $\gamma$ por el teorema del coseno hallamos $c$

c={\sqrt {a^{2}+b^{2}-2ab\cos(\gamma )}}

una vez conocidos los tres lados podemos aplicar el caso anterior o bien emplear el teorema del seno

\alpha =\mathrm {arcsen} \left({\frac {a}{c}}\mathrm {sen} (\gamma )\right)

Dados dos lados y otro ángulo

Si conocemos $a$ , $b$ y el ángulo $\beta$ por el teorema del seno hallamos $\alpha$

\alpha =\mathrm {arcsen} \left({\frac {a}{b}}\mathrm {sen} (\beta )\right)

y aplicando que los ángulos suman $\pi$

\gamma =\pi -\alpha -\beta \,

y a partir de ahí se sigue como en los casos anteriores.

Dado un lado y dos ángulos

Si concemos el lado $a$ y los ángulos $\beta$ y $\gamma$ , hallamos en primer lugar $\alpha$

\alpha =\pi -\beta -\gamma \,

y luego aplicamos el teorema del seno

b=a{\frac {\mathrm {sen} (\beta )}{\mathrm {sen} (\alpha )}}\qquad \qquad c=a{\frac {\mathrm {sen} (\gamma )}{\mathrm {sen} (\alpha )}}

Dados los tres ángulos

En ese caso no se pueden dar los tres lados, ya que todos los triángulos semejantes tienen los mismos ángulos independientemente de su tamaño. No obstante, puede darse a proporción entre sus lados mediante el teorema del seno.

@@ Línea 1: / Línea 1: @@
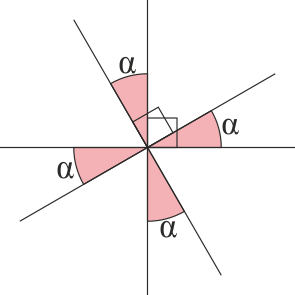
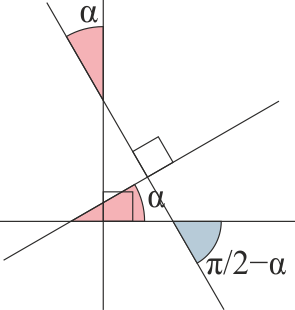
-==Introducción. Objeto de la Física==
+==Ángulos==
-La Física suele entenderse como la ciencia que describe matemáticamente el comportamiento de los sistemas (y del Universo en general) atendiendo a sus propiedades físicas (y no químicas), esto es, masa, posición, velocidad, carga eléctrica, etc.
+===Definición===
+[[Archivo:definicion-angulo.png]]
-Esta definición que, como todas, es parcial e imprecisa, omite un aspecto esencial, el cómo se hace esa descripción matemática del Universo. La Física realmente no describe el Universo o los sistemas, sino que construye un ''modelo matemático'' de ellos.
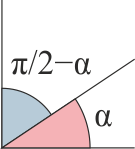
+===Complementario y suplementario===
+;Complementario:
+[[Archivo:complementario.png]]
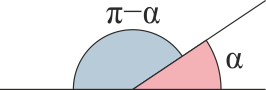
+;Suplementario:
+[[Archivo:suplementario.png]]
-La construcción de estos modelos matemáticos sigue el denominado ''Método Científico'': a partir de una serie de evidencias experimentales, se formulan una serie de postulados, a partir de los cuales se elabora matemáticamente una teoría. Esta teoría debe tener carácter predictivo (si no, no pasaría de pura especulación). Esas predicciones deben poder ser verificables empíricamente, mediante una serie de experimentos más o menos controlados.
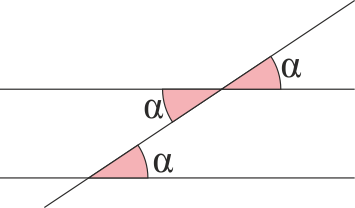
+===Opuestos por el vértice y alternos===
-A partir de los resultados experimentales se establecen los límites de validez de la teoría (el rango dentro del cual es aplicable), se refinan los postulados o, si es preciso, se abandona la teoría y se sustituye por una nueva.
+[[Archivo:opuestos-vertice.png]]
-El que una teoría física sea un modelo matemático basado en una serie de hipótesis razonables provoca que en la elaboración de una teoría aparezcan entes aparentemente inexistentes, como partículas perfectamente puntuales o sólidos absolutamente rígidos. Por ejemplo, una barra de hierro puede describirse como un sólido perfectamente rígido dentro de los límites de validez de la teoría (por ejemplo, al diseñar un mecanismo) aunque dicho modelo deje de ser válido fuera de dichos límites (por ejemplo, si queremos estudiar la deformación de la barra por la fatiga mecánica).
+===Rotación de ejes===
+;Mismo origen:
+[[Archivo:ejes-girados-01.png]]
+;Diferente origen:
+[[Archivo:ejes-girados-02.png]]
-Tanto a la hora de establecer los postulados a partir de los cuales se elabora la teoría, como a la hora de verificar sus predicciones, es esencial la realización de ''medidas''. Una teoría física que no se corresponde con datos experimentales no pasa de la categoría de elucubración.
+==Definiciones==
+===Geométrica===
-==Medidas==
+:[[Archivo:triangulo-rectangulo.png]]
-===Medidas directas e indirectas===
-En su versión más simple, una ''medida'' es la comparación de un resultado experimental con un patrón (''unidad de medida''). Esto es, cuando se dice que una distancia mide 3&thinsp;m lo que se está diciendo es que la longitud medida es 3 veces la de la medida patrón, tomada como 1&thinsp;m.
-A partir de una serie de medidas experimentales directas pueden obtenerse cantidades indirectas o derivadas. Por ejemplo, para medir el área del suelo de una habitación rectangular nos basta con medir las longitudes de dos lados y aplicar la fórmula <math>S = b h</math>. La existencia de estas relaciones permite definir las magnitudes en fundamentales y derivadas.
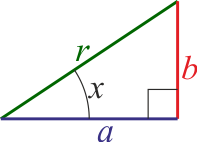
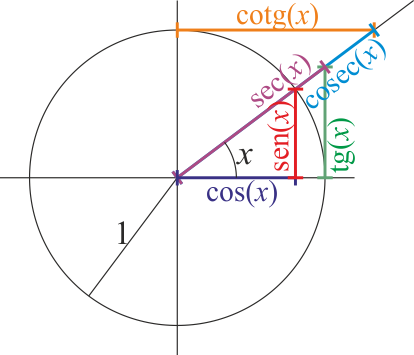
+;Coseno:
+:<math>\cos(x)=\frac{a}{r}</math>
+;Seno:
+:<math>\mathrm{sen}(x) = \frac{b}{r}</math>
-===Dimensiones de una magnitud===
+===Analítica===
-Independientemente de la unidad que se emplee para expresar una magnitud física, esta se caracteriza por sus dimensiones, que no se refiere a su tamaño, sino a que toda magnitud puede expresarse como un producto de potencias de una serie de magnitudes fundamentales. Así, por ejemplo, la velocidad equivale al cociente de una distancia dividida por un intervalo de tiempo y por tanto se verifica la ecuación dimensional
+El argumento <math>x</math> debe estar expresado en radianes
-<center><math>[v] = \frac{[x]}{[t]} = L T^{-1}</math></center>
+:<math>\cos(x) = 1 -\frac{x^2}{2}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots</math>
-donde con el corchete indicamos las dimensiones de la magnitud. Aquí la distancia y el tiempo son consideradas magnitudes fundamentales y la velocidad una magnitud derivada.
+:<math>\mathrm{sen}(x) = x -\frac{x^3}{6}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots</math>
-Las magnitudes que se eligen como fundamentales e incluso el número de ellas es arbitrario. En el SI existen siete magnitudes fundamentales: longitud, tiempo, masa, intensidad de corriente eléctrica, cantidad de materia, temperatura termodinámica e intensidad luminosa. Todas las demás son derivadas.
+===Exponenciales complejas===
+:(<math>\mathrm{j}=\sqrt{-1}</math>)
-Cada magnitud derivada posee una única ecuación dimensional, caracterizada por los diferentes exponentes de las magnitudes fundamentales. Así, por ejemplo, para la fuerza
+:<math>\cos(x) = \frac{\mathrm{e}^{\mathrm{j}x}+\mathrm{e}^{-\mathrm{j}x}}{2}</math>
-<center><math>[F] = M L T^{-2}\,</math></center>
+:<math>\mathrm{sen}(x) = \frac{\mathrm{e}^{\mathrm{j}x}-\mathrm{e}^{-\mathrm{j}x}}{2\mathrm{j}}</math>
-[[Archivo:newcuyama.jpg|thumb|Ejemplo de ecuación dimensionalmente incorrecta]]
+===Funciones adicionales===
-===Homogeneidad dimensional===
+:[[Archivo:triangulo-rectangulo.png]]
-Un principio importante de la física es el de '''homogeneidad dimensional''': en toda ecuación, los dos miembros deben tener las mismas dimensiones. Lo mismo se aplica a toda suma o diferencia. Es el conocido principio de que &ldquo;no se pueden sumar peras con manzanas&rdquo;. Así, por ejemplo, la ecuación
-<center><math>v = \sqrt{2ax}</math></center>
+;Tangente:<math>\mathrm{tg}(x) = \frac{\mathrm{sen}(x)}{\cos(x)} = \frac{b}{a}</math>
-con <math>x</math> la posición, <math>v</math> la velocidad y <math>a</math> la aceleración, cumple
+;Cotangente:<math>\mathrm{cotg}(x) = \frac{\cos(x)}{\mathrm{sen}(x)} = \frac{1}{\mathrm{tg}(x)}=\frac{a}{b}</math>
-<center><math>\frac{L}{T} = \left(1\cdot\frac{L}{T^2}\cdot L\right)^{1/2} = \frac{L}{T}</math></center>
+;Secante:<math>\mathrm{sec}(x) = \frac{1}{\cos(x)}=\frac{r}{a}</math>
-y por tanto es dimensionalmente correcta.
+;Cosecante:<math>\mathrm{cosec}(x) = \frac{1}{\mathrm{sen}(x)}=\frac{r}{b}</math>
-La homogeneidad dimensional permite localizar de forma rápida errores en los resultados de un problema. Así, si en la ecuación anterior hubiéramos omitido el signo de raíz cuadrada el resultado sería dimensionalmente incorrecto y por tanto necesariamente erróneo.
+===En la circunferencia unidad===
-Hay que destacar que la homogeneidad es independiente de las unidades que se empleen para medir las cantidades. Por lo que sabemos, <math>x</math> podría estar medido en leguas, y <math>v</math> en micras/semana. Las dimensiones de una magnitud son algo más básico que las unidades en que se midan.
+[[Archivo:razones-trigonometricas.png]]
-Por ello, una relación entre magnitudes no implica ninguna unidad en concreto (solo las dimensiones) y por tanto es incorrecto escribir una ley como
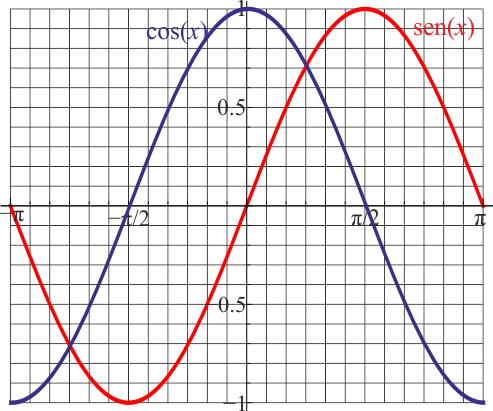
+==Gráficas desde &minus;&pi; a &pi;==
-<center><math>E = \frac{1}{2}mv^2\,(\mathrm{julios})</math>{{qquad}}{{qquad}}(expresión incorrecta)</center>
+;Seno y coseno:
-ya que la energía podría estar expresada en ergios, calorías, kilovatios&middot;hora o muchas otras, dependiendo de en qué midamos la masa o la velocidad. Por ello, la regla es que si una fórmula es puramente algebraica, ''no'' hay que incluir las unidades. Por contra, si se sustituyen uno o todos los valores numéricos, es ''obligatorio'' incluir las unidades.
+:[[Archivo:graf-seno-coseno.png]]
-==Unidades de medida==
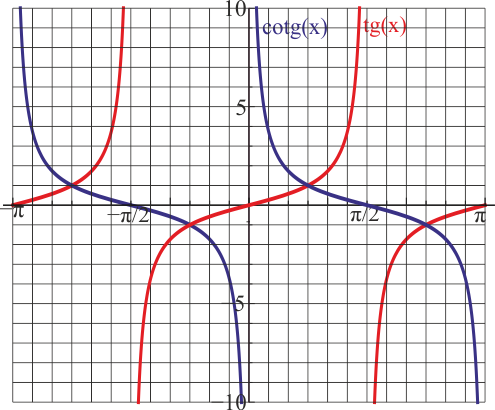
+;Tangente y cotangente
-Las unidades de medida son arbitrarias y, en muchas ocasiones, se definen unidades específicas para un problema concreto. Por ejemplo, cuando se dice que un accidente ocurrió a medio camino entre Sevilla y Madrid, se está tomando como unidad de medida la distancia Sevilla-Madrid y se está diciendo que el accidente ocurrió en <math>x = 0.5u</math>.
-Para poder hacer los resultados fácilmente interpretables y trasladables a otras situaciones, es preferible emplear un sistema de unidades estandarizado. De entre los diferentes sistemas de unidades en uso, el más aceptado y preceptivo legalmente en España, es el Sistema Internacional de Unidades (SI), que ha evolucionado desde el sistema métrico decimal elaborado durante la Revolución Francesa.
+:[[Archivo:graf-tg-cotg.png]]
-===Homogeneidad en las unidades===
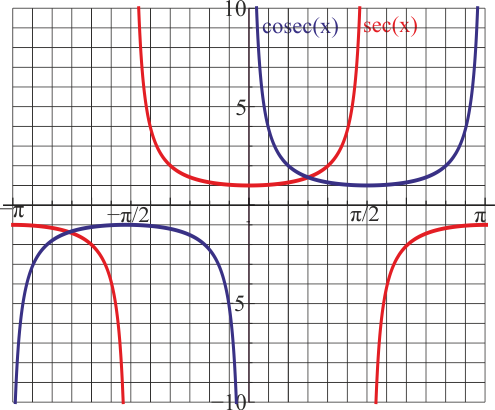
+;Secante y cosecante
-En una fórmula que relaciona valores de diferentes magnitudes, cuando los valores de éstas se sustituyen, incluyendo sus unidades, también debe cumplirse la homogeneidad entre las unidades, esto es, que el primer miembro debe medirse en las mismas unidades que el segundo. Por ejemplo, supongamos que en la ecuación anterior <math>v = \sqrt{2ax}</math>, a = 9.8m/s&sup2; y x = 10&thinsp;km. En ese caso, la velocidad resultante sería
-<center><math>v = \sqrt{2ax}= \sqrt{2\cdot 9.8\frac{\mathrm{m}}{\mathrm{s}^2}\cdot 10\,\mathrm{km}} = 14\,\frac{\sqrt{\mathrm{km}}\sqrt{\mathrm{m}}}{\mathrm{s}}</math></center>
+:[[Archivo:graf-sec-cosec.png]]
-Este resultado, aunque algebraicamente correcto, no posee una forma conveniente por la aparición de potencias fraccionarias de las unidades. Por ello, debe procurarse que el uso de las unidades sea consistente. Expresando la distancia en metros
+==Relaciones entre funciones==
+===Identidades básicas===
-<center><math>v = \sqrt{2ax}= \sqrt{2\cdot 9.8\frac{\mathrm{m}}{\mathrm{s}^2}\cdot 10\,000\mathrm{m}} = 443\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+:<math>\cos^2(x) + \mathrm{sen}^2(x) = 1\,</math>
-Este ejemplo ilustra los peligros de sustituir los valores numéricos de las magnitudes sin incluir sus unidades correspondientes. Una respuesta tal como &ldquo;14&rdquo; sin más datos, a la pregunta de cuál es la velocidad, sería absolutamente errónea.
+:<math>1 + \mathrm{tg}^2(x) = \mathrm{sec}^2(x)=\frac{1}{\cos^2(x)}\,</math>
-===El Sistema Internacional de Unidades===
+:<math>\mathrm{cotg}^2(x) +1= \mathrm{cosec}^2(x)=\frac{1}{\mathrm{sen}^2(x)}\,</math>
-Este sistema de unidades es de obligado cumplimiento en España de acuerdo con el R.D. 2032/2009 (BOE del [http://www.boe.es/boe/dias/2010/01/21/pdfs/BOE-A-2010-927.pdf 21/01/2010], revisado el [http://www.boe.es/boe/dias/2010/02/18/pdfs/BOE-A-2010-2625.pdf 18/02/2010]).
-El SI se basa en siete unidades básicas:
+===En función de la tangente===
-;Metro, m, (longitud): el metro es la longitud del trayecto recorrido en el vacío por la luz durante un tiempo de 1/299&thinsp;792&thinsp;458 de segundo.
+: <math>u = \mathrm{tg}(x)\,</math>
-:De aquí resulta que la velocidad de la luz en el vacío es igual a 299&thinsp;792&thinsp;458 metros por segundo exactamente.
-;Kilogramo, kg (masa): el kilogramo es la unidad de masa; su magnitud se establece mediante la fijación del valor numérico de la constante de Planck, a ser exactamente igual a <math>6,62607015\times10^{-24}</math> cuando es expresada en <math>\mathrm{s^{-1}m^2kg}</math>, que es igual a expresarlo en <math>\mathrm{J\cdot s}</math>. Una definición alternativa equivalente es: el kilogramo es la masa de un cuerpo en reposo cuya energía equivalente es igual a la energía de un conjunto de <math>1.4755214\times10^{40}</math> fotones con la frecuencia de los atomos de cesio utilizados en un reloj atómico (9,192,631,770 Hz)
-;Segundo, s (tiempo): el segundo es la duración de 9&thinsp;192&thinsp;631&thinsp;770 periodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del átomo de cesio 133.
-;Amperio, A (intensidad de corriente eléctrica): el amperio es la intensidad de una corriente constante que, manteniéndose en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y situados a una distancia de 1 metro uno del otro, en el vacío, produciría entre estos conductores una fuerza igual a 2&times;10<sup>&minus;7</sup> newtons por metro de longitud.
-:De aquí resulta que la constante magnética, &mu;<sub>0</sub>, también conocida como permeabilidad del vacío, es exactamente igual a 4&pi;&times;10<sup>&minus;7</sup> H/m.
-;Kelvin, K (temperatura termodinámica): el kelvin es la fracción 1/273.16 de la temperatura termodinámica del punto triple del agua. Esta definición se refiere a un agua de una composición isotópica definida por las siguientes relaciones de cantidad de sustancia: 0.000&thinsp;155&thinsp;76 moles de <sup>2</sup>H por mol de <sup>1</sup>H, 0.000&thinsp;379&thinsp;9 moles de <sup>17</sup>O por mol de <sup>16</sup>O y 0.002&thinsp;005&thinsp;2 moles de <sup>18</sup>O por mol de <sup>16</sup>O.
-:De aquí resulta que la temperatura termodinámica del punto triple del agua es igual a 273.16&thinsp;K.
-;Mol, mol (cantidad de sustancia): el mol es la cantidad de sustancia de un sistema que contiene tantas entidades elementales como átomos hay en 0.012 kilogramos de carbono 12. Esta definición se refiere a átomos de carbono 12 no ligados, en reposo y en su estado fundamental. Cuando se emplee el mol, deben especificarse las entidades elementales, que pueden ser átomos, moléculas, iones, electrones u otras partículas o grupos especificados de tales partículas.
-;Candela, cd (intensidad luminosa): la candela es la intensidad luminosa, en una dirección dada, de una fuente que emite una radiación monocromática de frecuencia 540&times;10<sup>12</sup> hercios y cuya intensidad energética en dicha dirección es de 1/683 vatios por estereorradián.
-A partir de estas unidades básicas se construyen una infinitud de unidades derivadas, mediante productos de potencias de las unidades básicas. Muchas de estas unidades poseen nombre propio, así por ejemplo, 1 hercio (Hz) es igual a 1 s<sup>&minus;1</sup>, 1 newton (N) es igual a 1kg&middot;m/s&sup2; y 1 julio (J) equivale a 1kg&middot;m&sup2;/s&sup2;.
+:<math>\mathrm{sen}(x) = \frac{u}{\sqrt{1+u^2}}</math>
-Mención especial merecen dos unidades adimensionales: el radián (para ángulos planos) y el estereorradián (para ángulos sólidos).
+:<math>\cos(x) = \frac{1}{\sqrt{1+u^2}}</math>
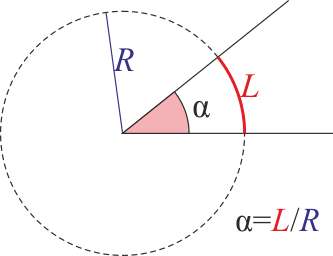
-Un ángulo medido en radianes se define como el cociente entre la longitud de un arco de circunferencia y el radio de dicha circunferencia
+===En función de la tangente del ángulo mitad===
-<center><math>\alpha = \frac{L}{R}</math></center>
+:<math>u = \mathrm{tg}\left(\frac{x}{2}\right)\,</math>
-y por tanto
+:<math>\mathrm{sen}(x) = \frac{2u}{1+u^2}</math>
-<center><math>1\,\mathrm{rad} = \frac{1\,\mathrm{m}}{1\,\mathrm{m}} = 1</math></center>
+:<math>\cos(x) = \frac{1-u^2}{1+u^2}</math>
-Un estereorradián se define como el cociente entre el área de una porción de superficie esférica y el cuadrado del radio de dicha esfera
+:<math>\mathrm{tg}(x) = \frac{2u}{1-u^2}</math>
-<center><math>\Omega = \frac{S}{R^2}</math></center>
+==Tabla de valores particulares==
-y por ello
-<center><math>1\,\mathrm{sr} = \frac{1\,\mathrm{m}^2}{1\,\mathrm{m}^2} = 1</math></center>
-esto es, tanto el radián como el estereorradián son formas diferentes de llamar a la unidad, aportando información sobre la magnitud que miden. Así en la relación entre la frecuencia angular &omega; y la frecuencia natural f
-<center><math>\omega = 2\pi f\,</math></center>
-la primera magnitud de mide en rad/s, mientras que la segunda se mide en Hz = 1/s. Esta ecuación es dimensionalmente correcta, por ser adimensional el radián. Esto quiere decir, en la práctica que el radián y el estereorradián son las únicas unidades que pueden aparecer y desaparecer de las ecuaciones a voluntad.
-===Múltiplos y submúltiplos===
-Las unidades del SI pueden resultar demasiado grandes o demasiado pequeñas para un problema concreto, por lo que se suelen acompañar de prefijos que indican múltiplos
 {| class="bordeado"
-! Prefijo
-! Símbolo
-! 10<sup>n</sup>
-! [[Archivo:spacer.png|300px]]
-|-
-| yotta
-|   Y
-| 10<sup>24</sup>
-| 1&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000
-|-
-| zetta
-|   Z
-| 10<sup>21</sup>
-| 1&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000
 |-
-| exa
+! &deg;
-|   E
+! rad
-| 10<sup>18</sup>
+! sen
-| 1&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000
+! cos
+! tg
 |-
-| peta
+| <math>0\,</math>
-|   P
+| <math>0\,</math>
-| 10<sup>15</sup>
+| <math>\sqrt{0}/2 = 0</math>
-| 1&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000
+| <math>1\,</math>
+| <math>0\,</math>
 |-
-| tera
+| <math>30\,</math>
-|   T
+| <math>\pi/6\,</math>
-| 10<sup>12</sup>
+| <math>\sqrt{1}/2 = 1/2\,</math>
-| 1&thinsp;000&thinsp;000&thinsp;000&thinsp;000
+| <math>\sqrt{3}/2</math>
+| <math>1/\sqrt{3}</math>
 |-
-| giga
+| <math>45\,</math>
-|   G
+| <math>\pi/4\,</math>
-| 10<sup>9</sup>
+| <math>\sqrt{2}/2</math>
-| 1&thinsp;000&thinsp;000&thinsp;000
+| <math>\sqrt{2}/2</math>
+| <math>1\,</math>
 |-
-| mega
+| <math>60\,</math>
-|   M
+| <math>\pi/3\,</math>
-| 10<sup>6</sup>
+| <math>\sqrt{3}/2</math>
-| 1&thinsp;000&thinsp;000
+| <math>1/2\,</math>
+| <math>\sqrt{3}</math>
 |-
-| kilo
+| <math>90\,</math>
-|   k
+| <math>\pi/2\,</math>
-| 10<sup>3</sup>
+| <math>\sqrt{4}/2=1</math>
-| 1&thinsp;000
+| <math>0\,</math>
-|-
+| <math>\infty</math>
-| hecto
-|   h
-| 10<sup>2</sup>
-| 100
-|-
-| deca
-|   da
-| 10<sup>1</sup>
-| 10
 |}
-o submúltiplos
+==Relaciones entre cuadrantes==
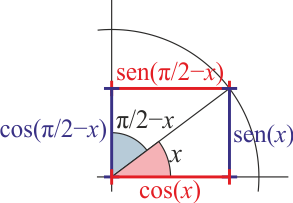
+;Ángulo complementario
+:<math>\mathrm{sen}\left(\frac{\pi}{2}-x\right)=\cos(x)\qquad \cos\left(\frac{\pi}{2}-x\right)=\mathrm{sen}(x)</math>
+:[[Archivo:razones-complementario.png]]
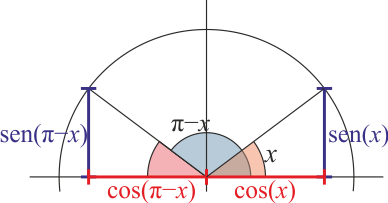
+;Ángulo suplementario
+:<math>\mathrm{sen}\left(\pi-x\right)=\mathrm{sen}(x)\qquad \cos\left(\pi-x\right)=-\cos(x)</math>
+:[[Archivo:razones-suplementario.png]]
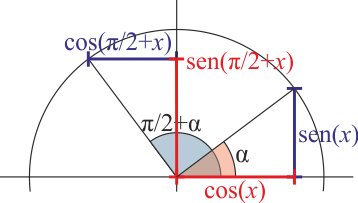
+;Giro de un cuadrante
+:<math>\mathrm{sen}\left(\frac{\pi}{2}+x\right)=\cos(x)\qquad \cos\left(\frac{\pi}{2}+x\right)=-\mathrm{sen}(x)</math>
+:[[Archivo:razones-2o-cuadrante.png]]
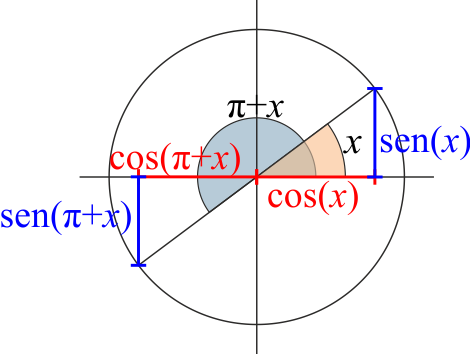
+;Giro de dos cuadrantes
+:<math>\mathrm{sen}\left(\pi+x\right)=-\mathrm{sen}(x)\qquad \cos\left(\pi+x\right)=-\cos(x)</math>
+:[[Archivo:razones-3o-cuadrante.png]]
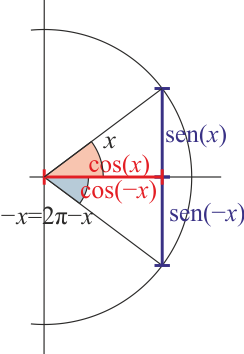
+;Cambio de signo
+:<math>\mathrm{sen}\left(-x\right)=-\mathrm{sen}(x)\qquad \cos\left(-x\right)=\cos(x)</math>
+:[[Archivo:razones-4o-cuadrante.png]]
+==Suma y diferencia de ángulos==
+;Seno:
+:<math>\mathrm{sen}(x+y)=\mathrm{sen}(x)\cos(y)+\cos(x)\mathrm{sen}(y)\,</math>
+:<math>\mathrm{sen}(x-y)=\mathrm{sen}(x)\cos(y)-\cos(x)\mathrm{sen}(y)\,</math>
-{| class="bordeado"
+;Coseno:
-! Prefijo
-! Símbolo
+:<math>\cos(x+y)=\cos(x)\cos(y)-\mathrm{sen}(x)\mathrm{sen}(y)\,</math>
-! 10<sup>n</sup>
-! [[Archivo:spacer.png|300px]]
+:<math>\cos(x-y)=\cos(x)\cos(y)+\mathrm{sen}(x)\mathrm{sen}(y)\,</math>
-|-
-| deci
+;Tangente:
-|   d
-| 10<sup>−1</sup>
+:<math>\mathrm{tg}(x+y)=\frac{\mathrm{tg}(x)+\mathrm{tg}(y)}{1-\mathrm{tg}(x)\mathrm{tg}(y)}</math>
-| 0.1
-|-
+:<math>\mathrm{tg}(x-y)=\frac{\mathrm{tg}(x)-\mathrm{tg}(y)}{1+\mathrm{tg}(x)\mathrm{tg}(y)}</math>
-| centi
-|   c
+==Ángulo doble y ángulo mitad==
-| 10<sup>−2</sup>
+===Ángulo doble===
-| 0.01
+;Seno:
-|-
-| mili
+:<math>\mathrm{sen}(2x)=2\,\mathrm{sen}(x)\cos(x)\,</math>
-|   m
-| 10<sup>−3</sup>
+;Coseno:
-| 0.001
-|-
+:<math>\cos(2x)=\cos^2(x)-\mathrm{sen}^2(x)\,</math>
-| micro
-|   μ
+;Tangente:
-| 10<sup>−6</sup>
-| 0.000&thinsp;001
+:<math>\mathrm{tg}(2x)=\frac{2\,\mathrm{tg}(x)}{1-\mathrm{tg}^2(x)}</math>
-|-
-| nano
+===Ángulo mitad===
-|   n
+;Seno:
-| 10<sup>−9</sup>
-| 0.000&thinsp;000&thinsp;001
+:<math>\mathrm{sen}\left(\frac{x}{2}\right)=\sqrt{\frac{1-\cos(x)}{2}}</math>
-|-
-| pico
+;Coseno:
-|   p
-| 10<sup>−12</sup>
+:<math>\cos\left(\frac{x}{2}\right)=\sqrt{\frac{1+\cos(x)}{2}}</math>
-| 0.000&thinsp;000&thinsp;000&thinsp;001
-|-
+;Tangente:
-| femto
-|   f
+:<math>\mathrm{tg}\left(\frac{x}{2}\right)=\sqrt{\frac{1-\cos(x)}{1+\cos(x)}}=\frac{\mathrm{sen}(x)}{1+\cos(x)}</math>
-| 10<sup>−15</sup>
-| 0.000&thinsp;000&thinsp;000&thinsp;000&thinsp;001
+==Sumas en productos==
-|-
-| atto
+:<math>\mathrm{sen}(x)+\mathrm{sen}(y) = 2\,\mathrm{sen}\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right)</math>
-|   a
-| 10<sup>−18</sup>
+:<math>\mathrm{sen}(x)-\mathrm{sen}(y) = 2\,\mathrm{sen}\left(\frac{x-y}{2}\right)\cos\left(\frac{x+y}{2}\right)</math>
-| 0.000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;001
-|-
+:<math>\cos(x)+\cos(y) = 2\cos\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right)</math>
-| zepto
-|   z
+:<math>\cos(x)-\cos(y) = -2\,\mathrm{sen}\left(\frac{x+y}{2}\right)\mathrm{sen}\left(\frac{x-y}{2}\right)</math>
-| 10<sup>−21</sup>
-| 0.000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;001
+==Derivadas y primitivas==
-|-
+El argumento debe estar obligatoriamente en radianes
-| yocto
+===Derivadas===
-|   y
-| 10<sup>−24</sup>
+:<math>\frac{\mathrm{d}\ }{\mathrm{d}x}(\mathrm{sen}(x)) = \cos(x)</math>
-| 0.000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;000&thinsp;001
-|-
+:<math>\frac{\mathrm{d}\ }{\mathrm{d}x}(\cos(x)) = -\,\mathrm{sen}(x)</math>
-|}
+:<math>\frac{\mathrm{d}\ }{\mathrm{d}x}(\mathrm{tg}(x)) = \frac{1}{\cos^2(x)}=1+\mathrm{tg}^2(x)</math>
+===Primitivas===
+:<math>\int \mathrm{sen}(x)\mathrm{d}x = -\cos(x)+C</math>
+:<math>\int \cos(x)\mathrm{d}x = \mathrm{sen}(x)+C</math>
+:<math>\int \mathrm{tg}(x)\mathrm{d}x = -\ln(\cos(x))+C</math>
+==Fórmula de Euler==
+;Fórmula general
+:<math>\mathrm{e}^{\mathrm{j}x}=\cos(x)+\mathrm{j}\,\mathrm{sen}(x)\qquad (\mathrm{j}=\sqrt{-1})</math>
+;Casos particulares:
+:<math>\mathrm{e}^{\mathrm{j}\pi/2} = \mathrm{j}\,</math>
+:<math>\mathrm{e}^{\mathrm{j}\pi} = -1\,</math>
+:<math>\mathrm{e}^{2\pi\mathrm{j}} = 1\,</math>
-==Conversión de unidades==
+==Teoremas del seno y del coseno==
-Es frecuente la necesidad de transformar una magnitud expresada en ciertas unidades a un sistema de unidades diferente. La forma más sistemática de realizar esta operación es con la ayuda de factores de conversión, que son fracciones cuyo numerador y denominador corresponden al mismo valor de una magnitud, expresada en unidades diferentes. Para transformar una expresión de un sistema a otro se multiplica por los factores de conversión necesarios hasta que el resultado final queda en las unidades deseadas, una vez que se cancelen las unidades que aparecen en las diferentes fracciones.
+===Teorema del seno===
-Así, para pasar de km/h a m/s el procedimiento sería
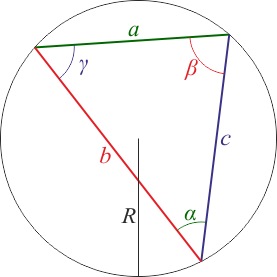
+[[Archivo:teorema-seno.png]]
-<center><math>1\,\frac{\mathrm{km}}{\mathrm{h}} = 1\,\frac{\mathrm{km}}{\mathrm{h}}\times\frac{1000\,\mathrm{m}}{1\,\mathrm{km}}\times\frac{1\,\mathrm{h}}{60\,\mathrm{min}}\times \frac{1\,\mathrm{min}}{60\,\mathrm{s}} = \frac{5}{18}\,\frac{\mathrm{m}}{\mathrm{s}} = 0.2777...\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+:<math>\frac{a}{\mathrm{sen}(\alpha)}=\frac{b}{\mathrm{sen}(\beta)}=\frac{c}{\mathrm{sen}(\gamma)}=2R</math>
-Un procedimiento sistemático para abordar un problema en el que los diferentes datos se den en unidades de sistemas diferentes, consiste en primer lugar en transformar todas las cantidades al SI, operar exclusivamente en este sistema (aunque ello implique el uso de numerosas potencias de 10) y finalmente transformar el resultado final a aquellas unidades que resulten más convenientes.
+(<math>R</math>: radio de la circunferencia circunscrita)
-==Incertidumbre de una medida==
+===Teorema del coseno===
-{{ac|Incertidumbre en los datos}}
+Misma notación que en el teorema del seno
-Toda medida experimental posee un cierto grado de incertidumbre, proveniente de las limitaciones del aparato de medida o de las condiciones en que se realiza esta. Lo mismo se aplica a toda cantidad derivada de una medida. Por ejemplo, si medimos un periodo con un cronómetro y resulta 3.00&thinsp;s y nos preguntamos por la frecuencia correspondiente es incorrecto decir que ésta es
-<center><math>f = \frac{1}{T}=0.\hat{3}\,\mathrm{Hz}=0.333333\ldots\,\mathrm{Hz}</math></center>
+:<math>a^2 = b^2 + c^2-2bc\cos(\alpha)\,</math>
-ya que esto implica que conoceríamos la frecuencia con infinita precisión, lo cual es imposible. Teniendo en cuenta que hemos dado un periodo con tres cifras, un valor para la frecuencia de 0.333&thinsp;Hz será un resultado más razonable.
+y las correspondientes a los otros dos ángulos.
-Nótese también que hemos indicado el periodo con tres decimales, aunque estos sean cero. Es ésta otra diferencia entre dar una cantidad en Matemáticas y darla en Física. Los dos ceros tras el punto decimal quieren decir que sabemos que el periodo es conocido hasta la centésima de segundo y por tanto los ceros no son superfluos. Este se expresa diciendo que el periodo posee tres ''cifras significativas''.
+==Resolución de triángulos==
+Misma notación que en el teorema del seno y del coseno.
-===Cifras significativas===
+Se trata de dados tres datos (lados o ángulos) hallar los tres restantes.
-El primer factor que nos da información sobre la certidumbre de un dato es el ''número de cifras significativas''. Éstas son las que, como su nombre indica, nos dan información detallada sobre el valor de la cantidad.
+===Dados los tres lados===
+Por el teorema del coseno se determinan los tres ángulos. Para <math>\alpha</math>
-Como regla básica (que luego matizaremos) podemos definirlo como el número de cifras del dato, sin contar los ceros iniciales o finales.
+<center><math>\alpha=\arccos\left(\frac{b^2+c^2-a^2}{2bc}\right)</math></center>
-Veamos algunos ejemplos:
-;2373&thinsp;m: Tiene cuatro cifras significativas.
+y análogamente para los otros dos.
-;12.45&thinsp;V: Tiene también cuatro cifras significativas. La posición del punto decimal es irrelevante. Por ello no hay que confundir el número de cifras significativas con el número de decimales.
-;0.00987&thinsp;s: Tiene tres cifras significativas. Los ceros iniciales nos informan del ''orden de magnitud'' de la cantidad, pero no de su precisión. Esto se ve  más claramente en la ''notación científica'' de un número: 0.00987&thinsp;s = 9.87&times; 10<sup>&minus;3</sup>&thinsp;s.
-;24.50&thinsp;kg;: Tiene cuatro cifras significativas. En este caso, el cero final es una cifra significativa, ya que si no sería superfluo. Por ello, no es lo mismo dar un resultado como 24.50 que darlo como 24.5 ya que la primera forma corresponde a una medida más precisa.
-;45000&thinsp;m: En este caso tenemos una situación ambigua, ya que el número de cifras significativas podría ser 2, 3, 4 o 5, según que los ceros finales aporten información sobre la medida o sólo sobre su orden de magnitud. Esta ambigüedad, de nuevo, desaparece si expresamos el número en notación científica, ya que no es lo mismo 4.5&times;10<sup>4</sup>m  que 4.5000&times;10<sup>4</sup>m.
-El último ejemplo nos muestra que la expresión normal de un número no proporciona suficiente información sobre el número de cifras significativas. Para completar esta información debemos acotar la posible ''incertidumbre'' (o ''error'') de una cantidad.
+===Dados dos lados y el ángulo que abarcan===
+Si conocemos <math>a</math>, <math>b</math> y el ángulo <math>\gamma</math> por el teorema del coseno hallamos <math>c</math>
+<center>
+<math>c=\sqrt{a^2+b^2-2ab\cos(\gamma)}</math></center>
-===Bandas de error===
+una vez conocidos los tres lados podemos aplicar el caso anterior o bien emplear el teorema del seno
-Una forma más completa de expresar la precisión de una medida es con ayuda de las bandas de incertidumbre o bandas de error. Si se ha medido una longitud con una cinta métrica y se se obtiene una medida que está entre las marcas 82&thinsp;mm y 83&thinsp;mm podemos escribir el resultado de la medida como
-<center>x &isin; (82&thinsp;mm,83&thinsp;mm)</center>
+<center><math>\alpha=\mathrm{arcsen}\left(\frac{a}{c}\mathrm{sen}(\gamma)\right)</math></center>
-pero es más práctico adjudicarle un valor a x (usualmente el valor medio, por simplicidad) y expresar el resultado con una cierta banda de error
+===Dados dos lados y otro ángulo===
+Si conocemos <math>a</math>, <math>b</math> y el ángulo <math>\beta</math> por el teorema del seno hallamos <math>\alpha</math>
-<center>x = 82.5&thinsp;&plusmn;&thinsp;0.5&thinsp;mm</center>
+<center><math>\alpha=\mathrm{arcsen}\left(\frac{a}{b}\mathrm{sen}(\beta)\right)</math></center>
-Cuando un resultado se indica de esta forma se quiere decir que la medida tiene una elevada probabilidad (convencionalmente se toma el 95%) de encontrarse en el intervalo indicado. Esta misma incertidumbre se puede expresar de forma compacta, incluyendo al final de la cantidad su incertidumbre, entendiendo que afecta a la última o últimas cifras de la medida, esto es
+y aplicando que los ángulos suman <math>\pi</math>
-<center>x = 82.5(5)&thinsp;mm</center>
+<center><math>\gamma=\pi-\alpha-\beta\,</math></center>
-===Propagación de incertidumbres===
+y a partir de ahí se sigue como en los casos anteriores.
-Cuando partir de una medida experimental directa obtenemos una cierta cantidad calculada a partir de ella, el cálculo lleva aparejado una cierta incertidumbre (lo que se conoce como propagación del error o de la incertidumbre).
-Por ejemplo, imaginemos que queremos hallar la sección de una pieza cilíndrica y tras medir el diámetro concluimos que este se encuentra entre 82&thinsp;mm y 83&thinsp;mm, deducimos que el área  se encontrará entre
+===Dado un lado y dos ángulos===
+Si concemos el lado <math>a</math> y los ángulos <math>\beta</math> y <math>\gamma</math>, hallamos en primer lugar <math>\alpha</math>
-<center><math>A = \frac{\pi D^2}{4}\qquad\Rightarrow\qquad A\in (5281\,\mathrm{mm}^2,5411\,\mathrm{m}^2)</math></center>
+<center><math>\alpha=\pi-\beta-\gamma\,</math></center>
-Vemos en este ejemplo, que la presencia de una incertidumbre limita el número de cifras significativas. No tiene sentido dar el resultado con 8 cifras significativas, si la incertidumbre afecta a la tercera (diga lo que diga la calculadora o el ordenador empleado para calcularla). Por ello, existe un procedimiento sistemático para [[Expresión_de_una_cantidad_con_error._Redondeo|redondear]] una cantidad.
+y luego aplicamos el teorema del seno
-Existe también un [[Incertidumbre_de_una_magnitud_funci%C3%B3n_de_otra%28s%29|procedimiento general]] para determinar la incertidumbre de una función de una o varias variables.
+<center><math>b = a\frac{\mathrm{sen}(\beta)}{\mathrm{sen}(\alpha)}\qquad\qquad c = a\frac{\mathrm{sen}(\gamma)}{\mathrm{sen}(\alpha)}</math></center>
-Todo esto y otros aspectos relacionados con el procedimiento de medida se explica en detalle en la sección de [[Prácticas de laboratorio]].
+===Dados los tres ángulos===
+En ese caso no se pueden dar los tres lados, ya que todos los triángulos semejantes tienen los mismos ángulos independientemente de su tamaño. No obstante, puede darse a proporción entre sus lados mediante el teorema del seno.
-==Problemas==
+[[Categoría:Herramientas matemáticas (GIE)]]
-{{ac|Problemas de metrología (G.I.T.I.)}}
-<categorytree mode=pages depth="2">Problemas de metrología (G.I.T.I.)</categorytree>
-[[Categoría:Metrología (G.I.T.I.)|0]]
-[[Categoría:Física I (G.I.T.I.)|1]]

Buscar

Menú

Perfil