Sistema de tres conductores esféricos

Enunciado

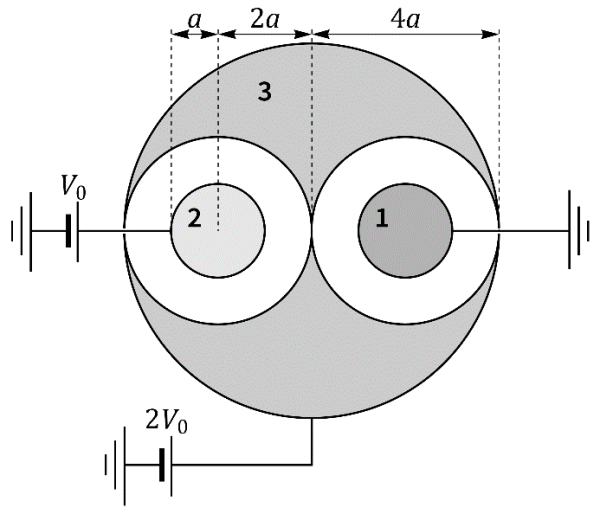
Se tiene un sistema formado por tres conductores metálicos. Dos de ellos (“1” y “2”) son esferas macizas de radio $a=9\,\mathrm {mm}$. El tercero es una esfera de radio $c=4a=36\,\mathrm {mm}$, que tiene dos huecos esféricos de radio $b=2a=18\,\mathrm {mm}$ en cuyo interior se encuentran los conductores “1” y “2”, concéntricamente a cada hueco. El conductor “1” se encuentra conectado a tierra, el “2” a una fuente de tensión de $V_{0}=+1\,\mathrm {kV}$, y el “3” a una de tensión $V_{3}=2V_{0}=2\,\mathrm {kV}$. El infinito se halla a potencial 0 (tierra). No hay más conductores en el sistema. Calcule

1. Las capacidades entre cada par de conductores y de cada uno con el infinito, si las hubiera.
2. La carga neta de cada uno de los 3 conductores.
3. La carga de cada una de las 5 superficies, tanto las exteriores de cada uno como las paredes de los huecos.
4. La energía electrostática almacenada en el sistema.

Capacidades del circuito equivalente

Los conductores 1 y 2 forman con el 3 sendos condensadores esféricos de la misma capacidad

$C_{13}=C_{23}={\frac {4\pi \varepsilon _{0}ab}{b-a}}={\frac {9\times 10^{-3}\times 18\times 10^{-3}}{9\times 10^{9}\times 9\times 10^{-3}}}\,\mathrm {F} =2\,\mathrm {pF}$

Entre el 1 y el 2 no hay ningún condensador, ya que ninguna línea de campo que sale del conductor 1 puede ir a parar al conductor 2. Todas van al 3.

$C_{12}=0\,$

El conductor 1 no forma ningún condensador con el infinito, ya que del 1 solo hay líneas hacia el 3. Lo mismo pasa con el 2.

$C_{11}=C_{22}=0\,$

El conductor 3 sí forma un condensador con el infinito, siendo su capacidad la de un condensador esférico

$C_{33}=4\pi \varepsilon _{0}c={\frac {36\times 10^{-3}}{9\times 10^{9}}}\,\mathrm {F} =4\,\mathrm {pF}$

El circuito está formado entonces por tres condensdores, formando una estrella, más las correspondientes fuentes de tensión.

Carga de cada uno de los conductores

La carga de cada conductor es, en el circuito, igual a la suma de las cargas de los condensadores conectados al nodo correspondiente. Esto da, para el conductor 1

$Q_{1}=C_{13}(V_{1}-V_{3})=2(0-2)\,\mathrm {nC} =-4\,\mathrm {nC}$

Para el 2

$Q_{2}=C_{23}(V_{2}-V_{3})=2(1-2)\,\mathrm {nC} =-2\,\mathrm {nC}$

Para el 3 tenemos tres condensadores

$Q_{3}=C_{13}(V_{3}-V_{1})+C_{23}(V_{3}-V_{2})+C_{33}(V_{3}-0)=\left(2(2-0)+2(2-1)+4(2-0)\right)\,\mathrm {nC} =+14\,\mathrm {nC}$

Carga de cada una de las superficies

Del conductor 1

El conductor 1 tiene una única superficie, por lo que

$Q_{s1}=Q_{1}=-4\,\mathrm {nC}$

Del conductor 2

De la misma manera, tenemos, para el conductor 2

$Q_{s2}=Q_{2}=-2\,\mathrm {nC}$

Del conductor 3

El conductor 3 tiene 3 superficies, una por cada condensador

Superficie enfrentada al conductor 1

En esta pared del hueco, por el teorema de Faraday

$Q_{31}=-Q_{1}=+4\,\mathrm {nC}$

Superficie enfrentada al conductor 2

De nuevo por el teorema de Faraday

$Q_{31}=-Q_{2}=+2\,\mathrm {nC}$

Superficie exterior

Esta superficie contiene el resto de la carga del conductor 3, que es la del condensador que forma con el infinito

$Q_{33}=Q_{3}-Q_{31}-Q_{32}=(14-4-2)\,\mathrm {nC} =+8\,\mathrm {nC}$

Energía almacenada

Podemos calcular la energía almacenada a partir de la fórmula para tres conductores

$U_{\mathrm {e} }={\frac {1}{2}}Q_{1}V_{1}+{\frac {1}{2}}Q_{2}V_{2}+{\frac {1}{2}}Q_{3}V_{3}=\left({\frac {1}{2}}(-4)\cdot 0+{\frac {1}{2}}(-2)\cdot 1+{\frac {1}{2}}(+14)\cdot 2\right)\,\mu \mathrm {J} =13\,\mu \mathrm {J}$