Esfera con hueco esférico

Enunciado

Se tiene una carga $Q=14\,\mathrm {nC}$ distribuida uniformemente en una esfera maciza de radio 10.0 cm en la que se ha horadado una cavidad esférica de radio 5.0 cm cuyo centro está a 5.0 m de la esfera grande.

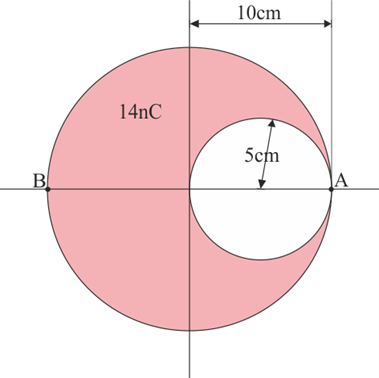
Calcule el campo eléctrico producido por este sistema en los siguientes puntos:

1. O, el centro de la esfera grande.
2. C, el centro del hueco.
3. A, el borde exterior del hueco.
4. B, el punto diametralmente opuesto a A.
5. P, un punto situado a 25 cm del origen O en la dirección de X positivo.

Introducción

Este problema puede hacerse mediante el principio de superposición.

La esfera con hueco equivale a la suma de dos esferas completas: una de radio 2b (siendo $b=5\,\mathrm {cm}$) y densidad de carga positiva y una de radio b con la misma densidad de carga, pero negativa. De etsa manera, en cada elemento de volumen del hueco se superponen la misma cantidad de carga positiva que negativa y el resultado es una densidad de carga nula en esos puntos.

Las cargas de ambas esferas cumplen

$Q_{1}+Q_{2}=Q_{0}\qquad \qquad Q_{1}=-8Q_{2}$

donde la segunda relación sale de que al ser las densidades de carga iguales salvo el signo, la proporción entre las cargas es la misma que entre los volúmenes. Esto nos da las cargas

$Q_{1}={\frac {8}{7}}Q_{0}=16\,\mathrm {nC} \qquad \qquad Q_{2}=-{\frac {1}{7}}Q_{0}=-2\,\mathrm {nC}$

Ahora, para hallar el campo en los diferentes puntos simplemente allicamos superposición y la expresión del campo debido a una esfera cargada uniformemente

${\vec {E}}={\begin{cases}\displaystyle {\frac {Qr}{4\pi \varepsilon _{0}b^{3}}}{\vec {u}}_{r}&r<b\\&\\\displaystyle {\frac {Q}{4\pi \varepsilon _{0}r^{2}}}{\vec {u}}_{r}&r>b\end{cases}}$