Dos superficies esféricas cargadas

Enunciado

Se tiene un sistema formado por dos superficies esféricas cargadas (“1” y “2”), de radios 4b y 2b, respectivamente. La superficie “2” se encuentra parcialmente en el interior de la “1”, centrada a una distancia 3b del centro de la “1”, punto que tomamos como origen de coordenadas. La superficie “1” almacena una carga +Q y la “2” una carga −Q, ambas distribuidas uniformemente sobre cada superficie

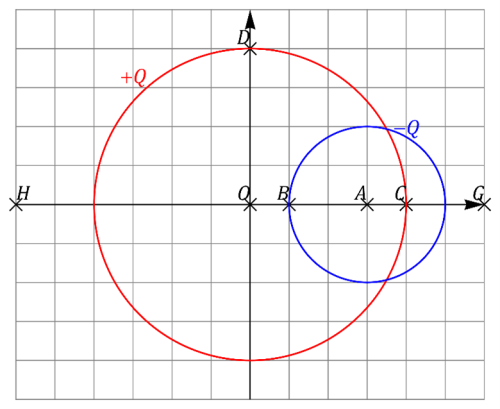
1. Calcule el campo eléctrico en los siguientes puntos del plano OXY:
   1. El origen de coordenadas $O(0,0)$
   2. El centro de la esfera “2” $A(3b,0)$
   3. El punto $B_{1}(b^{-},0)$ situado justo fuera de la esfera “2” y el punto $B_{2}(b^{+},0)$ situado justo dentro de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto?
   4. El punto $C_{1}(4b^{-},0)$ situado justo dentro de la esfera “1” y el punto $C_{2}(4b^{+},0)$ situado justo fuera de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto?
   5. El punto $D_{1}(0,4b^{-})$ situado justo dentro de la esfera “1” y el punto $D_{2}(0,4b^{+})$ situado justo fuera de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto?
2. Calcule el potencial eléctrico en los puntos anteriores, tomando como origen de potencial el infinito.
3. Halle el trabajo necesario para llevar una carga puntual $q_{0}$ desde el punto $G(6b,0)$ al punto $H(-6b,0)$ siguiendo un camino rectilíneo.
4. En puntos alejados del sistema, éste se ve como un dipolo eléctrico. ¿Cuál es el momento dipolar de la distribución?

Campo eléctrico

En cada punto del espacio, el campo eléctrico se puede calcular como la suma del debido a la esfera de carga positiva más el debido a la de carga negativa.

Asimismo, el campo de cada una de ellas en su interior es nulo y en su exterior es como el de una carga puntual con la carga total de la esfera y sutuada en el centro de ésta.

En el punto O

El origen de coordenadas se halla en el interior de la esfera positiva y el exterior de la negativa. Se halla a 3 unidades del centro de esta esfera y en O el vector unitario radial hacia fuera de la esfera es $-{\vec {\imath }}$. Por tanto

Error al representar (función desconocida «\varrepsilon»): {\displaystyle \vec{E}_O=\vec{E}_{O1}+\vec{E}_{O2}=\vec{0}+\frac{4\pi\varepsilon_0}\,\frac{(-Q)}{(3b)^2}(-\vec{\imath}}=\frac{Q}{36\pi\varrepsilon_0 b^2}\vec{\imath}}

En el punto A

El punto A se encuentra en la intersección de ambas esferas y, por tanto, el campo debido a cada una es nulo.

${\vec {E}}_{A}={\vec {E}}_{A1}+{\vec {E}}_{A2}={\vec {0}}+{\vec {0}}={\vec {0}}$

En el punto B

En B₁

Este punto se encuentra, como O, dentro de una esfera y fuera de la otra, pero a una distancia 2b del centro de ésta. Por tanto,

Error al representar (función desconocida «\varrepsilon»): {\displaystyle \vec{E}_{B_1}=\vec{E}_{B_11}+\vec{E}_{B_12}=\vec{0}+\frac{4\pi\varepsilon_0}\,\frac{(-Q)}{(2b)^2}(-\vec{\imath}}=\frac{Q}{16\pi\varrepsilon_0 b^2}\vec{\imath}}

En B₂

Este punto se encuentra, como A, dentro de ambas esferas. Por tanto,

${\vec {E}}_{B_{2}}={\vec {E}}_{B_{2}1}+{\vec {E}}_{B_{2}2}={\vec {0}}+{\vec {0}}={\vec {0}}$

Discontinuidad del campo

Como vemos, en la superfice de la esfera, el campo presenta una discontinuidad igual a

Error al representar (función desconocida «\varrepsilon»): {\displaystyle \vec{E}(B_2) - \vec{E}(B_1) = \vec{0}-\frac{Q}{16\pi\varrepsilon_0 b^2}\vec{\imath} = -\frac{Q}{16\pi\varrepsilon_0 b^2}\vec{\imath}}

Este salto se puede escribir como

Error al representar (función desconocida «\varrepsilon»): {\displaystyle \vec{E}(B_2) - \vec{E}(B_1) = \frac{(-Q)/(4\pi(2b)^2)}{\varrepsilon_0}\vec{\imath}=\frac{\sigma_s}{\varepsilon_0}\vec{\imath}}

siendo $\sigma _{s}$ la densidad superficial de carga de la esfera.