Dos superficies esféricas cargadas

Enunciado

Se tiene un sistema formado por dos superficies esféricas cargadas (“1” y “2”), de radios 4b y 2b, respectivamente. La superficie “2” se encuentra parcialmente en el interior de la “1”, centrada a una distancia 3b del centro de la “1”, punto que tomamos como origen de coordenadas. La superficie “1” almacena una carga +Q y la “2” una carga −Q, ambas distribuidas uniformemente sobre cada superficie

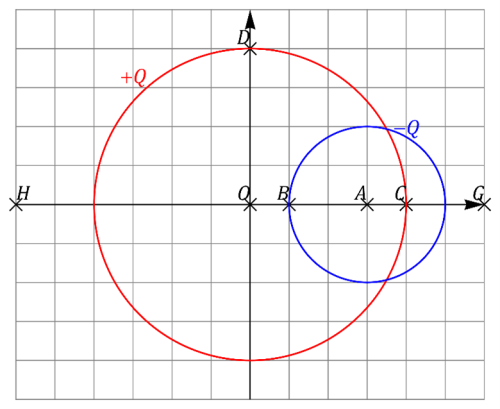
1. Calcule el campo eléctrico en los siguientes puntos del plano OXY:
   1. El origen de coordenadas O(0,0)
   2. El centro de la esfera “2” A(3b,0)
   3. El punto B_1 (b^-,0) situado justo fuera de la esfera “2” y el punto B_2 (b^+,0) situado justo dentro de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto?
   4. El punto C_1 (4b^-,0) situado justo dentro de la esfera “1” y el punto C_2 (4b^+,0) situado justo fuera de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto?
   5. El punto D_1 (0,4b^- ) situado justo dentro de la esfera “1” y el punto D_2 (0,4b^+ ) situado justo fuera de ella. ¿Cuánto vale la discontinuidad en el campo eléctrico en este punto?
2. Calcule el potencial eléctrico en los puntos anteriores, tomando como origen de potencial el infinito.
3. Halle el trabajo necesario para llevar una carga puntual q_0 desde el punto G(6b,0) al punto H(-6b,0) siguiendo un camino rectilíneo.
4. En puntos alejados del sistema, éste se ve como un dipolo eléctrico. ¿Cuál es el momento dipolar de la distribución?