Giro de disco ensartado en varilla

Enunciado

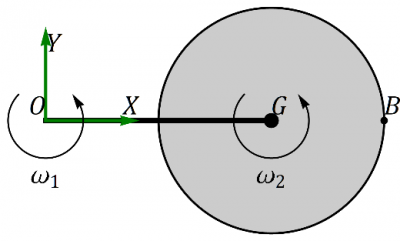
Se tiene una varilla horizontal de masa despreciable y longitud 2R. Un extremo de la varilla se encuentra fijo en el origen de coordenadas, O. La varilla gira en torno al eje OZ con velocidad angular constante ${\vec {\omega }}_{1}=3\omega _{0}{\vec {k}}$. En el otro extremo, G, de la varilla se encuentra ensartado un disco homogéneo de masa m y radio R, también horizontal. El disco gira con velocidad angular constante ${\vec {\omega }}_{2}=2\omega _{0}{\vec {k}}$ alrededor de un eje paralelo a OZ por G. En un momento dado, la varilla se encuentra alineada con el eje OX. Para ese instante…

1. ¿Cuánto vale la velocidad de B, el punto del disco situado en el extremo del disco opuesto a O?
2. ¿Cuánto vale la aceleración de B, el punto del disco situado en el extremo del disco opuesto a O?
3. ¿Dónde se encuentra el centro instantáneo de rotación del disco?
4. ¿Cuánto vale la cantidad de movimiento del disco?
5. ¿Cuánto vale el momento cinético del disco respecto al punto O?
6. ¿Cuánto vale la energía cinética del disco?
7. ¿Cuánto vale la fuerza que se aplica en O para mantener el sistema en movimiento?
8. ¿Cuánto vale el momento resultante que se aplica en O para mantener el sistema en movimiento?

Velocidad de B

Este problema es muy parecido al de dos varillas articuladas, cambiando la segunda varilla por un disco.

Para la velocidad de B aplicamos que podemos hallar en primer lugar la velocidad de G, aplicando que la varilla efectñua un movimiento de rotación alrededor de O

${\vec {v}}_{G}=\omega _{1}{\vec {k}}\times {\overrightarrow {OG}}=3\Omega {\vec {k}}\times (2R{\vec {\imath }})=6\Omega R{\vec {\jmath }}$

Una vez que tenemos la velocidad de G, la usamos para hallar la velocidad de B

${\vec {v}}_{B}={\vec {v}}_{G}+\omega _{2}{\vec {k}}\times {\overrightarrow {GB}}=6\Omega R{\vec {\jmath }}+(2\Omega ){\vec {k}}\times (R{\vec {\imath }})=8\Omega R{\vec {\jmath }}$

Aceleración de B

De manera similar se calcula la aceleración de B. Primero calculamos la de G, que describe un movimiento circular uniforme alrededor del origen

${\vec {a}}_{G}=\overbrace {\alpha _{1}} ^{=0}{\vec {k}}\times {\overrightarrow {OG}}-\omega _{1}^{2}{\overrightarrow {OG}}==-(3\Omega )^{2}(2R{\vec {\imath }})=-18\Omega ^{2}{\vec {\imath }}$

y a partir de la de G hallamos la de B

${\vec {a}}_{B}={\vec {a}}_{G}+\overbrace {\alpha _{2}} ^{=0}{\vec {k}}\times {\overrightarrow {GB}}-\omega _{2}^{2}{\overrightarrow {GB}}=-18\Omega ^{2}{\vec {\imath }}-(2\Omega )^{2}(R{\vec {\imath }})=-22\Omega ^{2}R{\vec {\imath }}$

Centro instantáneo de rotación

Hallamos la posición del CIR del disco a partir de la velocidad de un punto y la velocidad angular del disco

${\overrightarrow {GI}}={\frac {{\vec {k}}\times {\vec {v}}_{G}}{\omega _{2}}}={\frac {{\vec {k}}\times (6\Omega R{\vec {\jmath }})}{2\Omega }}=-3R{\vec {\imath }}$

Esta es la posición respecto a G. Respecto al origen de coordenadas es

${\overrightarrow {OI}}={\overrightarrow {OG}}+{\overrightarrow {GI}}=2R{\vec {\imath }}+(-3R{\vec {\imath }})=-R{\vec {\imath }}$