Enunciado
Se tiene un sistema formado por un recipiente cilíndrico (sólido “1”) con fondo pero sin tapa, de radio y altura 2R. En el interior de este recipiente se encuentra una esfera maciza homogénea (“sólido 2”) de masa m y radio R. Esta esfera se mueve de forma que rueda sin deslizar en todo momento sobre el fondo y la pared. El centro de la bola se mueve en todo momento con rapidez constante  alrededor del eje vertical.
Tomamos un tercer sistema de referencia intermedio “0”, que gira alrededor del eje
alrededor del eje vertical.
Tomamos un tercer sistema de referencia intermedio “0”, que gira alrededor del eje  =OZ_0 de manera que el centro de la esfera siempre se encuentra en el plano
=OZ_0 de manera que el centro de la esfera siempre se encuentra en el plano  . Con ayuda de este sistema determine y exprese:
. Con ayuda de este sistema determine y exprese:
- Las velocidades angulares
 ,
,  y
y 
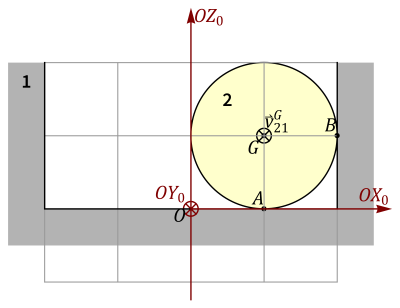
- La posición de los tres ejes instantáneos de rotación (puede ayudarse de la figura)
- Las aceleraciones angulares
 ,
,  y
y 
- Las aceleraciones lineales de los puntos G (centro de la esfera), A (contacto con el fondo) y B (contacto con la pared) de la esfera 2 respecto al sistema de referencia fijo 1.
Velocidades angulares
Arrastre, {01}
El movimiento del sistema “0&” respecto al 1 es una rotación alrededor del eje  . La velocidad angular es de la forma
. La velocidad angular es de la forma

El valor lo obtenemos de que conocemos la velocidad de G

La posición de G en el sistema 0 es, en todo momento,

Por ello, G es un punto fijo en el movimiento relativo.

por lo que

Esto nos da

y

Absoluta, {21}
Relativa, {20}
Ejes instantáneos de rotación
Aceleraciones angulares
Aceleraciones lineales

















