Giro de disco ensartado en varilla

Enunciado

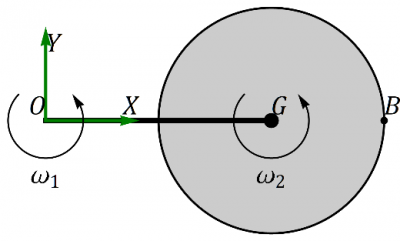
Se tiene una varilla horizontal de masa despreciable y longitud 2R. Un extremo de la varilla se encuentra fijo en el origen de coordenadas, O. La varilla gira en torno al eje OZ con velocidad angular constante ${\vec {\omega }}_{1}=3\Omega {\vec {k}}$. En el otro extremo, G, de la varilla se encuentra ensartado un disco homogéneo de masa m y radio R, también horizontal. El disco gira con velocidad angular constante ${\vec {\omega }}_{2}=2\Omega {\vec {k}}$ alrededor de un eje paralelo a OZ por G. En un momento dado, la varilla se encuentra alineada con el eje OX. Para ese instante…

1. ¿Cuánto vale la velocidad de B, el punto del disco situado en el extremo del disco opuesto a O?
2. ¿Cuánto vale la aceleración de B, el punto del disco situado en el extremo del disco opuesto a O?
3. ¿Dónde se encuentra el centro instantáneo de rotación del disco?
4. ¿Cuánto vale la cantidad de movimiento del disco?
5. ¿Cuánto vale el momento cinético del disco respecto al punto O?
6. ¿Cuánto vale la energía cinética del disco?
7. ¿Cuánto vale la fuerza que se aplica en O para mantener el sistema en movimiento?
8. ¿Cuánto vale el momento resultante que se aplica en O para mantener el sistema en movimiento?

Velocidad de B

Para la velocidad de B aplicamos que podemos hallar en primer lugar la velocidad de G, aplicando que la varilla efectñua un movimiento de rotación alrededor de O

${\vec {v}}_{G}=\omega _{1}{\vec {k}}\times {\overrightarrow {OG}}=3\Omega {\vec {k}}\times (2R{\vec {\imath }})=6\Omega R{\vec {\jmath }}$

Una vez que tenemos la velocidad de G, la usamos para hallar la velocidad de B

${\vec {v}}_{B}={\vec {v}}_{G}+\omega _{2}{\vec {k}}\times {\overrightarrow {GB}}=6\Omega R{\vec {\jmath }}+(2\Omega ){\vec {k}}\times (R{\vec {\imath }})=8\Omega R{\vec {\jmath }}$

Aceleración de B

De manera similar se calcula la aceleración de B. Primero calculamos la de G, que describe un movimiento circular uniforme alrededor del origen

${\vec {a}}_{G}=\overbrace {\alpha _{1}} ^{=0}{\vec {k}}\times {\overrightarrow {OG}}-\omega _{1}^{2}{\overrightarrow {OG}}==-(3\Omega )^{2}(2R{\vec {\imath }})=-18\Omega ^{2}{\vec {\imath }}$

y a partir de la de G hallamos la de B

${\vec {a}}_{B}={\vec {a}}_{G}+\overbrace {\alpha _{2}} ^{=0}{\vec {k}}\times {\overrightarrow {GB}}-\omega _{2}^{2}{\overrightarrow {GB}}=-18\Omega ^{2}{\vec {\imath }}-(2\Omega )^{2}(R{\vec {\imath }})=-22\Omega ^{2}R{\vec {\imath }}$

Centro instantáneo de rotación

Hallamos la posición del CIR del disco a partir de la velocidad de un punto y la velocidad angular del disco

${\overrightarrow {GI}}={\frac {{\vec {k}}\times {\vec {v}}_{G}}{\omega _{2}}}={\frac {{\vec {k}}\times (6\Omega R{\vec {\jmath }})}{2\Omega }}=-3R{\vec {\imath }}$

Esta es la posición respecto a G. Respecto al origen de coordenadas es

${\overrightarrow {OI}}={\overrightarrow {OG}}+{\overrightarrow {GI}}=2R{\vec {\imath }}+(-3R{\vec {\imath }})=-R{\vec {\imath }}$

Cantidad de movimiento del disco

La cantidad de movimiento del sólido la hallamos a partir del movimiento del CM

${\vec {p}}=m{\vec {v}}_{G}=6m\Omega R{\vec {\jmath }}$

Momento cinético respecto a O

Para el momento cinético respecto a O aplicamos el teorema de König

${\vec {L}}_{O}=m{\overrightarrow {OG}}\times {\vec {v}}_{G}+I{\vec {\omega }}_{2}$

El momento de inercia de un disco respecto a un eje perpendicular a él por su centro es

$I={\frac {1}{2}}mR^{2}$

por lo que el momento cinético o angular vale

${\vec {L}}_{O}=m(2R{\vec {\imath }})\times \left(6\Omega R{\vec {\jmath }}\right)+{\frac {1}{2}}mR^{2}\left(2\Omega {\vec {k}}\right)==13mR^{2}\Omega {\vec {k}}$

Este resultado no es el mismo que si calculamos el momento de inercia respecto a O por el teorema de Steiner y luego aplicamos la ecuación $I_{O}{\vec {\omega }}$. La razón es que el punto O no es un punto fijo del disco.

Energía cinética

Para la energía cinética aplicamos su correspondiente teorema de König

$K={\frac {1}{2}}m|{\vec {v}}_{G}|^{2}+{\frac {1}{2}}I\omega _{2}^{2}$

lo quen os da

$K={\frac {1}{2}}m(6\Omega R)^{2}+{\frac {1}{4}}mR^{2}(2\Omega )^{2}=19mR^{2}\Omega ^{2}$

Fuerza aplicada en O

La única fuerza extrna es la que mantiene el sistema en rotación. Por el teorema de la cantidad de movimiento

${\vec {F}}=m{\vec {a}}_{G}=m(-18\Omega ^{2}R{\vec {\imath }})=-18m\Omega ^{2}R{\vec {\imath }}$

Esta fuerza es igual a la tensión de la varilla, que actúa sobre el centro del disco, produciendo un movimiento circular uniforme.

Momento aplicado en O

Para el momento resultante hay que tener mucho cuidado, ya que O no es un punto fijo del disco. En caso de duda debemos calcular el momento respecto al CM

${\vec {M}}_{G}={\frac {\mathrm {d} {\vec {L}}_{G}}{\mathrm {d} t}}={\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\frac {1}{2}}mR^{2}(2\Omega {\vec {k}})\right)={\vec {0}}$

Esta cantidad se anula porque el momento cinético respecto al CM es constante, por serlo la velocidad angular y el momento de inercia.

Para hallar ahora el momento respcto a O, aplicamos la fórmula para cambiar el punto de referencia

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{M}_O=\vec{M}_G+\overrrightarrow{GO}\times\vec{F}= \vec{0}+\left(-2R\vec{\imath}\right)\times \left(-18m\Omega^2R\vec{\imath}\right)=\vec{0}}

Obtenemos que respecto a O también se anula, por estar O en la recta soporte de la fuerza aplicada sobre el sólido.