Diferencia entre revisiones de «Comparación de tres procesos»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 7: | Línea 7: | ||
==Proceso 1== | ==Proceso 1== | ||
Este proceso se compone de un proceso isobárico entre el estado A y uno que llamaremos D, y uno | Este proceso se compone de un proceso isobárico entre el estado A y uno que llamaremos D, y uno isocórico entre D y B. Veremos cada uno por separado. | ||
===Proceso A→D=== | ===Proceso A→D=== | ||
| Línea 37: | Línea 37: | ||
<center><math>W_{A\to B}+Q_{A\to B}=+300\,\mathrm{J}-550\,\mathrm{J}=-250\,\mathrm{J}</math></center> | <center><math>W_{A\to B}+Q_{A\to B}=+300\,\mathrm{J}-550\,\mathrm{J}=-250\,\mathrm{J}</math></center> | ||
==Proceso 2== | |||
Este proceso tiene dos pasos en orden inverso al anterior. Se compone de un proceso isocórico entre el estado A y uno que llamaremos C, y uno isobárico entre D y B. Veremos cada uno por separado. | |||
===Proceso A→C=== | |||
;Trabajo: Al ser un proceso a volumen constante | |||
<center><math>W_{A\to C} = 0\,\mathrm{J}</math></center> | |||
;Calor: Por ser a volumen constante | |||
<center><math>Q_{A\to C}=nc_v(T_C-T_A) = \frac{p_CV_C-p_AV_A}{\gamma-1} = \frac{ V_A(p_B-p_A)}{\gamma-1}=\frac{4\,\mathrm{L}(300-100)\,\mathrm{kPa}}{0.4}= +2000\,\mathrm{J}</math></center> | |||
===Proceso C→B=== | |||
;Trabajo: Al ser un proceso a presión constante | |||
<center><math>W_{C\to B} = -p_B(V_B-V_C) = -p_A(V_B-V_A) = -300\,\mathrm{kPa}(1 - 4)\,\mathrm{L}=+900\,\mathrm{J}</math></center> | |||
;Calor: Por ser a presión constante | |||
<center><math>Q_{C\to B}=nc_p(T_B-T_C) = \frac{\gamma(p_BV_B-p_CV_C)}{\gamma-1} = \frac{\gamma p_B(V_B-V_A)}{\gamma-1}=\frac{1.4}{0.4}300\,\mathrm{kPa}(1 - 4)\,\mathrm{L}= -3150\,\mathrm{J}</math></center> | |||
===Proceso completo=== | |||
Sumando los dos resultados anteriores | |||
<center><math>W_{A\to B}=W_{A\to C}+W_{C\to B}=+0\,\mathrm{J}+900\,\mathrm{J}=+900\,\mathrm{J}</math></center> | |||
<center><math>Q_{A\to B}=Q_{A\to D}+Q_{D\to B}=+2000\,\mathrm{J}-3150\,\mathrm{J}=-1150\,\mathrm{J}</math></center> | |||
y la suma del calor y el trabajo en este proceso es | |||
<center><math>W_{A\to B}+Q_{A\to B}=+900\,\mathrm{J}-1150\,\mathrm{J}=-250\,\mathrm{J}</math></center> | |||
Vemos que el trabajo depende del camino, el calor depende del camino, pero su suma no lo hace, al menos en este ejemplo. Esta es una ley general, conocida como primer principio de la termodinámica. | |||
Esta suma es igual a la diferencia en la energía interna | |||
<center><math>Q + W = \Delta U = -250\,\mathrm{J}</math></center> | |||
==Proceso 3== | |||
El proceso 3 no es ni a presión constante ni a volumen constante, por lo que no podemos emplear ninguna de las dos fórmulas anteriores. No obstante, podemos calcular el trabajo empleando el primer principio de la termodinámica | |||
<center><math>Q = \Delta U - W\,</math></center> | |||
La variación en la energía interna ya la hemos calculado. | |||
<center><math>\Delta U = -250\,\mathrm{J}</math></center> | |||
El trabajo lo podemos hallar a partir de la integral, igual al área bajo la curva. Este área es la de un trapecio | |||
<center><math>W = \frac{p_A+p_B}{2}(V_A-V_B) = 200\,\mathrnm{kPa}(4-1)\mathrm{L}=+600\,\mathrm{J}</math></center> | |||
Por tanto | |||
<center><math>Q = \Delta U - W=-250\,\mathrm{J}-600\,\mathrm{J} = -850\,\mathrm{J}</math></center> | |||
Revisión del 16:53 21 feb 2024
Enunciado
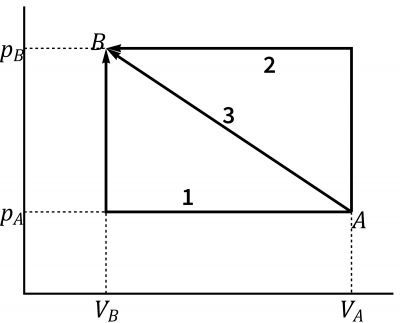
Considere los tres procesos de la figura, con , y , .
- Para los procesos 1 y 2 calcule independientemente el trabajo y el calor que entran en el sistema en cada uno. ¿Cuánto vale la suma del calor y el trabajo en cada uno de los dos procesos?
- Para el proceso 3, calcule el trabajo en este proceso y, a partir de este, el calor que entra en el sistema.
Proceso 1
Este proceso se compone de un proceso isobárico entre el estado A y uno que llamaremos D, y uno isocórico entre D y B. Veremos cada uno por separado.
Proceso A→D
- Trabajo
- Al ser un proceso a presión constante
- Calor
- Por ser a presión constante
Proceso D→B
- Trabajo
- Al ser un proceso a volumen constante
- Calor
- Por ser a volumen constante
Proceso completo
Sumando los dos resultados anteriores
y la suma del calor y el trabajo en este proceso es
Proceso 2
Este proceso tiene dos pasos en orden inverso al anterior. Se compone de un proceso isocórico entre el estado A y uno que llamaremos C, y uno isobárico entre D y B. Veremos cada uno por separado.
Proceso A→C
- Trabajo
- Al ser un proceso a volumen constante
- Calor
- Por ser a volumen constante
Proceso C→B
- Trabajo
- Al ser un proceso a presión constante
- Calor
- Por ser a presión constante
Proceso completo
Sumando los dos resultados anteriores
y la suma del calor y el trabajo en este proceso es
Vemos que el trabajo depende del camino, el calor depende del camino, pero su suma no lo hace, al menos en este ejemplo. Esta es una ley general, conocida como primer principio de la termodinámica.
Esta suma es igual a la diferencia en la energía interna
Proceso 3
El proceso 3 no es ni a presión constante ni a volumen constante, por lo que no podemos emplear ninguna de las dos fórmulas anteriores. No obstante, podemos calcular el trabajo empleando el primer principio de la termodinámica
La variación en la energía interna ya la hemos calculado.
El trabajo lo podemos hallar a partir de la integral, igual al área bajo la curva. Este área es la de un trapecio
Por tanto





















