Doble máquina de Atwood

Enunciado

Se tiene el sistema de dos poleas y tres masas de la figura 5 ($m_{1}=4\,\mathrm {kg}$, $m_{2}=1\,\mathrm {kg}$, $m_{3}=3\,\mathrm {kg}$). Los dos hilos son ideales (inextensibles y sin masa) y las poleas son ideales (sin masa ni fricción). Para este sistema calcule

1. La aceleración de cada una de las masas.
2. La tensión de cada uno de los dos cables.
3. La fuerza que hace el soporte que sujeta el sistema al techo.

Suponga ahora que se sujeta la masa $m_{3}=3\,\mathrm {kg}$, de manera que no puede moverse.

4. ¿Cuál es en ese caso la aceleración de cada una de las otras dos masas?
5. ¿Cuánto vale la tensión de cada cable?
6. ¿Qué fuerza hace el soporte superior y cuál el individuo que sujeta la masa $m_{3}$?

Tome $g=9.8\,\mathrm {m} /\mathrm {s} ^{2}$.

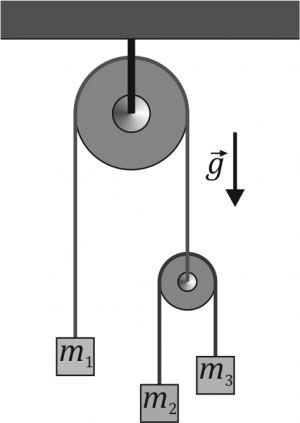
Tensión y aceleraciones

Para cada una de las masas se aplica la segunda ley de Newton

${\begin{array}{rcl}m_{1}a_{1}&=&m_{1}g-F_{T1}\\m_{2}a_{2}&=&m_{2}g-F_{T2}\\m_{3}a_{3}&=&m_{3}g-F_{T3}\end{array}}$

donde hemos medido las distancias desde el centro de la polea superior hacia abajo. En este sistema tenemos 3 ecuaciones, pero 6 incógnitas (las tres aceleraciones y las tres tensiones). Necesitamos tres ecuaciones más.

Para las tensiones tenemos que las masas 2 y 3 están unidas por la misma cuerda, que pasa por una pole ideal (sin masa y sin rozamiento). Por tanto, las dos tensiones son iguales.

$F_{T2}=F_{T3}\,$

Para relacionar la tensión de la masa 1 debemos ver qué le ocurre a la polea que cuelga. Si llamamos “0” a esta polea tenemos

$F_{T1}=F_{T0}\,$

Esta ecuación añade una incógnita adicional. Si observamos que la polea 0 no tiene masa y está sujeta a tres fuerzas (la tensión de un cable que tira hacia arriba y las dos tensiones de otro que tiran hacia abajo se cumple

$-F_{T0}+F_{T2}+F_{T3}=m_{0}a_{0}=0\,$

de donde

$F_{T1}=F_{T2}+F_{T3}=2F_{T2}\,$

Ya tenemos 5 ecuaciones. Queda una sexta, que sale de que los hilos son inextensibles. Por un lado tenemos, para la cuerda superior

$x_{1}+x_{0}=C_{1}\,$

y, para la cuerda inferior,

$(x_{2}-x_{0})+(x_{3}-x_{0})=C_{2}\,$

Podemos eliminar $x_{0}$ de estas dos ecuaciones y llegamos a la ecuación de vínculo

$2x_{1}+x_{2}+x_{3}=2C_{1}+C_{2}=C\,$

Si derivamos esta ecuación dos veces respecto al tiempo obtenemos una relación entre las aceleraciones

$2a_{1}+a_{2}+a_{3}=0\,$

Con esto completamos el sistema de seis ecuaciones con 6 incógnitas

${\begin{array}{rcl}m_{1}a_{1}&=&m_{1}g-F_{T1}\\m_{2}a_{2}&=&m_{2}g-F_{T2}\\m_{3}a_{3}&=&m_{3}g-F_{T3}\\F_{T2}&=&F_{T3}\\F_{T1}&=&2F_{T2}\\0&=&2a_{1}+a_{2}+a_{3}\end{array}}$

Para resolverlo escribimos, en primer lugar, todas las tensiones en función de $F_{T1}$ y despejamos las aceleraciones

${\begin{array}{rcl}a_{1}&=&g-{\dfrac {F_{T1}}{m_{1}}}\\a_{2}&=&g-{\dfrac {F_{T1}}{2m_{2}}}\\a_{3}&=&g-{\dfrac {F_{T1}}{2m_{3}}}\end{array}}$

Ahora combinamos las ecuaciones para que la suma se anule.

$0=2a_{1}+a_{2}+a_{3}=4g-F_{T1}\left({\dfrac {2}{m_{1}}}+{\dfrac {1}{2m_{2}}}+{\dfrac {1}{2m_{3}}}\right)$

De esta ecuación obtenemos la tensión del hilo superior

$F_{T1}=4g\left({\dfrac {2}{m_{1}}}+{\dfrac {1}{2m_{2}}}+{\dfrac {1}{2m_{3}}}\right)^{-1}$

Conocida esta tensión podemos calcular la tensión del otro hilo (que será la mitad) y las aceleraciones de cada una de las masas.

Si damos valores numéricos llegamos a

$F_{T1}=4\cdot 9.8\left({\dfrac {2}{4}}+{\frac {1}{2}}+{\dfrac {1}{6}}\right)^{-1}=33.6\,\mathrm {N}$

La tensión del hilo inferior vale

$F_{T2}={\dfrac {F_{T1}}{2}}=16.8\,\mathrm {N}$

Las aceleraciones de cada una de las masas valen:

$a_{1}=g-{\frac {F_{T1}}{m_{1}}}=9.8-{\frac {33.6}{4}}=+1.4\,{\frac {\mathrm {m} }{\mathrm {s} ^{2}}}$ $a_{2}=g-{\frac {F_{T2}}{m_{2}}}=9.8-{\frac {16.8}{1}}=-7.0\,{\frac {\mathrm {m} }{\mathrm {s} ^{2}}}$ $a_{1}=g-{\frac {F_{T3}}{m_{3}}}=9.8-{\frac {16.8}{3}}=+4.2\,{\frac {\mathrm {m} }{\mathrm {s} ^{2}}}$

Caso de la masa sujeta

Cuando se sujeta la masa 3 es necesario introducir una nueva fuerza actuando sobre esta masa, ya que hay que oponerse a la tensión y al peso que intentan moverla. Al mismo tiempo aparece una nueva ecuación, ya que la masa no se mueve y por tanto $a_{3}=0$. El resto de las ecuaciones no se ve modificada, por lo que el sistema queda ahora en la forma

${\begin{array}{rcl}m_{1}a_{1}&=&m_{1}g-F_{T1}\\m_{2}a_{2}&=&m_{2}g-F_{T2}\\m_{3}a_{3}&=&m_{3}g-F_{T3}+F_{3}\\F_{T2}&=&F_{T3}\\F_{T1}&=&2F_{T2}\\0&=&2a_{1}+a_{2}+a_{3}\\0&=&a_{3}\end{array}}$

Con esto tenemos, para las primeras dos masas

${\begin{array}{rcl}m_{1}a_{1}&=&m_{1}g-F_{T1}\\m_{2}a_{2}&=&m_{2}g-F_{T2}\\F_{T1}&=&2F_{T2}\\0&=&2a_{1}+a_{2}\end{array}}$

Lo resolvemos de la misma manera que en el caso anterior (pero ahora es más simple, pues solo se mueven dos masas)

${\begin{array}{rcl}a_{1}&=&g-{\dfrac {F_{T1}}{m_{1}}}\\a_{2}&=&g-{\dfrac {F_{T1}}{2m_{2}}}\\\end{array}}$

Multiplicando la primera por 2, la segunda por 1 y sumando, queda

$0=2a_{1}+a_{2}=3g-F_{T1}\left({\frac {2}{m_{1}}}+{\frac {1}{2m_{2}}}\right)$

de donde

$F_{T1}=3g\left({\frac {2}{m_{1}}}+{\frac {1}{2m_{2}}}\right)^{-1}$

con el valor

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_{T1}=3\cdot 9.8\cdot(\frac{2}{4}+\frac{1}{2}\right)^{-1} = 29.4\mathrm{N}}

Obsérvese que el valor de la tensión cambia y no es el mismo del apartado anterior.

Una vez que tenemos la tensión hallamos las aceleraciones

Error al representar (error de sintaxis): {\displaystyle a_1 = g -\dfrac{F_{T1}{m_1}=9.8-\frac{29.4}{4}=2.45\,\dfrac{\mathrm{m}}{\mathrm{s}^2}} Error al representar (error de sintaxis): {\displaystyle a_2 = g -\dfrac{F_{T1}{2m_2}=9.8-\frac{29.4}{2}=-4.90\,\dfrac{\mathrm{m}}{\mathrm{s}^2}}

La tensión del segundo cable es

$F_{T2}=F_{T3}={\frac {F_{T1}}{2}}=14.7\mathrm {N}$

y una vez que tenemos la tensión hallamos la fuerza que hay que hacer sobre la masa 3

$F_{3}=F_{T3}-m_{3}g=14.7-29.4=-14.7\,\mathrm {N}$

Por tanto, hay que ejercer una fuerza hacia arriba (recordemos que el eje va hacia abajo) de 14.7 N para que la masa se quede quieta.