Diferencia entre revisiones de «Esfera en recipiente cilíndrico»
(Página creada con «==Enunciado== Se tiene un sistema formado por un recipiente cilíndrico (sólido “1”) con fondo pero sin tapa, de radio y altura 2R. En el interior de este recipiente se encuentra una esfera maciza homogénea (“sólido 2”) de masa m y radio R. Esta esfera se mueve de forma que rueda sin deslizar en todo momento sobre el fondo y la pared. El centro de la bola se mueve en todo momento con rapidez constante <math>v_0</math> alrededor del eje vertical. Tomamos u…») |
Sin resumen de edición |
||
| Línea 8: | Línea 8: | ||
<center>[[Archivo:Esfera-recipiente-cilindrico.png|400px]]</center> | <center>[[Archivo:Esfera-recipiente-cilindrico.png|400px]]</center> | ||
==Velocidades angulares== | ==Velocidades angulares== | ||
===Arrastre, {01}=== | |||
El movimiento del sistema “0&” respecto al 1 es una rotación alrededor del eje <math>OZ_1=OZ_0</math>. La velocidad angular es de la forma | |||
<center><math>\vec{\omega}_{01}=\omega_{01}\vec{k}_0</math></center> | |||
El valor lo obtenemos de que conocemos la velocidad de G | |||
<center><math>\vec{v}^G_{01}=\vec{\omega}_{01}\times\overrightarrow{OG}</math></center> | |||
La posición de G en el sistema 0 es, en todo momento, | |||
<center><math>\overrightarrow{OG}=R\vec{\imath}_0+R\vec{k}_0</math></center> | |||
Por ello, G es un punto fijo en el movimiento relativo. | |||
<center><math>\vec{v}^G_{21}=\overbrace{\vec{v}^G_{20}}^{=\vec{0}}+\vec{v}^G_{01}</math></center> | |||
por lo que | |||
<center><math>\vec{v}^G_{01}= v_0\vec{\jmath}_0</math></center> | |||
Esto nos da | |||
<center><math>v_0\vec{\jmath}_0 = (\omega_{01}\vec{k}_0)\times (R\vec{\imath}_0+R\vec{k}_0) = \omega_{01}R\vec{\jmath}_0</math></center> | |||
y | |||
<center><math>\omega_{01}=\dfrac{v_0}{R}\qquad\qquad \vec{\omega}_{01}=\frac{v_0}{R}\vec{k}_0</math></center> | |||
===Absoluta, {21}=== | |||
===Relativa, {20}=== | |||
==Ejes instantáneos de rotación== | ==Ejes instantáneos de rotación== | ||
==Aceleraciones angulares== | ==Aceleraciones angulares== | ||
==Aceleraciones lineales== | ==Aceleraciones lineales== | ||
Revisión del 11:39 28 nov 2023
Enunciado
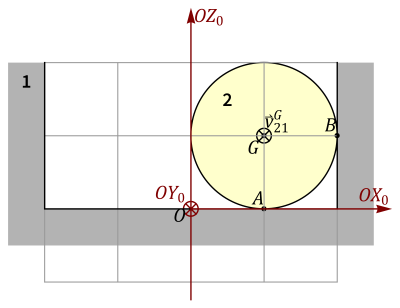
Se tiene un sistema formado por un recipiente cilíndrico (sólido “1”) con fondo pero sin tapa, de radio y altura 2R. En el interior de este recipiente se encuentra una esfera maciza homogénea (“sólido 2”) de masa m y radio R. Esta esfera se mueve de forma que rueda sin deslizar en todo momento sobre el fondo y la pared. El centro de la bola se mueve en todo momento con rapidez constante alrededor del eje vertical. Tomamos un tercer sistema de referencia intermedio “0”, que gira alrededor del eje =OZ_0 de manera que el centro de la esfera siempre se encuentra en el plano . Con ayuda de este sistema determine y exprese:
- Las velocidades angulares , y
- La posición de los tres ejes instantáneos de rotación (puede ayudarse de la figura)
- Las aceleraciones angulares , y
- Las aceleraciones lineales de los puntos G (centro de la esfera), A (contacto con el fondo) y B (contacto con la pared) de la esfera 2 respecto al sistema de referencia fijo 1.
Velocidades angulares
Arrastre, {01}
El movimiento del sistema “0&” respecto al 1 es una rotación alrededor del eje . La velocidad angular es de la forma
El valor lo obtenemos de que conocemos la velocidad de G
La posición de G en el sistema 0 es, en todo momento,
Por ello, G es un punto fijo en el movimiento relativo.
por lo que
Esto nos da
y
















