Diferencia entre revisiones de «Peonza rodante oblicua (CMR)»
(Página creada con «Una peonza está formada por una varilla de longitud <math>\ell=20\,\mathrm{cm}</math> ensartada en un disco de radio <math>R=15\,\mathrm{cm}</math>. Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje <math>OZ_1</math> con rapidez <math>v_0=48\,\mathrm{cm/s}</math>. El disco rueda sin deslizar sobre el plano <math>OX_1Y_1</math>, de manera que en todo ins…») |
Sin resumen de edición |
||
| Línea 1: | Línea 1: | ||
Una peonza está formada por una varilla de longitud <math>\ell=20\,\mathrm{cm}</math> ensartada en un disco de radio <math>R=15\,\mathrm{cm}</math>. Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje <math>OZ_1</math> con rapidez <math>v_0=48\,\mathrm{cm/s}</math>. El disco rueda sin deslizar sobre el plano <math>OX_1Y_1</math>, de manera que en todo instante la velocidad del punto de contacto A es nula. | Una peonza (sólido "3") está formada por una varilla de longitud <math>\ell=20\,\mathrm{cm}</math> ensartada en un disco de radio <math>R=15\,\mathrm{cm}</math>. Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje <math>OZ_1</math> con rapidez <math>v_0=48\,\mathrm{cm/s}</math>. El disco rueda sin deslizar sobre el plano <math>OX_1Y_1</math>, de manera que en todo instante la velocidad del punto de contacto A es nula. | ||
Para este movimiento, determine: | Para este movimiento, determine: | ||
# La velocidad angular del sólido en el movimiento { | # La velocidad angular del sólido en el movimiento {31}. | ||
# La velocidad del punto B, diametralmente opuesto a A, y del punto P situado en <math>25\vec{k}\,\mathrm{cm}</math>, considerado como punto del sólido. | # La velocidad del punto B, diametralmente opuesto a A, y del punto P situado en <math>25\vec{k}\,\mathrm{cm}</math>, considerado como punto del sólido. | ||
# La aceleración angular del sólido. | # La aceleración angular del sólido. | ||
| Línea 8: | Línea 8: | ||
<center>[[Archivo:Peonza-rodante.png|400px]] [[Archivo:Peonza-rodante-b.png]]</center> | <center>[[Archivo:Peonza-rodante.png|400px]] [[Archivo:Peonza-rodante-b.png]]</center> | ||
Sugerencia: Introduzca un sólido intermedio | Sugerencia: Introduzca un sólido intermedio “3” que simplemente gira en torno al eje <math>OZ_1</math>, de manera que el eje <math>OX_2</math> siempre pasa por el O y por el punto de contacto con el suelo. | ||
==Cálculo de la velocidad angular== | |||
===Arrastre, {21}=== | |||
El movimiento {21} es una rotación alrededor del eje <math>OZ_1</math> y, por tanto, su velocidad angular es de la forma | |||
<center><math>\vec{\omega}_{21}=\omega_{21}\vec{k}_2</math></center> | |||
El valor de <math>\omega_{21}</math> lo obtenemos de que G es un punto fijo del sistema 2, siendo su posición en este sistema, en cm, | |||
<center><math>\overrightarrow{OG}=16\vec{\imath}_2+12\vec{k}_2</math></center> | |||
y su velocidad, en cm/s | |||
<center><math>\vec{v}^G_{21}=48\vec{\jmath}_2</math></center> | |||
Debe cumplirse que | |||
<center><math>\vec{v}^G_{21}=\vec{\omega}_{21}\times\overrightarrow{OG}</math></center> | |||
Sustituimos | |||
<center><math>48\vec{\jmath}_2 = \left(\omega_{21}\vec{k}_2\right)\times\left(16\vec{\imath}_2+12\vec{k}_2\right)=16\omega_{21}\vec{\jmath}_2</math></center> | |||
con lo que, en rad/s, | |||
<center><math>\omega_{21}=\frac{48}{16}=3\qquad\qquad \vec{\omega}_{21}=3\vec{k}_2</math></center> | |||
===Relativa, {32}=== | |||
La velocidad angular relativa es la que tiene la peonza alrededor de su eje. La podemos escribir entonces como | |||
<center><math>\vec{\omega}_{32}=\omega_{32}\vec{u}</math></center> | |||
siendo <math>\vec{u}</math> el unitario en la dirección del eje de la peonza. En este caso | |||
<center><math>\vec{\omega}_{32}=\omega_{32}\left(\frac{4}{5}\vec{\imath}_2+\frac{3}{5}\vec{k}_2\right)</math></center> | |||
Para hallar esta velocidad debemos usar el hecho de que la peonza rueda sin deslizar, de manera que la velocidad del punto de contacto de la peonza con el plano es nula en el movimiento absoluto | |||
<center><math>\vec{0}=\vec{v}^A_{31} = \vec{v}^A_{32}+\vec{v}^A_{21}</math></center> | |||
La velocidad de arrastre la calculamos, en cm/s, | |||
<center><math>\vec{v}^A_{21}=\vec{\omega}_{21}\times\overrightarrow{OA}=(3\vec{k}_2)\times(25\vec{\imath}_2)=75\vec{\jmath}_2</math></center> | |||
La relativa se calcula de manera similar | |||
<center><math>\vec{v}^A_{32}=\vec{\omega}_{32}\times \overrightarrow{OA}=\left(\omega_{32}\left(\frac{4}{5}\vec{\imath}_2+\frac{3}{5}\vec{k}_2\right)\right)\times(25\vec{\imath}_2) = 15\omega_{32}\vec{\jmath}_2</math></center> | |||
Puesto que la velocidad angular absoluta debe ser nula, debe cumplirse | |||
<center><math>15\omega_{32}\vec{\jmath}_2 = -75\vec{\jmath}_2 \qquad\Rightarrow\qquad \omega_{32}=-5</math></center> | |||
Y, en forma vectorial, | |||
<center><math>\vec{\omega}_{32}=-5\left(\frac{4}{5}\vec{\imath}_2+\frac{3}{5}\vec{k}_2\right)=-4\vec{\imath}_2-3\vec{k}_2</math></center> | |||
===Absoluta, {31}=== | |||
Una vez que tenemos las velocidades angulares relativa y de arrastre, la absoluta es inmediata: | |||
<center><math>\vec{\omega}_{31}=\vec{\omega}_{32}+\vec{\omega}_{21}=\left(-4\vec{\imath}_2-3\vec{k}_2\right)+\left(3\vec{k}_2\right)=-4\vec{\imath}_2</math></center> | |||
===Procedimiento alternativo=== | |||
Podemos obtener la velocidad angular absoluta directamente observando que si el movimiento {21} es una rotación cuyo eje pasa por O y el movimiento {21} es otra rotación cuyo eje también pasa por O, la composición de ambas es otra rotación cuyo eje también pasa por OA | |||
<center><math>\vec{v}^O_{31}=\vec{v}^O_{32}+\vec{v}^O_{21}=\vec{0}+\vec{0}=\vec{0}</math></center> | |||
Puesto que la velocidad de A en el movimiento {31} es también nula, el eje instantáneo de rotación debe pasar por O y A, con lo que la velocidad angular es de la forma | |||
<center><math>\vec{\omega}_{31}=\omega_{31}\vec{\imath}_2</math></center> | |||
La velocidad que se da en el problema para B vale tanto para el movimiento {21} como para el {31} | |||
<center><math>\vec{v}^G_{31}=48\vec{\jmath}_2</math></center> | |||
Debe cumplirse que | |||
<center><math>\vec{v}^G_{31}=\vec{\omega}_{31}\times\overrightarrow{OG}</math></center> | |||
Sustituimos | |||
<center><math>48\vec{\jmath}_2 = \left(\omega_{31}\vec{\imath}_2\right)\times\left(16\vec{\imath}_2+12\vec{k}_2\right)=-12\omega_{21}\vec{\jmath}_2</math></center> | |||
con lo que, en rad/s, | |||
<center><math>\omega_{31}=-\frac{48}{12}=-4\qquad\qquad \vec{\omega}_{31}=-4\vec{\imath}_2</math></center> | |||
Revisión del 17:09 25 nov 2023
Una peonza (sólido "3") está formada por una varilla de longitud ensartada en un disco de radio . Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje con rapidez . El disco rueda sin deslizar sobre el plano , de manera que en todo instante la velocidad del punto de contacto A es nula. Para este movimiento, determine:
- La velocidad angular del sólido en el movimiento {31}.
- La velocidad del punto B, diametralmente opuesto a A, y del punto P situado en , considerado como punto del sólido.
- La aceleración angular del sólido.
- La aceleración de los puntos A, G, B, O y P, considerados como puntos del sólido.
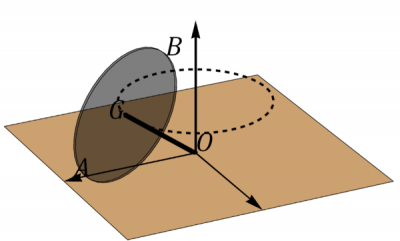
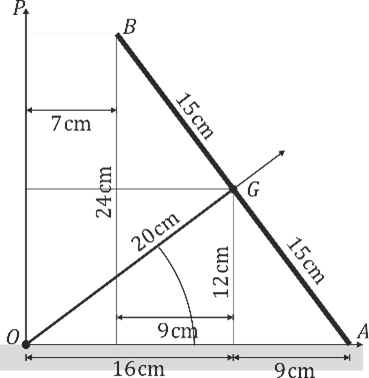
Sugerencia: Introduzca un sólido intermedio “3” que simplemente gira en torno al eje , de manera que el eje siempre pasa por el O y por el punto de contacto con el suelo.
Cálculo de la velocidad angular
Arrastre, {21}
El movimiento {21} es una rotación alrededor del eje y, por tanto, su velocidad angular es de la forma
El valor de lo obtenemos de que G es un punto fijo del sistema 2, siendo su posición en este sistema, en cm,
y su velocidad, en cm/s
Debe cumplirse que
Sustituimos
con lo que, en rad/s,
Relativa, {32}
La velocidad angular relativa es la que tiene la peonza alrededor de su eje. La podemos escribir entonces como
siendo el unitario en la dirección del eje de la peonza. En este caso
Para hallar esta velocidad debemos usar el hecho de que la peonza rueda sin deslizar, de manera que la velocidad del punto de contacto de la peonza con el plano es nula en el movimiento absoluto
La velocidad de arrastre la calculamos, en cm/s,
La relativa se calcula de manera similar
Puesto que la velocidad angular absoluta debe ser nula, debe cumplirse
Y, en forma vectorial,
Absoluta, {31}
Una vez que tenemos las velocidades angulares relativa y de arrastre, la absoluta es inmediata:
Procedimiento alternativo
Podemos obtener la velocidad angular absoluta directamente observando que si el movimiento {21} es una rotación cuyo eje pasa por O y el movimiento {21} es otra rotación cuyo eje también pasa por O, la composición de ambas es otra rotación cuyo eje también pasa por OA
Puesto que la velocidad de A en el movimiento {31} es también nula, el eje instantáneo de rotación debe pasar por O y A, con lo que la velocidad angular es de la forma
La velocidad que se da en el problema para B vale tanto para el movimiento {21} como para el {31}
Debe cumplirse que
Sustituimos
con lo que, en rad/s,




























