Diferencia entre revisiones de «Doble máquina de Atwood»
Secciones
(Página creada con «==Enunciado== Se tiene el sistema de dos poleas y tres masas de la figura 5 (<math>m_1=4\,\mathrm{kg}</math>, <math>m_2=1\,\mathrm{kg}</math>, <math>m_3=3\,\mathrm{kg}</math>). Los dos hilos son ideales (inextensibles y sin masa) y las poleas son ideales (sin masa ni fricción). Para este sistema calcule # La aceleración de cada una de las masas. # La tensión de cada uno de los dos cables. # La fuerza que hace el soporte que sujeta el sistema al techo. Suponga ahora…») |
Sin resumen de edición |
||
| Línea 15: | Línea 15: | ||
==Tensión y aceleraciones== | ==Tensión y aceleraciones== | ||
Para cada una de las masas se aplica la segunda ley de Newton | |||
<center><math>\begin{array}{rcl} | |||
m_1a_1&=&m_1 g - F_{T1}\\ | |||
m_2a_2&=&m_2 g - F_{T2}\\ | |||
m_3a_3&=&m_3 g - F_{T3} | |||
\end{array}</math></center> | |||
donde hemos medido las distancias desde el centro de la polea superior hacia abajo. En este sistema tenemos 3 ecuaciones, pero 6 incógnitas (las tres aceleraciones y las tres tensiones). Necesitamos tres ecuaciones más. | |||
Para las tensiones tenemos que las masas 2 y 3 están unidas por la misma cuerda, que pasa por una pole ideal (sin masa y sin rozamiento). Por tanto, las dos tensiones son iguales. | |||
<center><math>F_{T2}=F_{T3}\,</math></center> | |||
Para relacionar la tensión de la masa 1 debemos ver qué le ocurre a la polea que cuelga. Si llamamos “0” a esta polea tenemos | |||
<center><math>F_{T1}=F_{T0}\,</math></center> | |||
Esta ecuación añade una incógnita adicional. Si observamos que la polea 0 no tiene masa y está sujeta a tres fuerzas (la tensión de un cable que tira hacia arriba y las dos tensiones de otro que tiran hacia abajo se cumple | |||
<center><math>-F_{T0}+F_{T2}+F_{T3}=m_0 a_0=0\,</math></center> | |||
de donde | |||
<center><math>F_{T1}=F_{T2}+F_{T3}=2F_{T2}\,</math></center> | |||
Ya tenemos 5 ecuaciones. Queda una sexta, que sale de que los hilos son inextensibles. Por un lado tnemos, de la cuerda superior | |||
<center><math>x_1+x_0=C_1\,</math></center> | |||
y, para la cuerda inferior, | |||
<center><math>(x_2-x_0)+(x_3-x_0) = C_2</math></center> | |||
Revisión del 18:44 13 nov 2023
Enunciado
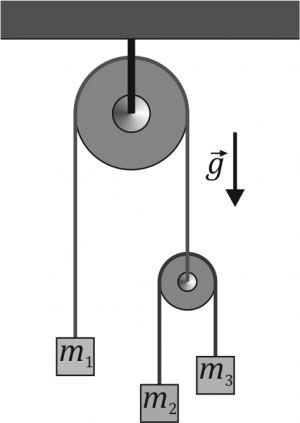
Se tiene el sistema de dos poleas y tres masas de la figura 5 (, , ). Los dos hilos son ideales (inextensibles y sin masa) y las poleas son ideales (sin masa ni fricción). Para este sistema calcule
- La aceleración de cada una de las masas.
- La tensión de cada uno de los dos cables.
- La fuerza que hace el soporte que sujeta el sistema al techo.
Suponga ahora que se sujeta la masa , de manera que no puede moverse.
- ¿Cuál es en ese caso la aceleración de cada una de las otras dos masas?
- ¿Cuánto vale la tensión de cada cable?
- ¿Qué fuerza hace el soporte superior y cuál el individuo que sujeta la masa ?
Tome .
Tensión y aceleraciones
Para cada una de las masas se aplica la segunda ley de Newton
donde hemos medido las distancias desde el centro de la polea superior hacia abajo. En este sistema tenemos 3 ecuaciones, pero 6 incógnitas (las tres aceleraciones y las tres tensiones). Necesitamos tres ecuaciones más.
Para las tensiones tenemos que las masas 2 y 3 están unidas por la misma cuerda, que pasa por una pole ideal (sin masa y sin rozamiento). Por tanto, las dos tensiones son iguales.
Para relacionar la tensión de la masa 1 debemos ver qué le ocurre a la polea que cuelga. Si llamamos “0” a esta polea tenemos
Esta ecuación añade una incógnita adicional. Si observamos que la polea 0 no tiene masa y está sujeta a tres fuerzas (la tensión de un cable que tira hacia arriba y las dos tensiones de otro que tiran hacia abajo se cumple
de donde
Ya tenemos 5 ecuaciones. Queda una sexta, que sale de que los hilos son inextensibles. Por un lado tnemos, de la cuerda superior
y, para la cuerda inferior,











